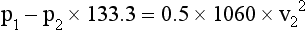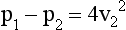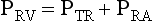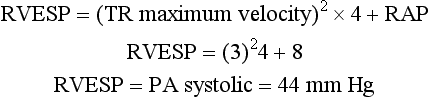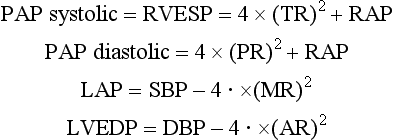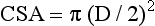4
Principles and Physics
Equations to Remember (the Bernoulli Equation, Velocity-Time Integrals, and the Continuity Equation)
 The Bernoulli Equation
The Bernoulli Equation
These relationships have been described by Bernoulli as:
where
p1 = the pressure proximal to the obstruction
p2 = the pressure distal to the obstruction
p1 − p2 = the pressure difference over the obstruction
v1 = the velocity proximal to the obstruction
v2 = the velocity distal to the obstruction
ρ= the density of blood, which is equal to approximately 1060 kg/m 3
∫(dv/dt)ds = the integral of the blood flow acceleration over a given distance
R(µ) = the resistance, R, as a function of blood viscosity, µ
Thus, p1 − p2 = 3.976 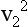 , and the clinically relevant simplified Bernoulli equation is:
, and the clinically relevant simplified Bernoulli equation is:
With this formula, the pressure gradient across a fixed orifice can be approximated. It may be applied to the measurement of intravascular pressures as well as the gradient across a stenotic orifice.
 Determination of Intravascular Pressures
Determination of Intravascular Pressures
The Bernoulli equation may be used to estimate intracardiac pressures. By measuring retrograde flow velocity through a regurgitant valve, transvalvular pressures during systole may be determined, allowing for estimation of intracardiac pressures. For example, the maximum velocity of the tricuspid regurgitation (TR) jet reflects the pressure drop across a regurgitant tricuspid valve (PTR), which is the systolic pressure difference between the right ventricle (RV) and right atrium (RA). RV systolic pressure can be obtained by adding an estimated or measured RA pressure (RAP) to the systolic pressure gradient across the tricuspid valve during systole. Assuming there is some degree of tricuspid regurgitation (TR), the peak blood flow velocity during systole across the tricuspid valve may be measured using continuous wave Doppler (CWD), as described in Chapter 3. The pressure gradient across the tricuspid valve may be calculated using the simplified Bernoulli equation (Equation 4-2). If this value is added to the estimated or measured RA pressure, the RV end-systolic pressure (RVESP) may be measured. In the absence of right ventricular outflow tract obstruction, pulmonary artery (PA) systolic pressure will be the same as RVESP. For example,
If TR velocity = 3.0 m/s and RAP = 8 mm Hg, then:
Similarly, pulmonary regurgitation (PR) velocity represents the diastolic pressure difference between the PA and the RV. Therefore, PA diastolic pressure = RV end-diastolic pressure (RVEDP) + 4 × (PR end-diastolic velocity) 2, assuming that RVEDP is equal to RAP (estimated or measured). Similarly, mitral regurgitation (MR) jet velocity represents the systolic pressure difference between the left ventricle (LV) and the left atrium (LA). In patients without LVOT obstruction or aortic stenosis, systolic blood pressure (SBP) is essentially equal to LV systolic pressure; therefore, LAP is equal to SBP − 4 · × (MR) 2. Finally, aortic regurgitation (AR) velocity reflects the diastolic pressure gradient between the aorta and the LV. In summary:
Stevenson compared six different echocardiographic techniques to measure PA pressure. 1 When compared with direct measurements, some of these techniques yielded highly accurate correlations (r = 0.97), but they were not applicable in all patients.
 Doppler Measurements of Flow: Velocity-Time Integral (VTI)
Doppler Measurements of Flow: Velocity-Time Integral (VTI)
In addition to measuring gradients, the measurements of blood flow velocity may be used to estimate flow within a given structure. The derivative of a function is the slope of the curve at a given point, while an integral of a function is the area under the curve between two points along its x-axis. Given an equation that would describe distance transversed, the time derivative or slope at any given point would represent its velocity; the time derivative of the velocity at any given point would be its acceleration ( Fig. 4-1). Similarly, given a graph of acceleration versus time, the integral would yield a velocity measurement; the integral of a velocity-versus-time graph would yield a distance traversed. A CWD velocity profile is a display of velocity versus time. If one integrates this velocity profile between two time points (i.e., calculates the area under the curve), the distance traversed of “a region of blood” flowing during this period may be estimated. Since flow velocity is not constant throughout a flow cycle, all of the flow velocities during the entire ejection period is integrated to measure “distance traversed” of this “region of blood.” This integration of flow velocities in a given period of time is called the velocity-time integral (VTI) and yields length or distance (in centimeters [cm] or meters [m]). When flows at a particular location along the LVOT or aorta are required (i.e., spacial specificity is necessary), PWD should be used, provided the velocity does not exceed the PW Nyquist limit. High pulse repetition frequency (HPRF) may also be used. Multiple “ROI” points may be seen indicating range ambiguity of the cursor. If the velocities are too high, it is not possible to localize the jet without assumptions.

Figure 4-1 Relationship among distance, velocity, and acceleration. Derivative of function of position versus time results in its velocity; derivative of velocity at any given point would be its acceleration. Conversely, the integral of acceleration over time is velocity, and the integral of velocity over time is distance traversed. This is a Doppler spectral display of velocity versus time. Integrating this spectrum between two time points (i.e., calculating the area under the curve), distance traversed during this period may be calculated.
where D
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


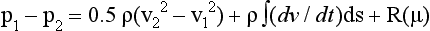
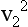 ).
).