The conventional analysis of a typical clinical trial focuses on the time to occurrence of the first among a composite set of alternative events such as death or nonfatal myocardial infarction. Subsequent recurrent events are thereby excluded from consideration to ensure that all the observations were mutually exclusive of each other. Thus, not all events occurring during follow-up will be analyzed. Consequently, some investigators are now reporting additional analyses of previously published trials based on a naive comparison of the total number of events—first events plus recurrent events—and are recommending that these additional analyses be routinely conducted in future trials. We have summarized the potential limitations of this proposal and suggest other methods to analyze recurrent events, with a particular focus on kinetic modeling. The application of this approach to several previously published trials illustrates its facility to help elucidate the causal mechanisms underlying empirical demonstrations of safety and efficacy.
The typical randomized clinical trial assesses the first among a composite set of component end points (e.g., major adverse cardiovascular events) as the primary outcome of interest. According to this “first things first” strategy, once a patient experiences an initial event (any of the components), recurrent events (subsequent components) are excluded from consideration to ensure that all the outcomes are mutually exclusive of each other, as required for the conventional assessment of statistical significance. Thus, none of these so-called recurrent events will be analyzed.
At the very least, exclusion of this “forbidden fruit” clearly denies us the opportunity to assess the safety and efficacy of the treatment relative to the recurrent events. In addition, by reducing the operative event rate, it necessitates an increase in the size and cost of the trial. Accordingly, some investigators have proposed we analyze, not only the first events, but also the total number of events—first events plus recurrent events. Although this “all things considered” strategy might suffice when the number of recurrences is the primary outcome of interest (e.g., anginal episodes), it can falsely inflate the count for the typical composite outcome. Its adoption could thereby lead to additional type I errors (adjudging a treatment safe and/or efficacious when, in fact, it is not). Our goal was to outline the basis for these concerns and propose several, more fruitful approaches to the analysis of recurrent events.
The essential difficulty is that total events—unlike first events—are not mutually exclusive of each other. Take a common composite outcome (death or nonfatal infarction) as an example. Patients can transition from the antecedent event-free state (A) to the consequent outcome states—nonfatal infarction (B) or death (C) —by a pair of alternative paths. Along the parallel path, the transitions are simultaneous, such that A → B and A → C (with the arrows indicating the course of each transition). In this case, the component outcomes are mutually exclusive (their joint occurrence B and C = 0), and an analysis based on total events ( B + C ) will thereby lead to the same conclusion as that based on the first events. Along the serial path, however, the transitions are consecutive, such that A → B → C . In this case, the components are not mutually exclusive ( B and C > 0), and a count of total events will falsely inflate the event rate—by as much as a doubling—leading to potentially erroneous statistical conclusions. If exclusivity among the transitions were the norm and nonexclusivity were the exception, we might argue that the benefit associated with the additive analysis of total events would outweigh the harm associated with the overcounting of events. However, in the real world, just the opposite is the case. Patients who experience some events (e.g., nonfatal infarction) are all the more likely to experience additional events (e.g., postinfarction death).
Fortunately, there are better ways to squeeze the juice from this “forbidden fruit.” The most methodical strategy would be to itemize all the “trees-of-the-garden,” note the location of all the fruits (first events and recurrent events), and the time it took each to ripen, identify the prunings omitted from the harvest, and include all these details in the written report. This would allow informed consumers to confirm the accuracy of the official tally, or to perform additional tallies of their own without double counting any of the crops. Investigators are likely to resist this proposal, however, as it could encourage a fruit salad of post hoc analyses that might confuse (or even mislead) a less informed consumer.
A more rigorous strategy would revise the trial’s design and redefine “first events” as an entry criterion rather than an outcome. This would allow us to randomize patients to treatment after the first event and to analyze the previously excluded second event in the standard manner—analysis of event n +1 requiring randomization after event n . However, as a consequence, we could no longer assess the impact of treatment on the first events. In effect, we will have excluded the good plums instead of the bad apples.
A more robust strategy would use any of the many stochastic models specifically adapted to the assessment of recurrent events—a fertile field of current biostatistical research. The mathematical complexity of these stochastic models, however, can be intimidating to the typical clinician. In contrast, kinetic models used to describe the time course of chemical reactions or the spread of epidemic infections can be far less intimidating, because they portray the direct causative mechanisms resulting in the outcome events, rather than the indirect statistical associations among them. We shall outline the general construction of these models and illustrate their practical utility by application to a few representative clinical trials.
Kinetic Modeling of Clinical Trial Outcomes
In principle, we can construct a kinetic model for an outcome with any degree of complexity (any number of recurrences of any number of components in any order of appearance). For simplicity, however, we shall restrict ourselves to a hybrid of the parallel and serial transitions in our earlier example:
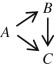
The canonical form of these transitions is that of a first-order exponential decay, ( S ) = e −kt , by which the change in state S relative to time t (risk) is inversely proportional to its prevalence ( S ), such that d ( S )/ dt = − k ( S ), where k is a constant of proportionality representing the change in risk relative to time (hazard). These epidemiological constructs are direct analogs of those for classic mechanical dynamics ( Table 1 ).
| Mechanical Analog | Mathematical Definition | Epidemiologic Analog |
|---|---|---|
| Position | x | Prevalence |
| Velocity | y=ⅆxⅆt y = ⅆ x ⅆ t | Risk |
| Acceleration | z=ⅆyⅆt z = ⅆ y ⅆ t | Hazard |
The risk associated with each state transition in this hybrid model is thereby expressed as a linear differential equation characterizing the rates of appearance minus the rates of disappearance:
Integrating these so-called hazard functions relative to time gives us a set of exponential equations describing the prevalence of each state over time in terms of the associated rate constants:
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


