Introduction

Although large effects on survival arising from certain treatments may occasionally be obvious from simple observation (as, for example, when cardioversion for ventricular fibrillation avoids otherwise certain death), the vast majority of interventions have only moderate effects on major outcomes and hence are impossible to evaluate without careful study. Unfortunately, enthusiasm for the biologic foundations of a particular therapeutic approach often leads to exaggerated hopes for the effects of treatment on major clinical outcomes. These hopes may be based on dramatic laboratory measures of efficacy or on the types of surrogate outcome that are commonly studied before drugs go into Phase III or IV studies; for example, a drug may almost completely prevent experimental ischemia progressing to infarction or practically abolish experimental thrombosis. However, these large effects on surrogate end-points very rarely translate into large effects on major clinical outcomes; the overwhelming message from over three decades of clinical trials in cardiology is that the net effects of most treatments are typically moderate in size. This chapter explains why large-scale randomized evidence, either in a single “mega-trial” or in a meta-analysis of similar trials, is generally an absolute requirement if such moderate effects on major outcomes are to be characterized reliably.

It is important to appreciate that progress in cardiologic practice, and in the prevention of cardiovascular disease, has been and remains dependent on the availability of large-scale randomized trials and of appropriately large-scale meta-analyses of such trials. In the management and prevention of acute myocardial infarction (MI), for example, these methods have helped to demonstrate that fibrinolytic therapy,^1–4 aspirin,^2,4,5 blood pressure-lowering treatments,⁶ and statins^7,8 all produce net benefits which, although individually moderate in size, have together produced a substantial improvement in the prognosis of acute MI. Similarly, the demonstration that angiotensin-converting enzyme (ACE) inhibitors and beta-blockers produce moderate reductions in the risk of death, cardiovascular disease and rates of hospitalization for worsening heart failure^9,10 has improved the outcome of patients with chronic heart failure.

Clinical trials: minimizing biases and random errors

Any clinical study whose main objective is to assess moderate treatment effects must ensure that any biases and any random errors that are inherent in its design are both substantially smaller than the effect to be measured.¹¹ Biases in the assessment of treatment can be produced by differences between randomized arms in factors other than the treatment under consideration. Observational (that is, non-randomized) studies, in which the outcome is compared between individuals who received the treatment of interest and those who did not, can be subject to large biases.¹² Avoidance of biases can only be guaranteed by proper randomized allocation of treatment, blinded outcome assessment and appropriate statistical analysis, with no unduly data-dependent emphasis on specific subsets of the overall evidence (Box 3.1).^11,13

Avoidance of moderate biases

Proper randomization to prevent foreknowledge of treatment allocation

The fundamental reason for random allocation of treatment in clinical trials is to maximize the likelihood that each type of patient will have been allocated in similar proportions to the different treatment strategies being investigated.¹⁴ A key requirement is that treatment allocation should be concealed at the point of randomization since, if the next treatment allocation can be deduced by those entering patients, decisions about whether to enter a patient may be affected and, as a result, those allocated one treatment might differ systematically from those allocated another.¹⁵ For example, in the Captopril Prevention Project (CAPPP) trial,¹⁶ envelopes containing the antihypertensive treatment allocation could be opened before patients were irreversibly entered into the study. Highly significant differences in pre-entry blood pressure between the treatment groups, which were too large to have been due to chance, may well have been the result of this design weakness.¹⁷ Proper randomization therefore requires that trial procedures are organized in a way that ensures that the decision to enter a patient is made irreversibly and without knowledge of the trial treatment to which a patient will be allocated. Once randomized, it is also generally desirable to “blind” both the patient and their doctor (whenever feasible) to the allocated treatment, for reasons discussed below.

Blinding of treatment allocation and of outcome assessment

While randomization should ensure a valid, i.e. unbiased, assessment of the effectiveness of a study drug, substantial bias can still be introduced if there is the potential for subjective judgment in the reporting, evaluation or data processing of clinical events (particularly when such judgments are made with knowledge, or suspected knowledge, of the treatment allocation) or if patients or their doctors are themselves aware of the treatment to which they have been randomized (since their subsequent healthcare and health behaviors may differ systematically from the comparison group in a way that influences clinical outcomes). Patients (and their doctors) should therefore be blinded to the randomized treatment wherever possible and, critically, study outcomes should be evaluated by people who are unaware of the allocated treatment.

Of course, some drugs may produce characteristic side effects which cannot effectively be hidden from a doctor or, indeed, from a well-informed patient. In some types of trials it may be impossible to blind a patient to the treatment received (e.g. surgical intervention trials). Moreover, even when blinding of patients and doctors is theoretically possible, in some circumstances it could act as a barrier to the practical feasibility of the study through the introduction of unnecessary complications and cost (for instance, in a trial where the doses of different study drugs need to be adjusted during the follow-up period). To overcome such problems, PROBE¹⁸ (Prospective Randomized Open-label Blinded Endpoint) study designs are increasingly being employed (e.g. in the Anglo-Scandinavian Cardiac Outcomes Trial (ASCOT)¹⁹ and the Incremental Decrease in Endpoints through Aggressive Lipid lowering (IDEAL) study²⁰). The key feature of a PROBE design is that patients are aware of the study medication to which they have been randomized, as are their doctors. (It is important to note that, while patients and their doctors are unblinded to treatment allocation in a PROBE trial, it remains critically important that randomization procedures prevent foreknowledge of the next treatment to be allocated, and that outcome assessors are blinded to study allocation.) A potential for bias exists, however, if knowledge of a patient’s study medication results in any differential reporting of study outcomes by study staff or differential use of concomitant drugs. This can be largely mitigated by the use of clearly defined and verifiable outcomes, blinded outcome adjudication and various means of evaluation of all or a random subset of patients to assess whether events have been missed, and whether any “missingness” is differential. The potential advantages of PROBE designs include their reduced cost and their similarity to standard clinical practice. However, it is important that these benefits are not achieved at the expense of moderate biases in estimates of treatment effects.

Intention-to-treat analyses

Even when studies have been properly randomized and blinded, moderate biases can still be introduced by inappropriate analysis or interpretation. This can happen, for example, if patients are excluded after randomization, particularly when the prognosis of the excluded patients in one treatment group differs from that in the other (such as might occur, for example, if non-compliant participants were excluded after randomization). This point is well illustrated by the Coronary Drug Project,²¹ which compared clofibrate versus placebo among around 5000 patients with a history of coronary heart disease. In this study, patients who took at least 80% of their allocated clofibrate (“good compliers”) had substantially lower five-year mortality than “poor compliers”, who did not (15.0% vs 24.6% respectively; P = 0.0001). However, there was a similar difference in outcome between good and poor compliers in the placebo group (15.1% vs 28.3%; P < 0.00001), suggesting that good and poor compliers were prognostically different even after allowing for any benefits of actually taking clofibrate.²¹ Under the null hypothesis of no treatment effect, the least biased assessment of the treatment effect is that which compares all those allocated to one treatment versus all those allocated to the other (that is, an “intention-to-treat” analysis), irrespective of what treatment they actually received.²²

Because some degree of non-compliance with allocated treatments may be unavoidable in randomized trials, intention-to-treat analyses will tend to underestimate the effects produced by full compliance. However, “on treatment” (or “per protocol”) analyses, which estimate treatment effects through analyses of compliant patients, are potentially biased; it is more appropriate to calculate an “adjustment” based on the level of compliance and then to apply this to the estimate of the treatment effect provided by the intention-to-treat comparison.²³ For example, in a meta-analysis of the randomized trials of prolonged use of antiplatelet therapy among patients with occlusive vascular disease, the average compliance one year after treatment allocation seemed to be around 80%.²⁴ Application of this estimate of compliance to the proportional reduction of about 30% in non-fatal MI and stroke estimated from intention-to-treat analyses of these trials suggests that full compliance with antiplatelet therapy might produce reductions in risk of about 35–40%.

Inappropriate use and interpretation of subgroup analyses

In the medical literature a particularly important source of bias is unduly data-dependent emphasis on selected trials or on particular subgroups of patients. Such emphasis is often entirely inadvertent, arising from a perfectly reasonable desire to understand the randomized trial results in terms of who to treat, which treatments to prefer or disease mechanisms. However, whatever its origins, selective emphasis on particular parts of the evidence can often lead to seriously misleading conclusions. This is because the identification of categories of patients for whom treatment is particularly effective (or ineffective) requires surprisingly large quantities of data. Even if the real sizes of the treatment effects do vary substantially among subgroups of patients, subgroup analyses are so statistically insensitive that they may well fail to demonstrate these differences. On the other hand, if the real proportional risk reductions are about the same for everybody, subgroup analyses can vary so widely just by the play of chance that the results in selected subgroups may be exaggerated. Indeed, it can be shown that if an overall treatment effect is conventionally statistically significant at the 5% level (i.e. P = 0.05), and patients are randomly split into two equal-sized groups, then there is a 1 in 3 chance that there will be a statistically significant treatment effect in one group and a non-significant effect in the other.²⁵ Thus, even when significant “interactions” are found, they may be a poor guide to the sizes (and even the directions) of any genuine differences, owing more to chance than to reality.

However, even if true differences in the effect of a treatment do exist between different groups of patients, then under certain circumstances, the overall treatment effect can still provide a better estimator of the effect in any given subgroup than the estimate actually derived from that subgroup (the mathematical theory of James-Stein estimators provides formal mathematical support for this).²⁶ The logical basis for placing emphasis on overall trial results is that, when there is definite and consistent evidence of benefit (and negligible hazard) in all categories of patients that have been studied extensively (such as for statins in the prevention of major vascular events)⁸, then although the relative benefit in another (relatively unstudied) category might not be exactly the same, it is unlikely to be vastly different and, in particular, is extremely unlikely to be zero. Nonetheless, “exploratory” data-derived subgroup analyses are still widely reported in medical journals and at scientific meetings, with potential adverse consequences for medical care.

An example of how subgroup analyses have resulted in inappropriate management of patients is provided by the early trials of aspirin for the secondary prevention of stroke. Here, emphasis on the results in men led to a situation where, for almost 20 years, the US Food and Drug Administration approved the use of aspirin only for men; subsequent evidence shows this to have been a mistake, with aspirin reducing the risk of vascular events among high-risk people by about one quarter irrespective of sex.²⁴ A further example is provided by the large Italian GISSI-1 trial comparing streptokinase versus control after acute MI. The overall results favored streptokinase but subgroup analyses suggested that streptokinase was beneficial only in patients without prior MI. Fortunately, the GISSI investigators were circumspect about this finding³ and their caution turned out to have been wise, as a subsequent overview of all the large fibrinolytic trials showed that the proportional benefits were similar, irrespective of a history of MI.¹ Many thousands of patients with a previous history of MI might well have been denied fibrinolytic therapy, however, if the apparent pattern of the results in the GISSI-1 subgroups had been believed.

Avoidance of moderate random errors

Trials may produce false-negative results

Whereas the avoidance of moderate biases requires careful attention to both the randomization process and the analysis and interpretation of the available trial evidence, the avoidance of moderate random errors requires large studies. When making inferences about the likely true effect of a drug based on observations in a clinical trial, there are two types of error that can be made. A type I error occurs if a trial reaches a false-positive result, i.e. when it appears that a beneficial treatment effect has been demonstrated but the drug is actually ineffective. The second, type II, error occurs when a trial achieves a false-negative result, i.e. when the estimated effect of a beneficial treatment fails to reach statistical significance. A critical part of the design of any clinical study is a decision about how small these type I (α) and type II (β) error rates need to be. Together with an estimate of the minimum size of the effect one wishes to detect, these error rates determine the number of events required in a trial. The smaller the desired type I and type II error rates for a trial, the more patients that trial will need to recruit to be able to demonstrate any true treatment effects. Conversely, for a fixed sample size, the “power” (which is the a priori probability, 1 – β, of avoiding a false negative) of a trial to detect “meaningful” treatment effects reduces rapidly if the true magnitude of a treatment effect has been overestimated at the design stage. For example, as illustrated in Figure 3.1, in a trial of 10000 participants in which one-fifth of the control group has the primary endpoint, the power (at a type I error rate of 1%) to detect a true relative risk reduction of 20% would be excellent (> 99%), but the power to detect a true reduction of 10% would be less than 1 in 2.

Figure 3.1 Power to detect different relative risk reductions in a trial of 10 000 patients (5000 active vs 5000 control), an outcome rate of 20% in the control group and a type I error rate of 0.01.

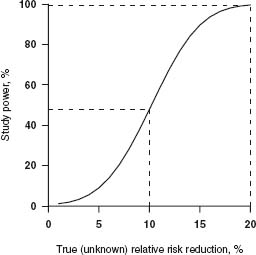
The power of a trial to identify a true treatment effect is greatly reduced if the true relative risk reduction is smaller than anticipated. However, it is also reduced if the study outcome occurs in a smaller than expected proportion of those randomized. Trials of major outcomes therefore need to accumulate large numbers of primary endpoints before the results can be guaranteed to be statistically (and hence medically) convincing. For example, the early trials of intravenous fibrinolytic therapy for acute myocardial infarction were individually too small to provide reliable evidence about any moderate effects of this treatment on mortality, although several did identify an increased risk of serious bleeding. As a result, fibrinolytic therapy was not used routinely until the GISSI-1³ and ISIS-2² “mega-trials” provided such definite evidence of benefit that treatment patterns changed rapidly²⁷ It is worth noting, however, that GISSI-1 and ISIS-2 each included more than 10 000 patients and 1000 deaths but had they only been one-tenth as large, the observed reduction in mortality would not have been conventionally significant and would therefore have had much less influence on medical practice.

When a clinical trial fails to demonstrate a statistically significant difference between two treatment groups, either there is not a true difference or, if there is, the trial was too small to detect it. In some circumstances, however, an appropriate objective may be the demonstration that two or more treatments are equally effective, in which case the statistical framework for the trial analysis is quite different from that required when the aim is to demonstrate treatment differences. The underlying model assumptions in such an “equivalence” study are essentially a reversal of those used in a conventional study design: the null hypothesis, rather than being one of no true difference between treatments, is that a small true difference Δ of size at least δ, say, exists between treatments (i.e. |Δ| ≥ δ where δ > 0) and the aim is to accumulate evidence against this hypothesis. Hence, if the null hypothesis is rejected, the implication is that |Δ| < δ, i.e. the effects of each treatment differ by no more than the small amount δ. Similarly, in a non-inferiority trial, where the object is to demonstrate that a new drug is at least as good as an existing one, the null hypothesis would be expressed as Δ < -δ (assuming that positive values of Δ are taken to mean that the new drug is better than the old one). Rejection of this hypothesis would imply that Δ > -δ; that is, the new drug has either similar or superior effects to the old one. Appropriate selection of the null hypothesis for a given clinical question plays a critical role not only in determining the sample size needed, but also in dictating how the results should be interpreted. Unfortunately, there are numerous examples of trials that were designed to test for a difference between two drugs, but were subsequently interpreted under a different null hypothesis.

Effect of non-compliance on study power

Even in a situation where a trial is designed to have sufficient statistical power to address its primary hypothesis, study power can quickly be eroded through higher than expected levels of non-compliance. This is because the sample size needed to achieve a given power is inversely proportional to the square of the difference, between treatment groups, in the proportions taking study treatment or a non-study equivalent. For example, suppose a trial of 10 000 patients was originally designed so that it had 80% power, at a type I error rate of 5%, to address its primary hypothesis, but that the sample size calculations assumed full compliance among all trial participants. Then suppose that during the trial 20% of those allocated active treatment stop taking it (“drop outs”) and 10% of those allocated control start taking the active treatment, or non-study equivalent, instead (“drop ins”). In these circumstances, the actual sample size that would have been needed to maintain study power is 20000 patients (since 10000/[1 – 0.2 – 0.1]²

Stay updated, free articles. Join our Telegram channel

Join