The novice in blood gas application must master Chapter 2 before addressing the content in this chapter. Indeed, Chapter 5 deals with the less frequent and more subtle technical nuances of blood gas classification and analysis and may lead to confusion if routine blood gas classification is not fully understood. This chapter is intended for use when the clinician is faced with some real or perceived inconsistency in the reported information. Thus, at some point during the assessment of blood gas data, the clinician should briefly pause and consider the plausibility, consistency, and harmony of the various recorded data. Assessment of the consistency of the reported measurements is recommended in comprehensive and systematic acid-base assessment by most experts.176 To ensure accuracy, blood gas values should be evaluated for internal consistency and external congruity. Assuming normal, constant metabolic status, the amount that pH will change in response to a given PaCO2 change is constant and is termed the acute PaCO2–pH relationship. The acute PaCO2–pH relationship for both increases or decreases in PaCO2 is shown in Table 5-1. A different pH change factor is necessary for a decrease in PaCO2 than for an increase in PaCO2 because of the logarithmic nature of these relationships. Table 5-1 Important landmarks in the relationship between PaCO2 and pH are shown in Table 5-2. It may be useful for the clinician to memorize these relationships. When a more precise calculation is desired, specific calculation of the expected pH for any PaCO2 can also be accomplished by application of the formulas shown in Box 5-1. Table 5-2 Important Landmarks of Acute PaCO2–pH Relationship The possible outcomes of indirect metabolic assessment based on comparison of actual and expected pH are defined in Table 5-3. When the actual pH is equal to the expected pH ±0.03, the metabolic status must be normal. When the actual pH is significantly more acidic than expected (i.e., more than 0.03 pH units lower), a metabolic acidosis must be present. Conversely, when actual pH is significantly more alkaline (more than 0.03 pH units) than expected, a metabolic alkalosis (nonrespiratory condition tending to cause alkalemia) must be present. These conclusions closely parallel metabolic diagnosis that is made directly with the [BE]ecf to be discussed later in this chapter. Table 5-3 A similar tool for detecting technical error may be referred to as the rule of eights, which provides a mechanism for predicting the plasma bicarbonate when the pH and PaCO2 are known. If the reported bicarbonate differs significantly from the bicarbonate calculated via the rule of eights (e.g., >4 mEq/L difference), a technical error is likely present. To calculate the predicted plasma bicarbonate, the PaCO2 is multiplied by a factor that varies with the pH. The factor to be used with a given pH can be found in Table 5-4. Table 5-4 Rule of Eights (Factor × PaCO2) = Predicted bicarbonate The Henderson equation to be described later in Chapter 8 can be modified to relate [H+] in nanequivalents per liter (instead of pH) to PaCO2 and [HCO3] as shown in Equation 5-1. Thus, if any two of these three variables are known the third variable can be calculated. There is a near-linear relationship between [H+] in nEq/L and pH over the pH range (7.20 to 7.50) shown in Table 5-5. It can also be seen that this linear relationship begins to deteriorate quickly beyond this range, especially with acidemia. Table 5-5 Relationship Between pH and [H+] By converting [H+] to pH, Equation 5-1 can be used to check internal consistency of questionable blood gases. This equation is especially useful because it can be used to determine any of the three variables (i.e., pH, PaCO2, or [HCO3]) if the other two variables are known. The acid-base map is discussed in detail in Chapter 14 (see Fig. 14-1), which addresses the identification of mixed acid-base disturbances. Using an acid-base map, one can easily plot two acid-base variables on the map and determine the third. When readily available, the acid-base map is probably the easiest and most expedient way to assess internal consistency. The plasma bicarbonate is also usually reported from the chemistry laboratory with standard electrolytes as total CO2 ([total CO2]). Because plasma [HCO3] comprises approximately 95% of total CO2, these two measurement may essentially be viewed as being interchangeable.176 177 One caveat is that total CO2is measured in the chemistry laboratory using venous blood, which is typically 2 to 3 mEq/L higher in bicarbonate. Nevertheless, total CO2 is, for all practical purposes, an index of plasma bicarbonate. Therefore, the electrolyte report may be used as a crosscheck regarding the accuracy of the [HCO3] reported on the blood gas report. As discussed in Chapter 8, CO2 is transported in the blood as bicarbonate, dissolved CO2, and carbamino-compounds. Bicarbonate and dissolved CO2 are responsible for almost all of the CO2 present in the blood plasma. Therefore, total CO2, usually reported in mEq/L, is presumed to be equal to the sum of CO2 dissolved in the plasma and plasma bicarbonate, which is shown in Equation 5-2. PaCO2 may be multiplied by the conversion factor (0.03 mEq/L/mm Hg) to determine the dissolved CO2 concentration in mEq/L. To calculate the specific [HCO3], dissolved CO2 in mEq/L is subtracted from the reported total CO2 (see Equation 5-3). The difference represents plasma bicarbonate in mEq/L. Because the concentration of dissolved CO2 in mEq/L is so small (typically 1 to 2 mEq/L) and bicarbonate represents 95% of the total CO2 value, gross inspection of the total CO2 provides a reliable estimation of plasma bicarbonate even without this calculation.
Accuracy Check and Metabolic Acid-Base Indices
ACCURACY CHECK
Internal Consistency
Techniques for Evaluating Internal Consistency
Acute PaCO2–pH Relationship
PaCO2 Change
pH Change
DECREASE
INCREASE
1 mm Hg
0.01
10 mm Hg
0.10
INCREASE
DECREASE
1 mm Hg
0.006
10 mm Hg
0.06
Expected pH
PaCO2
pH
20
7.60
25
7.55
30
7.50
35
7.45
40
7.40
50
7.34
60
7.28
70
7.22
80
7.16
90
7.10
Indirect Metabolic Status
Actual pH–Expected pH Relationship
Indirect Metabolic Status
Actual pH = expected pH ± 0.03
Normal metabolic status
Actual pH > expected pH + 0.03
Metabolic alkalosis
Actual pH < expected pH − 0.03
Metabolic acidosis
Rule of Eights
pH
Factor
7.60
8/8
7.50
6/8
7.40
5/8
7.30
4/8
7.20
2.5/8
7.10
2/8
Modified Henderson Equation
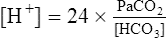 Equation 5-1
Equation 5-1
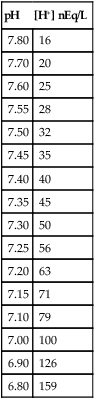
pH
[H+] nEq/L
7.80
16
7.70
20
7.60
25
7.55
28
7.50
32
7.45
35
7.40
40
7.35
45
7.30
50
7.25
56
7.20
63
7.15
71
7.10
79
7.00
100
6.90
126
6.80
159
Acid-Base Map
External Congruity
Laboratory to Laboratory Congruity
Total CO2
Total CO2 Components
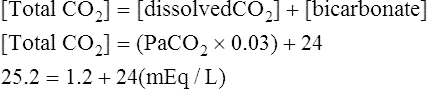 Equation 5-2
Equation 5-2
Bicarbonate Calculation from Total CO2
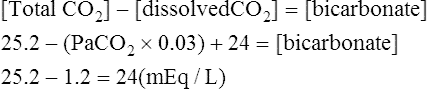 Equation 5-3
Equation 5-3![]()
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


Accuracy Check and Metabolic Acid-Base Indices
Only gold members can continue reading. Log In or Register to continue
