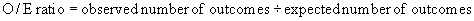NOMENCLATURE

During the 1990s, both the Society of Thoracic Surgeons (STS) and the European Association for Cardio-Thoracic Surgery (EACTS) created databases to assess the outcomes of congenital cardiac surgery.⁸ Beginning in 1998, these two organizations collaborated to create the International Congenital Heart Surgery Nomenclature and Database Project.⁶ By 2000, a common nomenclature, along with a common core minimal data set, were adopted by EACTS and STS and published in the Annals of Thoracic Surgery.⁶ Also in 2000, the Association for European Paediatric Cardiology published, in Cardiology in the Young, an international system of nomenclature for congenital cardiac disease named the European Paediatric Cardiac Code.^4,5,49,50

The developers of these two systems of nomenclature view these initiatives as complementary and not as competitive. Consequently, on Friday, October 6, 2000, the International Nomenclature Committee for Pediatric and Congenital Heart Disease was established.^49,50,55 In January, 2005, this International Nomenclature Committee was constituted in Canada as the International Society for Nomenclature of Paediatric and Congenital Heart Disease. The working component of this international nomenclature society has been the International Working Group for Mapping and Coding of Nomenclatures for Paediatric and Congenital Heart Disease, also known as the Nomenclature Working Group. By 2005, the Nomenclature Working Group cross-mapped the nomenclature of the International Congenital Heart Surgery Nomenclature and Database Project of EACTS and STS with the European Paediatric Cardiac Code of the Association for European Paediatric Cardiology, and thus created the International Paediatric and Congenital Cardiac Code (IPCCC), which is available for free download from the internet (www.IPCCC.NET).

DATABASE STANDARDS

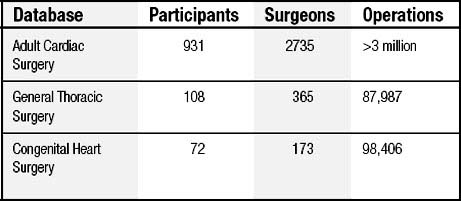
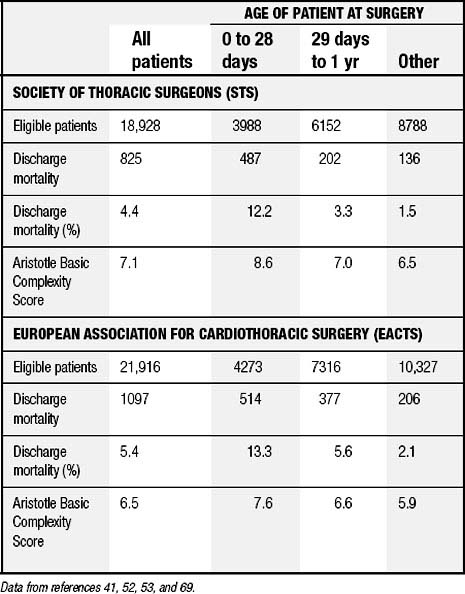
The IPCCC and the common minimum database data set created by the International Congenital Heart Surgery Nomenclature and Database Project are now used by both STS and EACTS.^58,63,69 From 1998 through 2007, this nomenclature and database were used by both of these organizations to analyze outcomes of over 150,000 patients undergoing surgical treatment for congenital cardiac disease.^76,82 Table 134-1 shows data culled from an analysis of over 40,000 patients undergoing surgery from 1998 through 2004.⁶⁹ Many publications generated from these two databases have reported outcomes after treatment for congenital cardiac disease in general, as well as outcomes for specific lesions.^58,63,69,85

Table 134–1 Aggregate Data from STS and EACTS for SurgeryPerformed between 1998 through 2004, Inclusive

The STS database is the largest clinical cardiothoracic surgical database in North America,⁸⁸ and it includes (as of August 8, 2008) 1111 participating sites with 3273 participating surgeons (Table 134-2).

Table 134–2 The Society of Thoracic Surgeons Database as of August 8, 2008

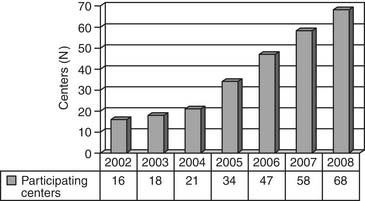
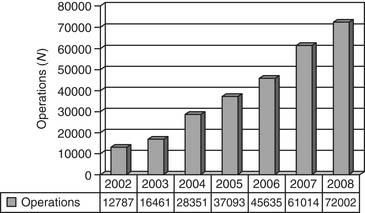
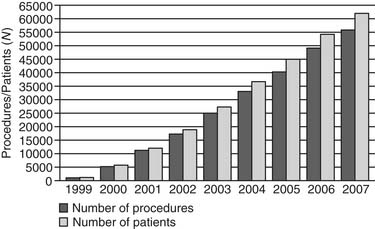
The Report of the 2005 STS Congenital Heart Surgery Practice and Manpower Survey, undertaken by the STS Workforce on Congenital Heart Surgery, documented that 122 centers in the United States and eight centers in Canada perform pediatric and congenital heart surgery.¹³⁰ As of June 2008, the STS Congenital Heart Surgery Database contains data from 68 of these 130 centers from North America, and it is now the largest database in North America dealing with congenital cardiac malformations. It has grown annually since its inception, in terms of both the number of participating centers submitting data and the number of operations analyzed (Figs. 134-1, 134-2, and 134-3). As of August 2008, the entire STS Congenital Heart Surgery Database contained data from 98,406 operations. The aggregate spring 2008 report from this database included data from the 4-year window of data harvest beginning January 1, 2004, and ending December 31, 2007, and included 72,002 operations submitted from 68 centers in North America (67 in the United States and one in Canada). One Japanese center also submits data, but these data are not included in the aggregate STS report.

Figure 134–1 Graph of the annual growth in the Society of Thoracic Surgeons (STS) Congenital Heart Surgery Database by number of participating centers submitting data. The aggregate spring 2008 report of this database includes data from 68 congenital heart surgery centers in the United States and Canada. (One Japanese center also submits data; however, these Japanese data are not included in the aggregate report produced by The Society of Thoracic Surgeons.)

(From Jacobs JP, Jacobs ML, Mavroudis C, Lacour-Gayet FG, Tchervenkov CI. Executive summary: the Society of Thoracic Surgeons Congenital Heart Surgery Database—Eighth Harvest [January 1, 2004–December 31, 2007]. The Society of Thoracic Surgeons and Duke Clinical Research Institute, Duke University Medical Center, Durham, NC, Spring 2008 Harvest.)

Figure 134–2 Graph of the annual growth in the Society of Thoracic Surgeons (STS) Congenital Heart Surgery Database by number of operations per averaged 4-year data collection cycle. The aggregate spring 2008 report from the database included data from the 4-year window of data harvest beginning January 1, 2004, and ending December 31, 2007, and included 72,002 operations submitted from 68 centers, 67 in the United States and one in Canada. (One Japanese center also submits data; however, these Japanese data are not included in the aggregate report produced by The Society of Thoracic Surgeons.)

(From Jacobs JP, Jacobs ML, Mavroudis C, Lacour-Gayet FG, Tchervenkov CI. Executive summary: the Society of Thoracic Surgeons Congenital Heart Surgery Database—Eighth Harvest [January 1, 2004–December 31, 2007]. The Society of Thoracic Surgeons and Duke Clinical Research Institute, Duke University Medical Center, Durham, NC, Spring 2008 Harvest.)

Figure 134–3 Graph of the annual growth in the Society of Thoracic Surgeons (STS) Congenital Heart Surgery Database by cumulative number of operations over time. (As of August 2008, the entire STS Congenital Heart Surgery Database contained data from 985, 406 operations.) The aggregate spring 2008 report from the database included data from the 4-year window of data harvest beginning January 1, 2004, and ending December 31, 2007, and included 72,002 operations submitted from 68 centers, 67 in the United States and one in Canada. (One Japanese center also submits data; however, these japanse data are not included in the aggregate report produced by The Society of Thoracic Surgeons.)

(From Jacobs JP, Jacobs ML, Mavroudis C, Lacour-Gayet FG, Tchervenkov CI. Executive summary: the Society of Thoracic Surgeons Congenital Heart Surgery Database—Eighth Harvest [January 1, 2004–December 31, 2007]. The Society of Thoracic Surgeons and Duke Clinical Research Institute, Duke University Medical Center, Durham, NC, Spring 2008 Harvest.)

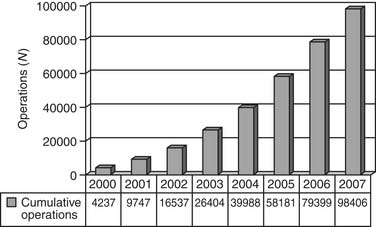
By January 1, 2008, the EACTS Congenital Heart Surgery Database contained 61,750 operations performed on 53,402 patients, including 12,109 operations on neonates, 20,487 on infants, 25,102 on children, and 4052 on adults (Fig. 134-4). The EACTS congenital registry continues to grow and has recently shown between 5000 and 10,000 new operations each year. This registry includes 274 units from 62 countries. Participants have access to over 300 on-line reports.

Figure 134–4 Graph of the annual growth in the European Association for Cardio-Thoracic Surgery Congenital Heart Surgery Database by both number of patients and number of operations.

(Graph courtesy of Bohdan Maruszewski of the Children’s Memorial Health Institute in Warsaw, Poland, director of the European Association for Cardio-Thoracic Surgery Congenital Heart Surgery Database, and president of the European Congenital Heart Surgeons Association.)

STRATIFICATION OF COMPLEXITY

The importance of the quantitation of complexity is that, in the field of pediatric cardiac surgery, analysis of outcomes using raw measurements of mortality, without adjustment for complexity, is inadequate. The mix of cases can vary greatly from program to program. Without stratification of complexity, the analysis of outcomes will be flawed. Two major multi-institutional efforts that have attempted to measure the complexity of congenital heart surgery are the Risk Adjustment for Congenital Heart Surgery-1 (RACHS-1) system,^∗ and the Aristotle Complexity Score^† The EACTS and STS congenital databases have included the Aristotle Complexity Score in their reports since 2002.^{41,52,53,59,72,78,86} In 2006, both databases also incorporated the RACHS-1 method into their reports.^72,78,86

To understand the RACHS-1 system and the Aristotle Complexity Score, one must first understand the following methods of adjusting for case mix¹⁰⁰: (1) stratification, (2) direct standardization, (3) regression analysis (i.e., risk modeling), and (4) indirect standardization. All four of these methods are considered forms of risk adjustment; however, only the third and fourth are considered risk modeling.

Stratification, also known as complexity stratification and risk stratification, is a method of adjusting for case mix in which patients are divided into relatively homogeneous groups called strata.¹⁰⁰ Comparisons of outcomes can then be made separately in each stratum. The goal is to ensure that comparisons are always performed on comparable patients. If patients in a stratum have a similar risk for adverse outcomes, then patients in the same stratum at different hospitals should be comparable. Although stratification is simple to explain and interpret, it does have limitations in its ability to adjust for case mix. First, the categorization of continuous variables is arbitrary. Second, stratification can adjust for only a small number of confounding variables. Finally, stratification controls only for differences in the variables that were used to create the strata. Other variables that are not used to create the strata may also have an impact on outcomes.

Direct standardization is a technique that can be used to compensate for the challenge of analyzing each stratum separately. With direct standardization, one calculates the stratum-adjusted standardized rate of mortality, combining multiple individual stratum-specific estimates into a single number. The adjusted standardized rate of mortality “is the rate of mortality that would be observed at a hospital if all of the hospital’s stratum-specific rates of mortality remained the same but the proportion of patients in each stratum was altered to reflect a ‘standard’ case-mix in some reference population.”¹⁰⁰ Direct standardization documents what the outcomes of each hospital would be if that hospital performed surgery on the entire population in the database while their stratum-specific rates of mortality remained the same.¹⁰⁰

Regression analysis, also known as regression modeling and risk modeling, is a method of adjusting for case mix in which a mathematical equation is developed that predicts an individual patient’s risk of experiencing an event, such as mortality, based on clinically relevant variables, such as age, weight, and cardiac diagnosis.¹⁰⁰ The choice of clinically relevant variables may be based on judgment or may be determined empirically from a large data set. Regression modeling is often used rather than stratification or direct standardization when the analysis necessitates adjustment for several confounder variables simultaneously.

Indirect standardization uses regression analysis and calculates “a predicted probability of the outcome for each patient within a hospital, summing these probabilities to determine the hospital’s expected number of outcomes, and finally comparing the observed number of outcomes to the expected number. The ratio of the observed to expected numbers of outcomes is often called the ‘observed-to-expected ratio,’ and is commonly termed the O/E ratio.”¹⁰⁰ The O/E ratio is calculated with the following formula:

If the observed-to-expected ratio for mortality is significantly greater than 1, this implies that that the rate of mortality is worse than would be expected given the case mix. If the observed-to-expected ratio for mortality is significantly less than 1, this implies that the rate of mortality is better than expected given the case mix.

Observed-to-expected ratios can be converted into standardized rates of mortality using the following formula:

Standardized rates of mortality document what the outcomes of each hospital would be if that hospital performed surgery on the entire population in the database while their performance remained the same.

Regression analysis is frequently used in fields such as adult cardiac surgery that have a large number of well-established risk factors, because the technique can adjust for multiple confounder variables simultaneously. The STS uses regression analysis to calculate O/E ratios, standardized rates of mortality, and other measures of performance for hospitals participating in their National Adult Cardiac Database.

Table 134-3 documents some fundamental differences and similarities in a comparison of risk adjustment with complexity stratification versus risk modeling with regression analysis. Complexity stratification, regression analysis, and risk modeling are all forms of risk adjustment; however, regression analysis is true risk modeling, whereas complexity stratification is not. Regression analysis requires making simplifying assumptions to determine the relationship between clinical factors and patient risk. Complexity stratification does not require these assumptions.¹⁰⁰ Most regression analyses produce only a single statistic summarizing a hospital’s overall outcome. Both stratification and regression analysis adjust only for risk factors that are explicitly included in the model. Observed differences in outcome might still be explained by factors that were either not measured or not included in the regression analysis or stratification scheme.¹⁰⁰

Table 134–3 Two Methods of Case-Mix Adjustment (or Risk Adjustment): Differences between Stratification and Regression Analysis

The STS Adult Cardiac Database uses true regression analysis risk modeling with indirect standardization. Unlike the STS Adult Cardiac Database, the STS and EACTS congenital databases rarely use true regression analysis risk modeling and instead use complexity stratification. In the STS Adult Cardiac Database, true risk modeling algorithms are based on more than 1.5 million patients undergoing coronary arterial bypass grafting (CABG) and over 100,000 patients undergoing isolated aortic valve replacement (AVR) or mitral valve replacement (MVR). As of August 2008, the STS Congenital Heart Surgery Database contained 98,406 operations involving more than 100 primary procedures, and it did have true risk modeling, although implementation of this methodology is a long-term goal. In the interim, the STS and EACTS congenital databases have used complexity adjustment to stratify outcome data.

The discrimination of tools for stratification of complexity as predictor of a given outcome such as mortality can be quantified by calculating the area under the receiver operating characteristic curve,¹³³ or C-statistic, as determined by univariable logistic regression. The C-statistic represents the probability that a randomly selected patient, who had the outcome of interest, such as mortality prior to hospital discharge, had a higher predicted risk for the outcome compared with a randomly selected patient who did not experience the outcome. The C-statistic is generally 0.5 to 1.0, with 0.5 representing no discrimination, that is a coin flip, and 1.0 representing perfect discrimination. For example, the model for risk adjustment of the STS Adult Cardiac Surgery Database for predicting 30-day mortality after surgery to place coronary arterial bypass grafts contains 28 clinical variables and has a C-statistic of 0.78.^133,134

Until recently, large multi-institutional databases for congenital and pediatric cardiac surgery have not been available, so regression analysis risk modeling with indirect standardization had not been developed for the multi-institutional database for congenital and pediatric cardiac surgery. Instead, databases tracking outcomes of congenital and pediatric cardiac surgery have used complexity stratification based more on expert opinion (or subjective probability) than on objective data, which have been lacking. In the field of congenital and pediatric cardiac surgery, efforts have been made to measure the complexity of pediatric cardiac operations using the RACHS-1 method and the Aristotle Complexity Score, as mentioned previously. Both systems were derived in large part from subjective probability, or expert opinion. Both systems are currently in wide use throughout the world and have been shown to correlate reasonably well with outcome. Efforts are underway to develop the next generation of these systems, which will be based more on objective data but will continue to use subjective probability when objective data are lacking. A goal is to reevaluate and further refine these tools so that they can be, to a greater extent, derived from empirical data. During this process, ideally, the mortality elements of both the methods will eventually unify and become one and the same.

Risk Adjustment for Congenital Heart Surgery-1

The RACHS-1 method^{46,54,131,135–137} was developed by a group of investigators under the leadership of Dr. Kathy Jenkins at Children’s Hospital Boston.⁴⁶ The goal was to adjust for baseline differences in case mix and risk when comparing mortality prior to discharge from the hospital among groups of patients less than 18 years of age undergoing surgery for congenital cardiac disease. A nationally representative 11-member panel of pediatric cardiologists and cardiac surgeons used clinical judgment to place 207 surgical procedures defined by the codes from the Current Procedural Terminology 4 and the International Classification of Diseases, Ninth Revision, Clinical Modification (ICD-9-CM) into six groups judged to have similar risks for in-hospital mortality. These risk categories were then refined using empirical data of mortality prior to discharge from the hospital, from the Pediatric Cardiac Care Consortium and three state-wide hospital discharge databases (Illinois from 1994 and Massachusetts and California from 1995). The final method included six risk categories, with category 1 representing the lowest risk and category 6 the highest, as well as three additional clinical factors: (1) age at operation, with three categories—30 days or less, 31 days to 1 year, and 1 year or more, (2) prematurity, and (3) the presence of a major noncardiac structural anomaly such as a tracheoesophageal fistula.

Although the use of administrative data coded with the ICD-9-CM has sometimes been identified as a potential shortcoming, the developers of the RACHS-1 method point out that these administrative data have, up to now, been used to support a significant fraction of research about health-care services pertinent to pediatric cardiology. Furthermore, algorithms that use these administrative data to examine outcomes of surgery for congenital cardiac diseases have been endorsed by the U.S. Agency for Healthcare Research and Quality.⁵⁴ It is recognized that administrative data coded with the ICD-9-CM are frequently the only available data that are population based and thus can be a crucial source of information for certain types of research. The RACHS-1 method has shown excellent performance in a variety of settings and has been used extensively in research on clinical outcomes in the United States and abroad.^131,136,137

Using several databases, this methodology has been evaluated with respect to the correlation between the level from the RACHS-1 tool and observed discharge mortality. In the administrative hospital discharge database used in the development of the RACHS-1 method, the C-statistic was 0.749 for risk category alone, and 0.814 when additional clinical factors were incorporated. In the clinical database of the Pediatric Cardiac Care Consortium, the C-statistic was 0.784 for risk category alone, and 0.811 with the additional factors.⁴⁶ Subsequent work in a variety of databases has resulted in C-statistics for the RACHS-1 method ranging from 0.74 to 0.85.

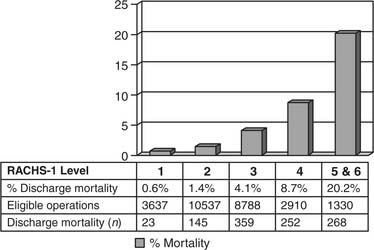
The EACTS and STS congenital databases have included the RACHS-1 system in their database reports since 2006. In the 2006 report of the STS Congenital Heart Surgery Database,⁷⁸ 85.8% of eligible cardiac index operations, or 27,202 out of 31,719 operations, were eligible for analysis by the RACHS-1 system (Fig. 134-5).

Figure 134–5 Graph of discharge mortality by complexity level using the Risk Adjustment for Congenital Heart Surgery-1 (RACHS-1) system. The data are from the Society of Thoracic Surgeons (STS) 2006 Congenital Heart Surgery Database of 45,635 cases during the 4 years of 2002 through 2005, inclusive.

(Adapted from Jacobs JP, Jacobs ML, Lacour-Gayet FG,et al. Stratification of complexity improves utility and accuracy of outcomes analysis in a multi-institutional congenital heart surgery database – application of the RACHS-1 and Aristotle Systems in the STS Congenital Heart Surgery Database. Pediatr Cardiol, in press.)

The Aristotle Complexity Score

In 1999, under the leadership of Dr. Francois Lacour-Gayet, the Aristotle Committee was created to address the issue of stratification of complexity in surgery for congenital cardiac diseases. The developers of this tool recognized that standard methods of benchmarking in quality of care assessment were based on stratification of risk, with nearly exclusive emphasis on the measurement of the outcome of operative mortality. They believed that to assess outcomes, including comparison of outcomes between centers, and to establish a platform for continuous improvement in quality, stratification based on the risk for mortality alone is insufficient. The fundamental principle of the Aristotle Complexity Score^{56,57,63,80,84,138–141} is to define complexity as a constant for the challenge presented by a given surgical procedure.⁵⁶ The Aristotle committee postulated that the complexity of a given procedure in surgery for congenital cardiac diseases is the sum of three factors or indices: (1) the potential for operative mortality, (2) the potential for operative morbidity, and (3) the technical difficulty of the operation.

Lacour-Gayet and the Aristotle Committee created a tool for stratification of complexity and called it the Aristotle Complexity Score, following Aristotle’s belief in the importance of current opinion. In the year 350 BCE, in Rhetoric, Book 1, Aristotle stated, “When there is no scientific answer available, the opinion (Doxa) perceived and admitted by the majority has the value of truth.”

Lacour-Gayet and the Aristotle Committee have differentiated the concepts of complexity and risk and have stated, “Complexity is a constant precise value for a given patient at a given point in time; performance varies between centers and surgeons. In other words, in the same exact patient with the same exact pathology, complexity is a constant precise value for that given patient at a given point in time. The risk for that patient will vary between centers and surgeons because performance varies between centers and surgeons.”⁶³

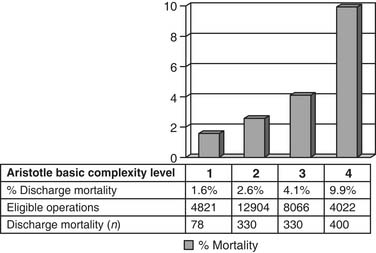
Under the leadership of Lacour-Gayet and the Aristotle Committee, the Aristotle Basic Complexity Score was developed by a panel of experts, made up of 50 surgeons who repair congenital cardiac defects in 23 countries and represent several major professional societies. The Aristotle Basic Complexity Score allocates a basic score to each operation, varying from 1.5 to 15, with 15 being the most complex, based on the primary procedure of a given operation as selected from the Procedure Short List of the version of the IPPCCC derived from the International Congenital Heart Surgery Nomenclature and Database Project of the STS and EACTS. The Aristotle Basic Complexity Score represents the sum or aggregate of scores assigned to a given procedure for the three components of complexity—potential for mortality, potential for morbidity, and technical difficulty—each of which varies from 0.5 to 5. To facilitate analysis across large populations of patients, each procedure is then assigned an Aristotle Basic Complexity Level, which is an integer ranging from 1 to 4 based on the Aristotle Basic Complexity Score (Table 134-4).

Table 134–4 Correlation between Aristotle Basic Complexity Levels and Scores

Aristotle Basic Complexity Level	Aristotle Basic Complexity Score	Procedures∗ (N)
1	1.5 to 5.9	29
2	6.0 to 7.9	46
3	8.0 to 9.9	45
4	10.0 to 15.0	25

∗ Of 145 procedures from the original Procedure Short List of the International Nomenclature used by the Society of Thoracic Surgeons and the European Association for Cardio-Thoracic Surgery.

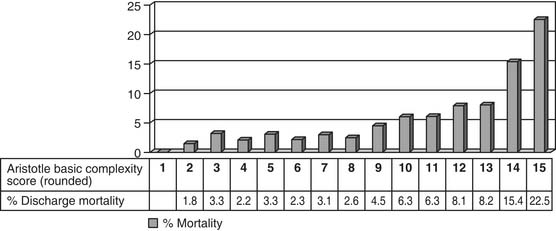
Both the score and the level are useful tools, and the appropriate tool can be chosen to match the required analysis.^57,63 Initial data from the STS and EACTS multi-institutional databases indicate that the Aristotle Basic Complexity Score and Aristotle Basic Complexity Level correlate well with mortality prior to discharge from the hospital after surgery for congenital cardiac diseases.^63,80,84

In an analysis of data from the STS and EACTS congenital databases, the Aristotle Basic Complexity Score is associated with (1) mortality, with a C-statistic of 0.70, and (2) prolonged postoperative length of hospital stay, defined as postoperative length of stay greater than 21 days, with a C-statistic of 0.67.⁸⁴ This implies that the Aristotle Basic Complexity Score generally discriminates between low-risk and high-risk operations.⁸⁴ In this study,⁸⁴ prolonged postoperative length of hospital stay was regarded as a very general proxy measure of morbidity. Additional concomitant procedures may alter the complexity of an operation. Discrimination was slightly greater when the analysis was restricted to operations consisting of a single procedure, and excluded operations with multiple-component procedures, with a C-statistic of 0.73 for mortality and a C-statistic of 0.70 for prolonged postoperative length of hospital stay. When the mortality and morbidity components of the Aristotle Basic Complexity Score were examined separately, the mortality component predicted mortality with a C-statistic of 0.68, and the morbidity component predicted prolonged postoperative length of hospital stay with a C-statistic of 0.67. Finally, when fixed, hospital-specific intercepts were added to the logistic regression models along with the Aristotle Basic Complexity Score, the C-statistic was 0.74 for mortality and 0.72 for prolonged postoperative length of hospital stay. For comparison, the C-statistics of the models containing hospital effects only, excluding Aristotle Basic Complexity Score, were 0.63 for mortality and 0.62 for prolonged postoperative length of hospital stay. Thus, adding the Aristotle Basic Complexity Score to a model containing hospital effects appears to improve its discrimination.⁸⁴

The STS and EACTS congenital databases have included the Aristotle Basic Complexity Score and Aristotle Basic Complexity Level in their database reports since 2002. In the 2006 report of the STS Congenital Heart Surgery Database,⁷⁸ 94.0% of eligible cardiac index operations, or 29,813 out of 31,719 operations, were eligible for analysis by the Aristotle Basic Complexity Score and Level (Figs. 134-6 and 134-7).

Figure 134–6 Graph of discharge mortality by complexity level using the Aristotle Basic Complexity Level. The data are from the Society of Thoracic Surgeons (STS) 2006 Congenital Heart Surgery Database of 45,635 cases during the 4 years of 2002 through 2005, inclusive.

(Adapted from Jacobs JP, Jacobs ML, Lacour-Gayet FG, et al. Stratification of complexity improves utility and accuracy of outcomes analysis in a multi-institutional congenital heart surgery database–application of the RACHS-1 and Aristotle Systems in the STS Congenital Heart Surgery Database. Pediatr Cardiol, in press).

Figure 134–7 Graph of the relationship between discharge mortality and the rounded Aristotle Basic Complexity (ABC) Score. One has the opportunity to stratify operations further into additional complexity groupings when the scope of the analysis is expanded beyond ABC Level to incorporate ABC Score.

The Aristotle Comprehensive Complexity Score adds further discrimination to the Basic Score by incorporating two sorts of patient-specific complexity modifiers: (1) procedure-dependent factors, including anatomic factors, associated procedures, and age at procedure, and (2) procedure-independent factors, including general factors such as weight and prematurity, clinical factors such as preoperative sepsis or renal failure, extracardiac factors such as duodenal atresia and imperforate anus, and surgical factors such as reoperative sternotomy. Additional points, up to a maximum of 10, are added to the Basic Score to account for the added complexity and challenge imputed by these modifying factors. The Aristotle Comprehensive Complexity Score has been used by numerous investigators to analyze the outcomes from complex procedures.^138–141