The Ventricular Action Potential

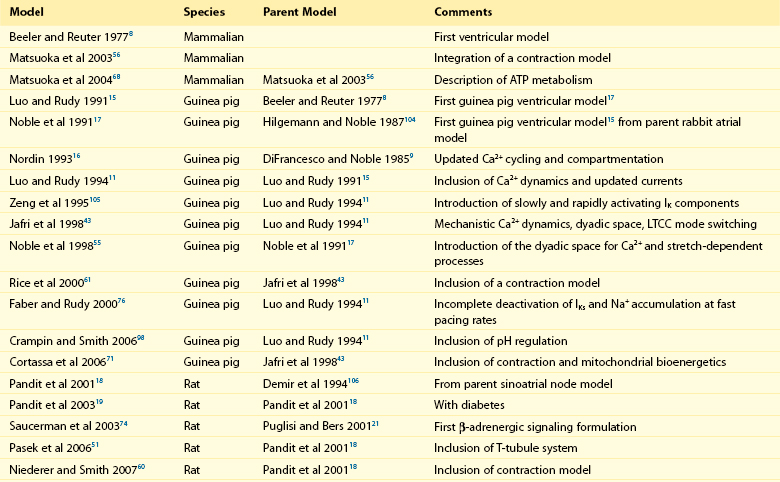
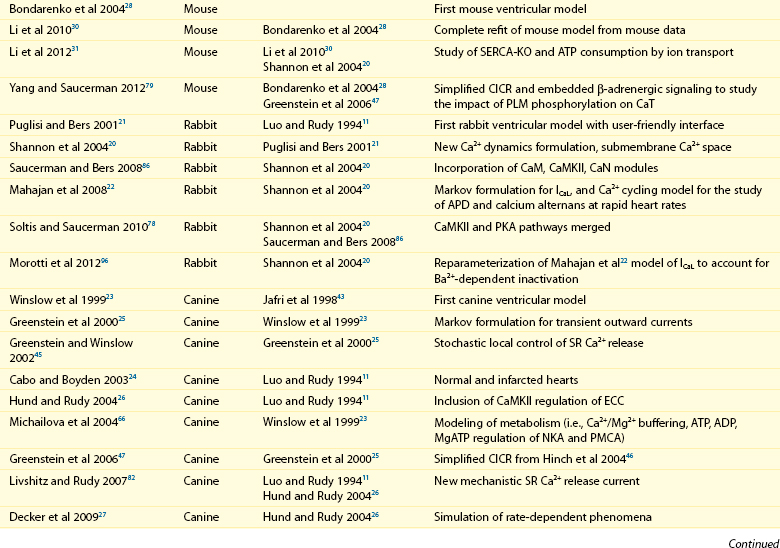
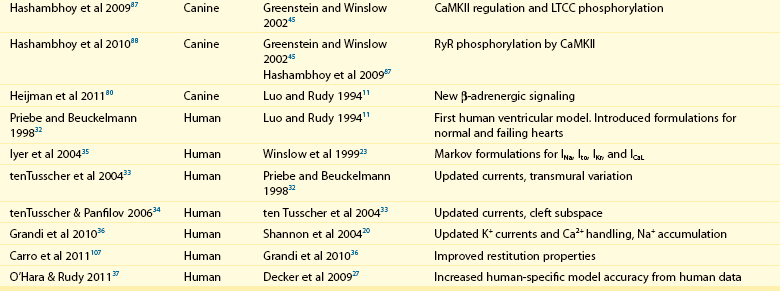
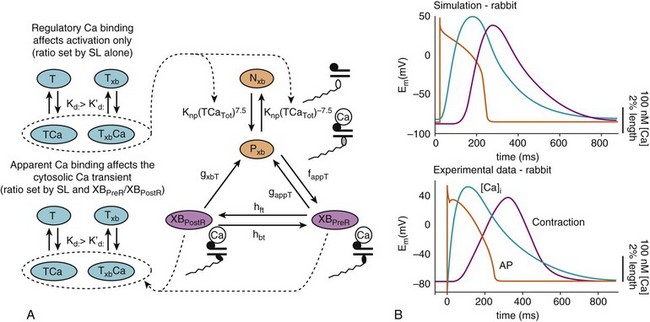
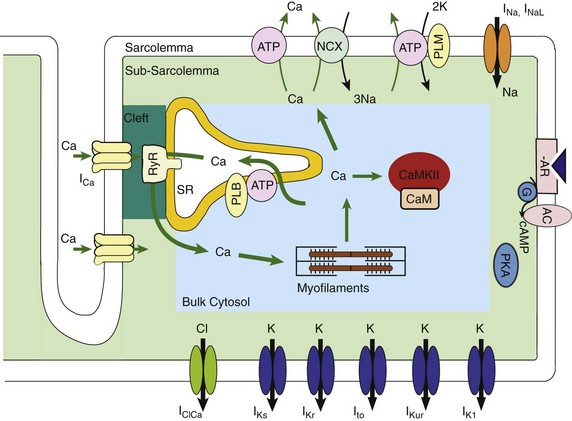
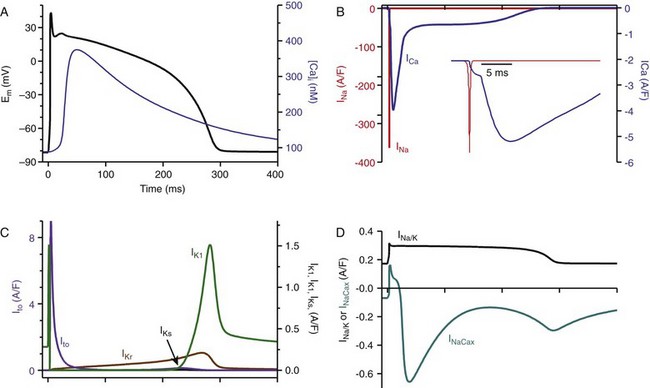
The action potential (AP) is a transient depolarization of the cell membrane that emerges from the dynamic behavior of a diverse population of membrane ion channels (depicted in Figure 32-1). A prototypical ventricular myocyte AP is shown in Figure 32-2, A (black). The AP exhibits a steep upstroke, followed by a sustained slowly decaying plateau phase, which eventually gives way to repolarization. Below the AP are shown the associated depolarizing currents, which are carried by inward Na⁺ and Ca²⁺ currents. Under physiological conditions, the Na⁺ current (I_Na) activates rapidly, producing the AP upstroke, and then inactivates completely (Figure 32-2, B, red). The L-type Ca²⁺ current (I_CaL) inactivates more slowly (Figure 32-2, B, blue), and less completely, allowing for the inward Ca²⁺ current to maintain the plateau phase of the AP. The influx of Ca²⁺ via I_CaL triggers the release of Ca²⁺ from the sarcoplasmic reticulum (SR), the subcellular organelle that stores and releases the majority of Ca²⁺ during each heartbeat.¹ This event is known as Ca²⁺-induced Ca²⁺ release (CICR) and will be discussed in Section II. The SR then actively re-sequesters Ca²⁺ via the SR Ca²⁺ adenosine triphosphatase (ATPase) (SERCA), which is the primary mechanism removing Ca²⁺ from the cytosol to allow relaxation in between heartbeats.² Throughout this process, Ca²⁺ is buffered by Ca²⁺-binding proteins such as calmodulin (CaM) and troponin. The rise in cytosolic Ca²⁺ (Figure 32-2, A, blue) ultimately leads to cell contraction (see Section III). The intracellular Ca²⁺ signal also feeds back on the L-type Ca²⁺ channel (LTCC), mediating inactivation of the current, and therefore plays a role in influencing the AP shape. Furthermore, intracellular Ca²⁺ regulates a variety of processes including mitochondrial adenosine triphosphate (ATP) production (see Section IV), intracellular signaling (presented in Section V), and gene expression.

Various types of K⁺ channels (Figure 32-2, C) drive cell membrane repolarization. The transient outward currents (I_to and I_ClCa), carried by K⁺ and Cl⁻ respectively, determine the notch that follows the upstroke, and components of the delayed rectifier K⁺ current (I_Kr and I_Ks) contribute to AP repolarization. The inward rectifier current (I_K1) maintains and stabilizes the resting potential. Other important players in shaping properties of the cardiac AP are the Na⁺/K⁺ pump (NKA), which generates an outward current by extruding 3 Na⁺ ions and importing 2 K⁺ ions on each cycle, and the Na⁺/Ca²⁺ exchanger (NCX), which mostly operates in the Ca²⁺-extrusion mode and yields a net inward charge movement when 1 Ca²⁺ ion is exchanged for 3 Na⁺ ions (Figure 32-2, D). The plasma membrane Ca²⁺ ATPase (PMCA) also extrudes Ca²⁺ from the cell and finely regulates cytosolic Ca²⁺ levels.

Computational models of cardiac electrophysiology and the close interplay between model development and experimentation enabled us to achieve a quantitative understanding of the integrative behavior of the cardiac myocyte in health and disease (see Section VI). We will present the evolution of computational electrophysiological models from the early formulations to the most recent comprehensive descriptions integrating Ca²⁺ and other signaling pathways, force, and metabolism.

Early Canonical Models of the Cardiac AP

Hodgkin and Huxley laid the foundation for the use of integrative models in biology describing both voltage clamp measurements of membrane currents and an integrative AP model of the squid giant axon.3,4 Their modeling approach, which postulated that gating mechanisms regulated membrane permeability, whereby distinct entities (i.e., gates) controlled the flux of both Na⁺ and K⁺ ions, has served to this day as a paradigm for a quantitative description of cell membrane excitability. In the early 1960s, Denis Noble presented the first computational models of a cardiac myocyte^5,6 and addressed the issue of whether Na⁺ and K⁺ current descriptions similar to those of Hodgkin and Huxley could be employed to account for the long AP plateau in Purkinje fibers. Modifications to Na⁺ and K⁺ current kinetics were able to generate a plateau, which was supported by the inward Na⁺ current. It is now known that Ca²⁺ currents, which had not yet been discovered and were later introduced in the McAllister-Noble-Tsien model,⁷ mainly support the AP plateau. Beeler and Reuter extended the latter model to develop the first computational ventricular myocyte model.⁸ Their work introduced a time-varying intracellular Ca²⁺ concentration and reinforced the idea that a balance between K⁺ and Ca²⁺ currents maintains the AP plateau, and repolarization is regulated by activation of K⁺ and inactivation of Ca²⁺ currents. Aspects of intracellular Ca²⁺ handling were introduced in the DiFrancesco-Noble Purkinje cell,⁹ which constituted the basis of all subsequent models of the cardiac myocyte. One of the landmarks in the development of models of ventricular electrophysiology was the formulation of the dynamic Luo-Rudy ventricular cell model.^10,11 Important features of this model were the inclusion of the intracellular SR compartment, time-varying intracellular ion concentrations, and ion pumps and exchangers. The continued interactive iteration between experiments and simulations has led to improved mechanistic insights into cardiac myocyte electrophysiology, as was recently reviewed.¹² Table 32-1 summarizes the existing models of the ventricular myocyte, based on previous classifications.^12–14

Species-Specific and Human Models

Although most of the early models generically integrated experimental data from mammalian hearts (mostly guinea pig11,15–17), by the mid-1990s, electrophysiological studies had shown species differences in AP waveforms and ionic currents (e.g., mouse and rat APs lack a plateau phase), but exhibited rapid repolarization and very short AP duration (APD) if compared with the prominent plateau phase and long AP seen in humans, rabbit, guinea pig, and dog. Thus, the emphasis shifted to more detailed models on the basis of data obtained from isolated cells from one particular species (see Table 32-1). Rat ventricular cell models have been developed,^18,19 as well as rabbit^20–22 and dog.^23–27 Mouse models^28–31 are becoming increasingly important, as genetic manipulation in mice has proven to be a powerful tool for studying the physiological effects of gene mutations, knockouts, and overexpression. The wealth of experimental data that can be measured in these mouse models cannot be obtained in humans, but integrative models provide a systematic framework to make inferences concerning the effects expected in other species and in the clinical setting (see caveat later).

The first human ventricular cell model was published by Priebe and Beuckelmann³² and was largely based on the dynamic Luo-Rudy model,¹¹ in which formulations for the major ionic currents were adjusted to the data (limited at that time) available for human ventricular cells. The tenTusscher et al³³ model and an updated version³⁴ included many reformulated currents and recapitulated several electrophysiological phenomena. The Iyer et al³⁵ model addressed whole-cell Ca²⁺ homeostasis carefully. The most relevant ionic currents were based almost entirely on data from human channels expressed in non-myocytes and formulated with Markovian chains, which made this model much more complex than those previously described. The Grandi-Pasqualini-Bers model³⁶ included K⁺ current reformulations using undiseased human data, provided an accurate description of Ca²⁺ and Na⁺ handling in the human ventricular myocyte, and accurately reproduced diverse aspects of excitation-contraction coupling (ECC), including the contribution of various K⁺ currents to repolarization reserve, the phenomenon of reverse-rate dependence of APD upon K⁺ current block, and feedback on the effects of changes in Na⁺ levels on APD and Ca²⁺ handling. The O’Hara and Rudy model³⁷ included new measurements for I_CaL, K⁺, and NCX currents from undiseased human ventricle, and included the effects of Ca²⁺/CaM-dependent protein kinase II (CaMKII) on ionic currents and Ca²⁺ cycling. This model also reproduced early afterdepolarizations (EADs) and alternans.

Species-specific models provide a useful platform for investigating species differences (e.g., with respect to arrhythmia and drug response). Comparison of AP repolarization, rate-dependent behavior, and drug response in human, dog, and guinea pig demonstrated major species differences and suggested that great caution should be taken when attempts are made to extrapolate results from nonhuman species to human cellular electrophysiology.³⁸