Measurement of Ventricular Volumes, Ejection Fraction, Mass, Wall Stress, and Regional Wall Motion
Michael A. Fifer
William Grossman
Cardiac angiography was introduced initially to provide qualitative information regarding anatomic abnormalities of the cardiovascular system. Subsequently, it became apparent that quantitative information derived from cineangiography could provide insight into functional abnormalities of the heart as well. Direct measurement of ventricular dimension, area, and wall thickness allows calculation of volume, ejection fraction, mass, and wall stress. Assessment of pressure-volume relationships provides additional information regarding systolic and diastolic function of the ventricular chambers. Finally, the techniques developed to assess regional left ventricular wall motion have proved useful in the evaluation of patients with coronary artery disease. Therefore, the ventricular angiograms obtained by the techniques described in Chapter 17 can be used to derive quantitative descriptors of geometry and function.
VOLUMES
Technical Considerations
As discussed in detail in Chapter 17, ventriculograms are generally recorded in digital format at 15 to 30 frames per second (fps), and radiographic contrast material is usually injected into the left ventricle at rates of 7 to 15 mL/second for a total volume of 25 to 45 mL. Alternatively, the left ventricle may be visualized from contrast injections into the pulmonary artery, the left atrium (by the trans-septal technique), or, in cases of severe aortic insufficiency, the aortic root. Attention to catheter position and injection rate minimizes the occurrence of ventricular ectopy during contrast studies; this is important because analysis of extrasystoles and postextra-systolic beats cannot be used for proper assessment of basal ventricular function.
With the widespread availability of computer systems, the technique of determining ventricular volumes has evolved from a handheld planimeter with pencil and paper (or a calculator) to semiautomated software packages. The principles important in accurate determination of volume, however, apply equally to manual and computer-based techniques. For example, the need for magnification correction applies to both manual and automated techniques of volume determination.
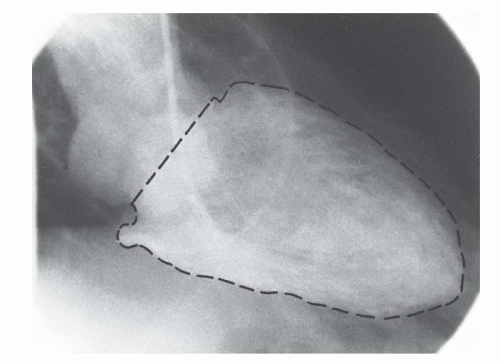
In the first step in assessing left ventricular chamber volume, the left ventricular outline or silhouette is traced. The ventricular silhouette should be traced at the outermost margin of visible radiographic contrast so as to include trabeculations and papillary muscles within the perimeter (Figure 21.1). The aortic valve border is defined as a line connecting the inferior aspects of the sinuses of Valsalva. Some computer-based systems require that the entire ventricular silhouette be traced manually; others incorporate a semiautomated edge-detection algorithm wherein some points on the ventricular silhouette are entered manually and others are supplied by the computer software.
To facilitate the calculation of left ventricular volume, the ventricle is often approximated by an ellipsoid.1, 2, 3 Alternatively, techniques based on Simpson’s rule, which is independent of assumptions regarding ventricular shape, may be used.4 According to this rule, the volume of any object is
equal to the sum of the volumes of individual slices of known thickness composing the object. Thinner slices will result in more accurate measurements.4 Contemporary software programs may allow the user to choose between these two techniques. Because the x-rays emanate from a point source, they are nonparallel; correction must therefore be made for magni fication of the ventricular image onto the detector. Finally, ventricular volumes calculated by most mathematical techniques overestimate true ventricular chamber volume, so that regression equations must be used to correct for the overestimation.
equal to the sum of the volumes of individual slices of known thickness composing the object. Thinner slices will result in more accurate measurements.4 Contemporary software programs may allow the user to choose between these two techniques. Because the x-rays emanate from a point source, they are nonparallel; correction must therefore be made for magni fication of the ventricular image onto the detector. Finally, ventricular volumes calculated by most mathematical techniques overestimate true ventricular chamber volume, so that regression equations must be used to correct for the overestimation.
Biplane Formula
Biplane left ventriculography may be performed in the anteroposterior (AP) and lateral projections,2 the 30° right anterior oblique (RAO) and 60° left anterior oblique (LAO) projections,5 or angulated projections (e.g., 45° RAO and 60° LAO-25° cranial).6 Although it has a complex geometric shape, the left ventricle can be approximated with considerable accuracy by an ellipsoid2 (Figure 21.2). The volume of an ellipsoid is given by the equation
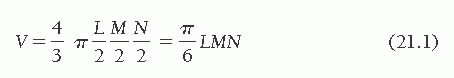
where V is volume, L is the long axis, and M and N are the short axes of the ellipsoid. The long axis, L, is taken practically to be Lmax, the longest chord that can be drawn within the ventricular silhouette in either projection. To determine M and N, each of the biplane projections of the left ventricle is approximated by an ellipse. M and N are taken to be the minor axes of these ellipses. They are calculated by the area–length method, as introduced by Dodge et al.2 from the silhouette areas and long-axis lengths in each projection, using the standard geometric formula for the area of an ellipse as a function of its major and minor axes. For biplane oblique
(RAO/LAO) left ventriculography, for example, the areas of the two ventricular silhouettes are given as
(RAO/LAO) left ventriculography, for example, the areas of the two ventricular silhouettes are given as
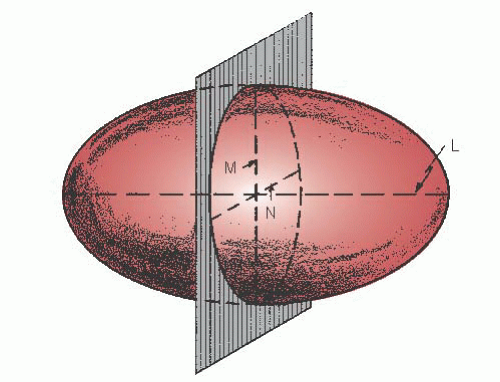 Figure 21.2 Ellipsoid used as a reference figure for the left ventricle. The long axis, L, and the short axes, M and N, are shown. |
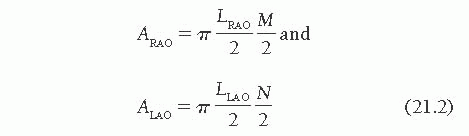
LRAO and LLAO are the longest chords that can be drawn in the RAO and LAO silhouettes, respectively. The area of each traced silhouette (Figure 21.1) is obtained by planimetry, and M and N are calculated by rearrangement as follows:
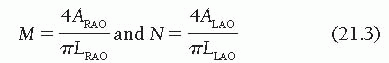
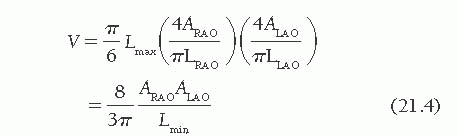
where Lmin is the shorter of LRAO and LLAO. Because LRAO is almost always longer than LLAO, LLAO is usually substituted for Lmin.
Equation (21.4) is derived for projections at right angles, or orthogonal projections, and is applicable to biplane oblique ventriculography in the 30° RAO and 60° LAO views, as just described, or for the older AP and lateral format. Although it is not valid theoretically for non-orthogonal projections (e.g., RAO and angulated LAO), it has been demonstrated empirically to be useful in those situations as well.6
Right ventricular volumes have been calculated from biplane AP and lateral images using a modification of the Dodge area-length technique7,8 or Simpson’s rule.8, 9, 10 Because right ventricular volumes are rarely calculated from cinean-giographic studies today, the reader is referred elsewhere for methodologic details.7, 8, 9, 10
Single-Plane Formula
The area-length ellipsoid method for estimating left ventricular chamber volume has been modified for use in the usual situation in which only single-plane measurements obtained in the AP or RAO projection are available.3,11, 12, 13 Inherent in single-plane methods is the assumption that the left ventricular shape may be approximated by a prolate spheroid—that is, an ellipsoid in which the two minor axes are equal.12 It is assumed that the minor axis of the ventricle in the projection used is equal to the minor axis in the orthogonal plane, which was not imaged. Recalling Eq. (21.1) for the general case of an ellipsoid:

If only single-plane (e.g., RAO) ventriculography is done, we assume that M = N and that L in the plane presented is the true long axis of the ellipsoid. M is calculated from the single-plane silhouette area (A) and L by the area-length method as M = 4A/pL. Therefore, the single-plane volume calculation becomes
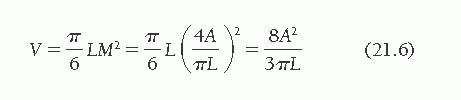
Magnification Correction: Single Plane
Correction may be accomplished by imaging a calibrated grid at the estimated level of the ventricle11 and submitting the grid to the same magnification process as that to which the ventricle is subjected. Use of x-ray systems in which the center of the ventricle can be positioned at a fixed point (iso-center), around which the x-ray tubes and image intensifiers rotate, allows for magnification correction without the use of grids.
The use of grids and other means of calculating magnification correction factors has been reassessed by Sheehan and Mitten-Lewis.14 They found that the error introduced by considering a large central square area of the grid rather than the portion encompassing a particular ventricular silhouette was negligibly small. Replacement of the grid by a circular disk did not significantly alter the calculated correction factor. Alternatively, the use of catheters with radiopaque markers separated by 1 cm also yielded accurate correction factors.
An approximation of the magnification correction may be obtained by considering the diameter of the catheter used for left ventriculography. However, there is a large potential percentage error in measurement of this small dimension, and the percentage error in volumes derived from it is roughly triple that in the linear correction factor. On the other hand, the error introduced into calculation of ejection fraction by this technique is much smaller than that in the calculation of ventricular volume; if it were not for the need for regression formulas (see later discussion), ejection fraction could be determined without regard to magnification.
In the single-plane formula, the cube of the linear correction factor adjusts the volume for magnification:
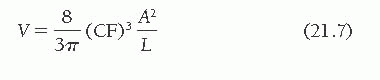
Magnification Correction: Biplane
In biplane studies, a correction factor (CF) must be calculated separately for each projection, yielding, in the case of biplane oblique cineangiography, CFRAO and CFLAO. The linear correction factor is multiplied by the measured lengths, and the square of this correction factor is multiplied by planimetered areas to convert to true
lengths and areas. Accordingly, the corrected volume of the ventricle is
lengths and areas. Accordingly, the corrected volume of the ventricle is
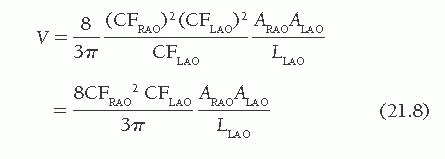
Regression Equations
Postmortem studies of hearts injected with contrast material have demonstrated that angiographic volumes calculated by Eq. (21.8) overestimate true left ventricular cavity volumes.2,4,5 This overestimation results in large part from the papillary muscles and trabeculae carneae, which do not contribute to blood volume but are nevertheless included within the traced left ventricular silhouette. Regression equations derived from these studies are used to adjust the calculated volumes. A list of the most commonly used regression equations is given in Table 21.1. For cine studies in the 60° RAO/30° LAO projections, Wynne et al.5 used postmortem casts, as shown in Figure 21.3, to derive the regression equation shown in Table 21.1.
Single-plane techniques tend to overestimate volume significantly, as compared with biplane methods, and this is reflected in the single-plane regression equations (Table 21.1). Regression equations are incorporated into commercial catheterization laboratory packages.
EJECTION FRACTION AND REGURGITANT FRACTION
Visual inspection of the cine images allows selection of frames depicting the maximum (end-diastolic) and minimum (end-systolic) ventricular volumes. The ejection fraction (EF) is then calculated as follows15,16:
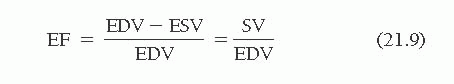
Table 21.1 Regression Equations to Correct for Overestimation in Calculation of Left Ventricular Volumes | ||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ||||||||||||||||||||||||||||||||
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree