Chapter 1
Epidemiology and Clinical Analysis
Louis L. Nguyen, Ann DeBord Smith
The goal of this chapter is to introduce the vascular surgeon to the principles that underlie the design, conduct, and interpretation of clinical research. Disease-specific outcomes otherwise detailed in subsequent chapters will not be covered here. Rather, this chapter discusses the historical context, current methodology, and future developments in epidemiology, clinical research, and outcomes analysis. This chapter serves as a foundation for clinicians to better interpret clinical results and as a guide for researchers to further expand clinical analysis.
Epidemiology
Epidemiology is derived from the Greek terms for “upon” (epi), “the people” (demos), and “study” (logos), and can be translated into “the study of what is upon the people.” It exists to answer the four major questions of medicine: diagnosis, etiology, treatment, and prognosis.
Brief History
Hippocrates is considered to be among the earliest recorded epidemiologists because he treated disease as both a group event and an individual occurrence. His greatest contribution to epidemiology was the linkage of external factors (climate, diet, and living conditions) with explanations for disease. Before widespread adoption of the scientific method, early physicians inferred disease causality through careful observation. For example, they observed the geographic distribution of cases or common factors shared by diseased versus healthy persons. John Snow is recognized for ameliorating the cholera epidemic in the Soho district of London in 1854 by identifying the cause of the outbreak through mapping the location of known cases of cholera in the district. Based on the density and geographic distribution of cases, he concluded that the public water pump was the source and had the pump handle removed.1
Modern Developments
Modern epidemiology and clinical analysis seek to establish causation through study design and statistical analysis. Carefully designed studies and analyses can minimize the risk of false conclusions and maximize the opportunity to find causation when it is present. In other areas of biology, causation can be demonstrated by fulfilling criteria, such as Koch’s postulates for establishing the relationship between microbe and disease. In epidemiology, the study design that would offer ideal proof of causation would be comparison of people with themselves in both the exposed and the unexposed state. This impossible and unethical experiment would control for everything, except the exposure, and thus, establish the causality between exposure and disease. Because this condition cannot exist, it is referred to as counterfactual. Because the ideal study is impossible to conduct, alternative study designs have developed with different risks and benefits. The crossover experimental design, for example, approaches the counterfactual ideal by exposing patients to both treatment groups in sequence. However, the influence of time and previous exposure to the other treatment assignment may still affect the outcome (also known as the carryover effect). Other study designs exist that include techniques such as randomization or prospective data gathering to minimize bias. Appropriate study design must be selected based upon a study’s objectives. After a study is complete, conclusions can be drawn from a carefully crafted statistical analysis. Modern epidemiology includes applied mathematical methods to quantify observations and draw inferences about their relationships.
Evidence-based medicine is a relatively modern approach to the practice of medicine that aims to qualify and encourage the use of currently available clinical evidence to support a particular treatment paradigm. This practice encourages the integration of an individual practitioner’s clinical expertise with the best currently available recommendations from clinical research studies.2 Relying on personal experience alone could lead to biased decisions, whereas relying solely on results from clinical research studies could lead to inflexible policies. Evidence-based medicine stratifies the strength of the evidence from clinical research studies based on study design and statistical findings (Table 1-1). The criteria differ when the evidence is sufficient to support a specific therapeutic approach, prognosis, diagnosis, or other health services research. Criteria also differ among research institutions, including the U.S. Preventive Services Task Force and the U.K. National Health Service. However, common themes can be seen among the different fields. Systematic reviews with homogeneity are preferred over single reports, whereas randomized controlled trials (RCTs) are preferred over cohort and case-control studies. Even within similar study design groupings, the statistical strength of each study is evaluated, with preference for studies with large numbers, complete and thorough follow-up, and results with small confidence intervals. Clinical recommendations are then based on the available evidence and are further graded according to their strengths (Table 1-2).
Table 1-1
Levels of Evidence for Therapeutics
| Level | Evidence |
| 1a | Systematic reviews of RCT studies with homogeneity |
| 1b | Individual RCT with narrow confidence intervals |
| 1c | “All or none” trials* |
| 2a | Systematic reviews of cohort studies with homogeneity |
| 2b | Individual cohort studies |
| 2c | Clinical outcomes studies |
| 3a | Systemic reviews of case-control studies with homogeneity |
| 3b | Individual case-control studies |
| 4 | Case-series studies |
| 5 | Expert opinion without critical appraisal or based on bench research |
* In which all patients died before the therapeutic became available, but some now survive with it, or in which some patients survived before the therapeutic became available, but now none die with it.
RCT, Randomized controlled trial.
Adapted from Oxford Centre for Evidence-based Medicine (2001).
Table 1-2
Grades of Recommendation
| Grade | Recommendation | Basis |
| A | Strong evidence to support practice | Consistent level 1 studies |
| B | Fair evidence to support practice | Consistent level 2 or 3 studies or extrapolations from level 1 studies |
| C | Evidence too close to make a general recommendation | Level 4 studies or extrapolation from level 2 or 3 studies |
| D | Evidence insufficient or conflicting to make a general recommendation | Level 5 evidence or inconsistent studies of any level |
Adapted from U.S. Preventive Services Task Force Ratings (2003) and Oxford Centre for Evidence-based Medicine (2001).
Clinical Research Methods
Although measuring the incidence and prevalence of disease is useful in the initial understanding of a disease process, additional techniques must be used to identify risk factors and test treatments for disease. The choice of study design and statistical analysis technique depends on the available data, the hypothesis being tested, and patient safety and/or ethical concerns.
Study Design
Clinical research can be broadly divided into observational studies and experimental studies. Observational studies are characterized by the absence of a study-directed intervention, whereas experimental studies involve testing a treatment, be it a drug, a device, or a clinical pathway. Observational studies can follow ongoing treatments but cannot influence choices made in the treatment of a patient. Observational studies can be executed in a prospective or retrospective fashion, whereas experimental studies can be performed only prospectively.
Two factors that affect choice of study design include prevalence and incidence of disease. The prevalence of disease is the ratio of persons affected for the population at risk and reflects the frequency of the disease at the measured time point, regardless of the time of disease development. In contrast, the incidence is the ratio of persons in whom the disease develops within a specified period for the population at risk. For diseases with short duration or high mortality, prevalence may not accurately reflect the impact of disease because the single time point of measurement does not capture resolved disease or patients who died of the disease. Prevalence is a more useful parameter when discussing diseases of longer duration, whereas incidence is more useful for diseases of shorter duration.
Observational Studies
There are two main types of observational studies: cohort and case-control studies. A cohort is a designated group of individuals that is followed over a period of time. Cohort studies seek to identify a population at risk for the disease of interest. After a period of observation, patients in whom the disease develops are compared with the population of patients who are free of the disease. Cohort studies are most often associated with epidemiology because they comprise many of the most prominent studies in the modern era. The classic example is the Framingham Heart Study (FHS), in which 5209 residents of Framingham, Massachusetts, were monitored prospectively, starting in 1948.3 Much of our epidemiologic knowledge regarding risk factors for heart disease comes from the FHS.4 Although the FHS was initially intended to last 20 years, the study has subsequently been extended and now involves the third generation of participants. Cohort studies also seek to identify potential risk factors for development of the disease of interest. For example, if cigarette smoking is suspected in the development of peripheral arterial disease (PAD), smokers are assessed for the development of PAD from the beginning of the observation period to the end of the observation period. Because PAD does not develop in all smokers, and conversely, not all PAD patients are smokers, a relative risk (RR) is calculated as the ratio of the incidence of PAD in smokers versus the incidence of PAD in nonsmokers.
The main challenge in case-control studies is to identify an appropriate control group with characteristics similar to those of the general population at risk for the disease. Inappropriate selection of the control group may lead to the introduction of additional confounding and bias. For example, matched case-control studies aim to identify a control group “matched” for factors found in the exposure group. Unfortunately, by matching even basic demographic factors, such as gender and the prevalence of comorbid conditions, unknown co-associated factors can also be included in the control group and may affect the relationship of the primary factor to the outcome. Appropriate selection of the control group can be achieved by using broad criteria, such as time, treatment at the same institution, age boundaries, and gender when the exposure group consists of only one gender.
Experimental Studies
Experimental studies differ from observational studies in that the former expose patients to a treatment being tested. Many experimental trials involve randomization of patients to the treatment group or appropriate control group. Although randomization ensures that known factors are evenly distributed between the exposure and control groups, the importance of RCTs lies in the even distribution of unknown factors. Thus, a well-designed RCT will result in more simplified endpoint analyses because complex statistical models are not necessary to control for confounding factors.
Randomization can be accomplished by complete randomization of the entire study population, by block randomization, or by adaptive randomization. For complete randomization, each new patient is randomized without prior influence on previously enrolled patients. The expected outcome at the completion of the trial is an equal distribution of patients within each treatment group, although unequal distribution may occur by chance, especially in small trials. Block randomization creates repeated blocks of patients in which equal distribution between treatment groups is enforced within each block. Block randomization ensures better end randomization and periodic randomization during the trial. End randomization is important in studies with long enrollment times or in multi-institutional studies that may have different local populations. Because the assignment of early patients within each block influences the assignment of later patients, block randomization should occur in a blinded fashion to avoid bias. Intrablock correlation must also be tested in the final analysis of the data. Adaptive randomization seeks to achieve balance of assignment of randomization for a prespecified factor (e.g., gender or previous treatment) suspected of affecting the treatment outcome. In theory, randomization controls for these factors, but unique situations may require stricter balance.
RCTs can be classified according to knowledge of the randomization assignment by the treating clinicians and their patients. In open trials, the clinician and patients know the full details of the treatment assignment. This leaves the potential for bias in interpretation of results and may also influence study patients to drop out if they are randomized to a treatment group that they perceive to be unfavorable. Open trials are often conducted for surgical patients, where it is not possible or ethical to conceal the treatment assignment from the patient or the provider. In single-blinded trials, the clinician is aware of the treatment assignment, but the patient is not. These studies have more effective controls, but are still subject to clinician bias. Double-blinded trials are conducted so that both clinicians and patients are unaware of the treatment assignment. Often, a separate research group is responsible for the randomization allocation and has minimal or no contact with the clinicians and patients.
Experimental studies face stricter ethical and patient safety requirements than their observational counterparts. To expose patients to randomization of treatment, clinical equipoise must exist. The principle of equipoise relies on a situation in which clinical experts professionally disagree on the preferred treatment method.5 Thus, randomization of study patients to different treatments is justified to gain clinical information. Ideally, the patients being tested or their population counterparts would benefit from any medical knowledge gained from the study. It is worth noting that although the field may have equipoise, individual health care providers or patients may have bias for one treatment. In such a case, enrollment in an RCT may be difficult because the patients or their providers are not willing to be subject to randomization.
Although RCTs represent the pinnacle in clinical design, there are many situations in which RCTs are impractical or impossible. Clinical equipoise may not exist, or common sense may prevent randomization of well-established practices, such as the use of parachutes.6 RCTs are also costly to conduct and must generate a new control group with each trial. For this reason, some studies are single-arm trials that use historical controls similar to the case-control design. In addition, patient enrollment for RCTs is more difficult than for other trial designs because some patients and clinicians are uneasy with the randomization of treatment. They may have preconceived notions of treatment efficacy or may have an inherent aversion to being randomized, even when they know that equipoise exists. This risk aversion may be greatest for more life-threatening conditions, although patients in whom conventional treatment has been unsuccessful may be accepting of greater risk to obtain access to novel treatments otherwise not available outside the clinical trial. RCTs can also have methodological and interpretative limitations. For example, study patients are analyzed by their assigned randomization grouping (intent to treat). Studies with asymmetric or numerous overall dropout and/or crossover rates will not reflect actual treatment effects. RCTs are often conducted in high-volume specialty centers; as a result, enrollment and treatment of study patients may not reflect the general population with the disease. Finally, RCTs are often designed and powered to test one hypothesis. A statistically nonsignificant result may be influenced by inaccurate assumptions made in the initial power calculations.
Special Techniques: Meta-Analysis
Meta-analysis is a statistical technique that combines the results of several related studies to address a common hypothesis. The first use of meta-analysis in medicine is attributed to Smith and Glass in their review of the efficacy of psychotherapy in 1977.7 By combining results from several smaller studies, researchers may decrease sampling error, increase statistical power, and thereby help clarify disparate results among different studies.
The related studies must share a common dependent variable along with the effect size specific to each study. The effect sizes are not merely averaged among the studies, but are weighted to account for the variance in each study. Because studies may differ in patient selection and their associated independent variables, a test for heterogeneity should also be performed. Where no heterogeneity exists (P > .5), a fixed-effects meta-analysis model is used to incorporate the within-study variance for the studies included, whereas a random-effects model is used when concern for between-study variance exists (.5 > P > .05). When heterogeneity among studies is found, the OR should not be pooled, and further investigation for the source of heterogeneity may then exclude outlying studies.
The weighted composite dependent variable is visually displayed in a forest plot along with the results from each study included. Each result is displayed as a point estimate with a horizontal bar representing the 95% confidence interval for the effect. The symbol used to mark the point estimate is usually sized proportional to other studies to reflect the relative weight of the estimate as it contributes to the composite result (Fig. 1-1). Classically, meta-analyses have included only RCTs, but observational studies can also be used.8,9 Inclusion of observational studies can result in greater heterogeneity through uncontrolled studies or controlled studies with selection bias.
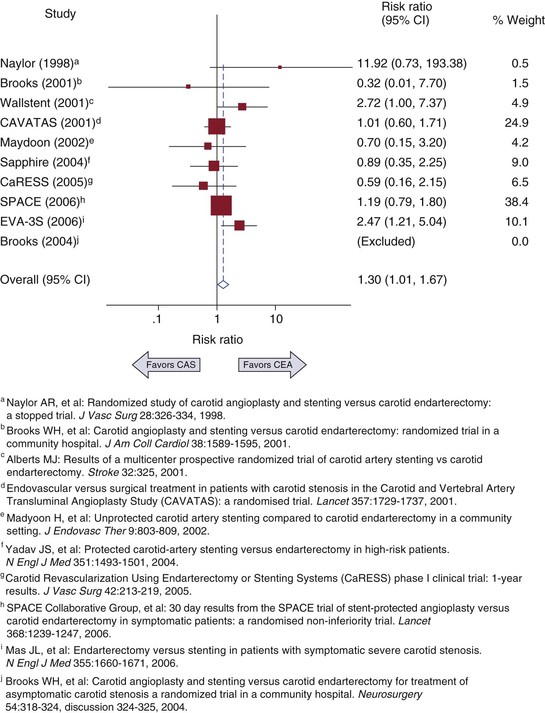
Figure 1-1 Example of a forest plot from a meta-analysis of carotid artery stenting (CAS) versus carotid endarterectomy (CEA) to determine 30-day risk for stroke and death. CI, Confidence interval. (Redrawn from Brahmanandam S, et al: Clinical results of carotid artery stenting compared with endarterectomy. J Vasc Surg 47:343-349, 2008.)
The strength of a meta-analysis comes from the strength of the studies that make up the composite variable. Furthermore, if available, the results of unpublished studies can also potentially influence the composite variable, because presumably many studies with nonsignificant results are not published. Therefore, an assessment of publication bias should be included with every meta-analysis. Publication bias can be assessed graphically by creating a funnel plot in which the effect size is compared with the sample size or other measure of variance. If no bias is present, the effect sizes should be balanced around the population mean effect size and decrease in variance with increasing sample size. If publication bias exists, part of the funnel plot will be sparse or empty of studies. Begg’s test for publication bias is a statistical test that represents the funnel plot’s graphic test.10 The variance of the effect estimate is divided by its standard error to give adjusted effect estimates with similar variance. Correlation is then tested between the adjusted effect size and the meta-analysis weight. An alternative method is Egger’s test, in which the study’s effect size divided by its standard error is regressed on 1/standard error.11 The intercept of this regression should equal zero, and testing for the statistical significance of nonzero intercepts should indicate publication bias.
Bias in Study Design
Clinical analysis is an attempt to estimate the “true” effects of a disease or its potential treatments. Because the true effects cannot be known with certainty, analytic results carry potential for error. All studies can be affected by two broadly defined types of error: random error and systematic error. Random error in clinical analysis comes from natural variation and can be handled with the statistical techniques covered later in this chapter. Systematic error, also known as bias, affects the results in one unintended direction and can threaten the validity of the study. Bias can be further categorized into three main groupings: selection bias, information bias, and confounding.
Selection bias occurs when the effect being tested differs among patients who participate in the study as opposed to those who do not. Because actual study participation involves a researcher’s determination of which patients are eligible for a study and then the patient’s agreement to participate in the study, the decision points can be affected by bias. One common form of selection bias is self-selection, in which patients who are healthier or sicker are more likely to participate in the study because of perceived self-benefit. Selection bias can also occur at the level of the researchers when they perceive potential study patients as being too sick and preferentially recruit healthy patients.
Information bias exists when the information collected in the study is erroneous. One example is the categorization of variables into discrete bins, as in the case of cigarette smoking. If smoking is categorized as only a yes or no variable, former smokers and current smokers with varying amounts of consumption will not be accurately categorized. Recall bias is another form of information bias that can occur particularly in case-control studies. For example, patients with abdominal aortic aneurysms may seemingly recall possible environmental factors that put them at risk for the disease. However, patients without aneurysms may not have a comparable imperative to stimulate memory of the same exposure.
Confounding is a significant factor in epidemiology and clinical analysis. Confounding exists when a second spurious variable (e.g., race/ethnicity) correlates with a primary independent variable (e.g., type 2 diabetes) and its associated dependent variable (e.g., critical limb ischemia). Researchers can conclude that patients in certain race/ethnicity groups are at greater risk for critical limb ischemia when diabetes is actually the stronger predictor. Confounding by indication is especially relevant in observational studies. This can occur when, without randomization, patients being treated with a drug can show worse clinical results than untreated counterparts because treated patients were presumably sicker at baseline and required the drug a priori. Confounding can be addressed by several methods: assigning confounders equally to the treatment and control groups (for case-control studies); matching confounders equally (for cohort studies); stratifying the results according to confounding groups; and multivariate analysis.
Outcomes Analysis
As physicians, we can usually see the natural progression of disease or the clinical outcome of treatment. Although these observations can be made for individual patients, general inferences about causation and broad application to all patients cannot be made without further analysis. Clinical analysis attempts to answer these questions by either observing or testing patients and their treatments. Because clinical analysis can be performed only on a subset or sample of the relevant entire population, a level of uncertainty will always exist in clinical analysis. Statistical methods are an integral aspect of clinical analysis because they help the researcher understand and accommodate the inherent uncertainty in a sample in comparison to the ideal population. In the following sections, common clinical analytic methods are reviewed so that the reader can better interpret clinical analysis and also have foundations to initiate an analysis. Reference to biostatistical and econometric texts is recommended for detailed derivation of the methods discussed.
Statistical Methods
At the beginning of most clinical analyses, descriptive statistics are used to quantify the study sample and its relevant clinical variables. Continuous variables (such as weight or age) are expressed as means or medians; categorical variables (such as the Trans-Atlantic Society Consensus [TASC] Classification: A, B, C, or D) are expressed as numbers or percentages of the total. Study sample characteristics and their relative distribution of comorbid conditions help determine whether the sample is consistent with known population characteristics, and hence, addresses the issue of generalizability of the clinical results to the overall population.
The next step in clinical analysis is hypothesis testing, in which the factor or treatment of interest is tested against a control group. The statistical methods used in hypothesis testing depend on the research question and characteristics of the data under comparison (Box 1-1). At its core, hypothesis testing asks whether the observable differences between groups represent a true difference or an apparent difference attributable to random error. A variety of statistical tests are available to accommodate the types of data being analyzed.



