Computational Representation of the Electromechanical Processes in the Heart

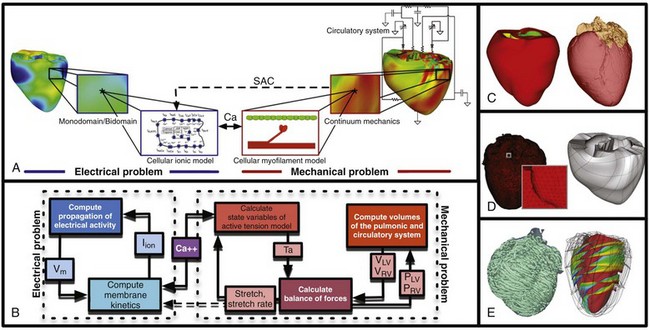
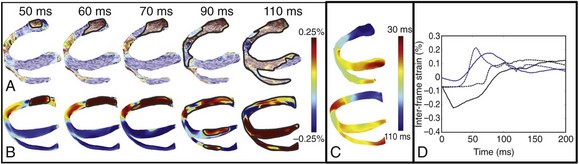
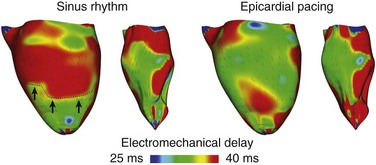
A schematic of the general approach to modeling multi-scale cardiac electromechanical function at the level of the organ is shown in Figure 36-1, A. The general approach consists of two coupled problems, simulating the electrical and mechanical functions of the heart. A flowchart of the simulation process with connections within the model representation of each function as well as inter-relations between the two parts of the electromechanical model is presented in Figure 36-1, B.

The electrical problem of the model simulates the propagation of a wave of transmembrane potential by solving the monodomain reaction-diffusion partial differential equation (PDE; or a system of coupled PDEs if the extracellular current flow is explicitly accounted for, i.e., the bidomain problem) over the volume of the heart.¹ The reaction-diffusion PDE describes current flow through myocytes that are electrically connected via low-resistance gap junctions. Cardiac tissue has orthotopic passive electrical conductivities that arise from the cellular organization of the heart into fibers and laminar sheets. Global conductivity values are obtained by combining fiber and sheet organization with myocyte-specific local conductivity values. Current flow in the tissue is driven by the active processes of ionic exchanges across myocyte membranes. These processes are represented by the cellular ionic model (see Figure 36-1, A, B), where current flow through ion channels, pumps, and exchangers and subcellular calcium cycling are governed by a set of ordinary differential (ODE) and algebraic equations; ionic models of different complexity are currently in use.² Simultaneous solution of the PDE(s) with the set of ionic model equations represents simulation of electrical wave propagation in the heart.

The intracellular calcium released during electrical activation couples the electrical and mechanical components of the model by providing a bi-directional link between the cellular ionic and myofilament models (see Figure 36-1, A, B). The cellular myofilament model consists of another set of ODEs that represent the biophysical processes of calcium binding to troponin and cross-bridge cycling, as well as the mechanisms of cooperativity. Compared with the evolution of cellular ionic models, the development of myofilament models has been slower and more difficult, as no clear consensus has been reached regarding the mathematical approach to model myofilament dynamics. An up-to-date review of cellular myofilament models can be found in a recent publication.³

The contraction of the heart arises from the active tension generated by the myofilaments within the cardiac cell. In the mechanics part of the model, deformation of the organ is described by the equations of continuum mechanics,⁴ with the passive properties of the myocardium described by a constitutive law. The most comprehensive formulation of cardiac tissue constitutive relation can be found in a recent article by Holzapfel and Ogden.⁵ Simultaneous solution of the myofilament model equations and of those representing passive cardiac mechanics over the volume of the heart (see Figure 36-1, A, B) constitutes simulation of cardiac contraction. Finally, to simulate the cardiac cycle and the corresponding pressure-volume loops, conditions on chamber volume and pressure are imposed, arising typically from lumped-parameter models of the systemic and pulmonic circulatory systems (see Figure 36-1, A, B).

In addition to the bi-directional relationship between electrical and mechanical components, provided by intracellular calcium cycling, a key feedback mechanism in the electromechanical model (acting within the mechanics component) is the length and velocity dependence of tension (see Figure 36-1, B): The stretch and stretch rate, as determined by the deformation of the heart, affect tension development in the cell. Mechanical deformation could further affect the electrical activity of the heart via the opening of stretch-activated channels (see Figure 36-1, A, B). To simulate this feedback mechanism, the stretch and stretch rate calculated from the mechanics component serve as an input into the electrical component: They determine the conductance of stretch-activated channels, the latter represented within the cellular ionic model.

Solutions to organ-level electromechanical problems entail the use of organ-level geometries, which could be idealized (such as cylindrical and elliptical shapes to represent the ventricles) or anatomically accurate, the latter representing ventricular averaged geometries obtained from histologic sectioning6–8 or the geometry and structure of individual hearts,^9–11 as obtained from magnetic resonance imaging (MRI).¹² Figure 36-1, C presents some of the ventricular geometries used in electromechanical modeling: The University of California San Diego (UCSD) rabbit ventricular geometry⁶ is an example of averaged geometry obtained through histologic sectioning, while another image exemplifies an MRI-based individual heart geometry.⁹ An example of an MRI-based atrial geometry only can be found in a recent publication.¹³

The aforesaid description of electromechanical modeling refers to models of strong coupling, where the electrical and mechanical problems are solved simultaneously.¹⁴ In cases that do not necessitate strong coupling, as for instance during examination of how the mechanical activation of the heart follows the electrical activation, weakly coupled schemes are employed. In a weakly coupled model, the electrical activation times (calculated from the electrical problem) are inputted into the mechanical part as the instances when the myofilament model is activated. In a more sophisticated approach, the ionic and cardiac myofilament models can be coupled within the mechanics component, with the electrical activation times determining the instant at which this combined ionic-myofilament model is activated¹⁰; in this case, cooperativity mechanisms, such as calcium binding to troponin C, are represented in the model.

The governing equations describing cardiac electromechanical behavior are solved on a spatially discretized version of the heart volume (i.e., on the computational mesh). The electrical and mechanical parts of the model have different requirements regarding the degree of discretization (i.e., element size) and the element type; thus the two parts of the model require two different computational meshes. The electrical mesh requirements are based on spatiotemporal characteristics of wave propagation; a spatial resolution of about 250 to 300 micrometers is appropriate for electrophysiological finite element models. A novel approach was recently published for electrical mesh generation directly from segmented MRI¹⁵ (Figure 36-1, D). The mechanical mesh, on the other hand, typically consists of hexahedral elements with a Hermite basis. This choice of finite elements increases the degree of strain continuity and is appropriate for maintaining incompressibility constraints. The mechanical mesh of the heart (see Figure 36-1, D) can also be generated directly from segmented MRI.^10,16

Fiber and laminar sheet organization underlies the orthotropic electrical conductivities of the tissue and its mechanical properties. In the electrical mesh, local fiber and sheet directions are typically mapped at the centroids of the finite elements, and in the mechanics mesh, fiber and sheet orientations and their derivatives are defined at mesh nodes and then are interpolated over the elements. This is typically done using histologic sectioning information⁶ or diffusion tensor (DT) MRI data.^9,10 Use of DT-MRI data is based on the fact that the primary, secondary, and tertiary eigenvectors of the water DTs are aligned with fiber direction, with the direction transverse to the fiber direction and in the plane of the laminar sheet, and with that normal to the laminar sheet, respectively.¹² Figure 36-1, E presents fiber and sheet orientation, as reconstructed from DT-MRI of the canine heart. In cases where neither histologic nor DT-MRI information is available, rule-based approaches¹⁷ or image transformation algorithms¹⁸ have been used to assign fiber and sheet orientation consistent with measurements.

Simulations of heart electromechanical function are typically executed on parallel high-performance computing hardware. Reviews of numeric approaches to simulating the electromechanical activity of the heart can be found1,10,19,20; these articles also address the challenges involved in developing multi-scale models at the organ level.

Approaches to Experimental Validation of Electromechanical Models

Validating the ventricular (or atrial) model of cardiac electromechanics with experimental data is a pivotal component of model development. It constrains the model parameter space and enhances the physiological relevance of the model. To validate the electrical component of the model, simulation results are often compared with electrical activation maps obtained from epicardial sock or plunge electrodes, from optical mapping, or from electrocardiograms (ECGs) and body surface potential maps. The mechanical component is validated with local strain measurements calculated from MRI or ultrasound images, or with hemodynamical metrics such as left ventricular (LV) pressure and volume, ejection fraction, or maximal rate of pressure change.

A study by Provost et al²¹ provides a unique example of electromechanical (rather than separate electrical or mechanical) heart model validation. It is based on the use of electromechanical wave imaging (EWI),²² a novel noninvasive ultrasound-based imaging technique capable of mapping the propagation of the electromechanical wave along echocardiographic planes; this is achieved by mapping the interframe axial strains. In the Provost et al study,²¹ data from EWI were used to validate the MRI-based electromechanical model of the normal canine ventricles for different pacing protocols. Figure 36-2, A, B presents experimental and simulated EWI maps for pacing from the LV base; the corresponding isochronal maps of electromechanical activation are shown in Figure 36-2, C. In both experiments and simulations, the EW emerged from the basal region of the lateral wall and propagated toward the apex, the septum, and the right ventricular (RV) wall. Representative curves of the interframe strains over time in the lateral and septal wall are shown in Figure 36-2, D. This study provides an illustrative example of how emerging experimental techniques like EWI could be used for validation of cardiac electromechanical models.

Electromechanical Interactions in the Heart

Understanding the mechanical consequences of an altered cardiac activation sequence is of great importance because dyssynchronous electrical activation can cause abnormalities in perfusion and pump function. Early computational studies of electromechanics employed truncated ellipsoids as LV representations in an attempt to provide insight into the relationship between the spatial pattern of electrical activation and the resultant contraction.²³ The study by Usyk and McCulloch²⁴ was the first to examine the distribution of the time interval between myocyte depolarization and onset of myofiber shortening, termed the electromechanical delay, in a realistic-geometry ventricular canine model. The study by Gurev et al²⁵ further advanced understanding of the three-dimensional (3D) electromechanical delay distribution in the intact ventricles for sinus rhythm and epicardial pacing. The authors employed an electromechanical model of the rabbit ventricles and dissected the role of loading conditions in altering the 3D distribution of electromechanical delay. Figure 36-3 presents the epicardial and endocardial electromechanical delay distributions for sinus rhythm and epicardial pacing obtained in the study. Results revealed that during normal sinus rhythm, the electromechanical delay was longer on the epicardium than on the endocardium and at the base than at the apex. After epicardial pacing, electromechanical delay distribution was markedly different. For both electrical activation sequences, the late-depolarized regions were characterized by significant myofiber prestretch caused by contraction of the early-depolarized regions. This prestretch delayed the onset of myofiber shortening, thus resulting in a longer electromechanical delay, giving rise to heterogeneities in 3D electromechanical delay distribution. This study underscored the central role that the electrical activation sequence and thus the loading conditions play in modulating the relationship between electrical activation and mechanical contraction.

Stay updated, free articles. Join our Telegram channel

Join