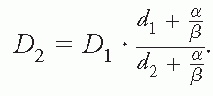Biological Basis of Fractionation and Timing of Radiotherapy
Dirk De Ruysscher
Vincent S. Khoo
Søren M. Bentzen
THE BIOLOGY OF DOSE FRACTIONATION IN RADIOTHERAPY
Radiation biology is the study of the biological effects of ionizing radiation; clinical radiation biology is concerned with the clinical response of human tumors and normal tissues to the doses normally used in radiation therapy. Basic and clinical radiation biology together form the scientific basis for application of radiation as an anticancer agent and provide the framework for understanding dose-fractionation and dose-volume effects as well as the rational basis for combining radiation with cytotoxic or molecular targeted agents.
Although advances in molecular radiation biology of tumors1,2 and normal tissue3 play an increasingly important role in further developing the scientific basis for radiation therapy, the conceptual basis for dose fractionation is still, to a large extent, rooted in the target-cell hypothesis, that is, the hypothesis that the main biological effect of ionizing radiation on cells and tissues is direct cell killing and loss of proliferative capacity of surviving cells. Therefore, much of the current chapter describes dose-fractionation effects within the target-cell framework, often referred to as “classical radiobiology.” However, the more recent thinking in the field will be brought in, where this is relevant for understanding some of the newer trends in radiation dose fractionation.
The Physical-Biological Interactions of Radiation
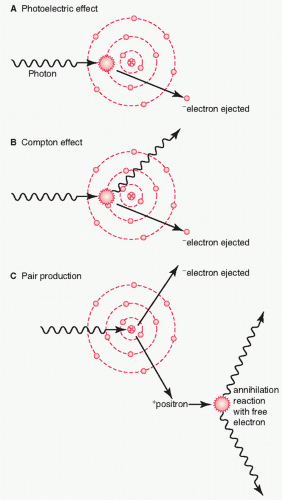
The basic interaction of radiation with matter has been well understood since the first third of the 20th century. When a radiation beam traverses through matter, energy is deposited along its path. Compton scattering is the dominating interaction for radiation beam energies used clinically (Fig. 41.1). The Compton effect is an inelastic scattering of photons by an electron (i.e., the photon loses some of its energy in the event), leading to ionization events either within the molecules of the critical cells (direct effect) or in adjacent water molecules (indirect effect).4 These direct and indirect effects result in the formation of unstable and highly reactive free radicals that are responsible for the biological effects on DNA and tissues. Cellular damage and cell killing occurs when critical molecular target(s) such as DNA are damaged within the cell.5 Cancer cell killing can be defined as the loss of the cell’s reproductive ability. Most cells do not die immediately when they are critically damaged. They usually proceed to mitosis and either may fail to complete mitosis or may progress through one or more cycles before failing at a subsequent mitosis. However, some cell types, such as lymphocytes, die before reaching mitosis in a process called apoptosis or “programmed cell death.”6 In the apoptotic process, the radiation damage initiates signaling cascades, whereby preset mechanisms are evoked to cause cellular self-destruction. Characteristic histological features are seen in apoptotic cells such as blebbing and fragmentation of the nucleus.7
In addition to the “direct-targeted” effects of ionizing radiation on cells, there is increasing evidence for nontargeted effects of radiation such as bystander cell killing.8 The therapeutic implications, if any, of this mode of cell killing are not well understood.
The Cell Survival Curves The target cell hypothesis postulates that the response of tumors and normal tissues to ionizing radiation is a direct result of the loss of reproductive ability of the irradiated cells. This can be assessed in vitro by the ability of cells in culture to continue sustained cellular division to form a colony. A plot of the colony-forming ability of cells as a function of dose is called a cell survival curve. The parameters that influence cell survival curves will be described later in this chapter. 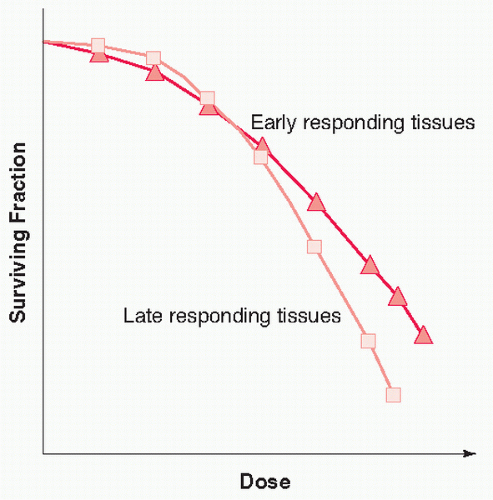The cell survival curve was first described by Puck and Marcus9 in 1956, who examined the survival of HeLa tumor cells as a function of radiation dose. The cell survival curve shape for early-and late-reacting tissues (see discussion that follows) is represented in Figure 41.2, in which the cell’s survival fraction is plotted against dose on a semilogarithmic scale. In general, at very low radiation doses, the cell survival curve is relatively shallow, whereas at higher doses, the survival curve bends more, reflecting the greater cell kill per unit Gu as dose
increases. This shape of the cell survival curve with an initial shallow slope followed by a “broad-shoulder” curve is typical of low-linear energy transfer (LET) radiation (e.g., photons, which are commonly used for lung radiotherapy). In contrast, cell survival curves for high LET radiation, such as neutrons and12 C-ions have very little “shoulder” but are approximately straight lines in semilogarithmic coordinates.
increases. This shape of the cell survival curve with an initial shallow slope followed by a “broad-shoulder” curve is typical of low-linear energy transfer (LET) radiation (e.g., photons, which are commonly used for lung radiotherapy). In contrast, cell survival curves for high LET radiation, such as neutrons and12 C-ions have very little “shoulder” but are approximately straight lines in semilogarithmic coordinates.
 FIGURE 41.1 Radiation tissue interaction effects. A: The photoelectric effect occurs when the incident photon strikes one of the bound inner shell electrons around the atomic nucleus and transfers its entire energy to the electron, causing the electron to be ejected from its orbit. This electron may then collide with other orbiting electrons and result in a chain of further strikes, electron expulsion, ionization, and other collisions. The incident photon disappears when its energy is used up. B: Compton process differs from the photoelectric effect in that only a portion of the energy of the incident photon is used in ejecting the orbiting electron, and the remaining energy is emitted in a secondary photon of less energy. This secondary photon can subsequently cause further ionization either through the photoelectric or Compton process. C: Pair production process is the least common therapeutic method of energy absorption. This only occurs when an incident photon interacts with an atomic nucleus and its energy is completely transformed into two particles (a positron and an electron). These two particles do not come from the atom, so no single charged particle has been lost; therefore, there is no ionization of the atom. The positron can then react with an orbital electron of another atom resulting in an “annihilation” reaction producing two photons of 0.51 MeV. For this process to occur, the initial incident photon must have energy of least 1.02 MeV. A pair production chain reaction never results because the annihilation photons never have energy greater than 0.51 MeV. (From Khoo V, Bidmead M. Chapter 1. Physical basis of radiotherapy. In: Huddart RA, Murthy V, eds. Cancer Radiotherapy: Methods and Protocols. Clifton, New Jersey, Humana Press, 2007.) |
Several mathematical models have been devised to describe the cell survival curve shape. Of these models, the most widely adopted is the linear-quadratic model10 that appears to provide the best description of cell survival within the range of doses used clinically. The linear-quadratic equation is expressed mathematically as follows:
where S = survival of a cell population after a dose of radiation (d) and where α and β are constants. Assuming that the effect per fraction is constant, it is easily shown that the effect of n fractions of size d is:
where D = nd is the total dose after n fractions. It follows from this equation that a total dose D1 delivered with dose per fraction d1, will result in the same biological effect as a total dose D2 delivered with dose per fraction d2 if (and only if):
This equation is known as Withers’ formula.11 This formula can be interpreted operationally as a means of adjusting for dose per fraction—irrespective of any underlying mechanistic interpretation at the cellular level. It can be seen from the mathematical form of Withers formula that it is the ratio between α and β, rather than the parameter values themselves,
which determines the change in total dose as a function of a change in dose per fraction that will be required to maintain the same level of biological effect.
which determines the change in total dose as a function of a change in dose per fraction that will be required to maintain the same level of biological effect.
 FIGURE 41.2 The dose-survival curves for early-and late-responding tissues. The cell survival curve for late-responding tissues is more “curvy” than for early-responding tissues and at least some cancer types. The α / β ratio is approximately 2 Gy for late-responding tissues and 10 Gy for some cancers or early-responding tissues. |
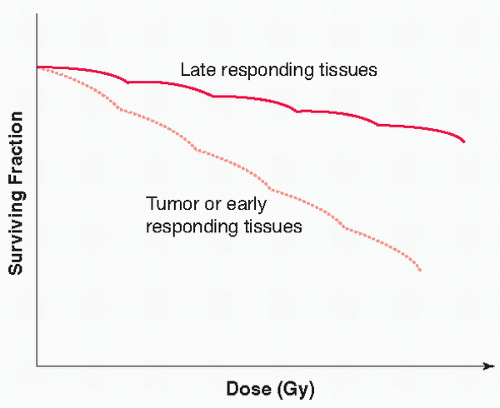
The α / β ratio will be specific to different normal-tissue side effects and can be seen, as mentioned previously, as a measure of fractionation sensitivity of an end point.12 Early side effects are generally characterized by a high α / β ratio, in the order of 10 Gy, and these occur, for example, in the gastrointestinal epithelium, skin, and bone marrow (Fig. 41.2). Late end points such as radiation myelopathy or radiation-induced fibrosis will typically have a low α / β ratio in the range from 1 to 5 Gy (Fig. 41.2). There are relatively sparse data on α /β for human tumors, but it is often assumed that it is in the same range as for early normal-tissue effects of radiation.
This differential in fractionation sensitivity between, at least, some human tumors and some types of late-occurring side effects of radiotherapy provides a rationale for dividing the total prescribed radiation dose into many smaller doses delivered over a period of time. This difference has been exploited by investigators using altered fractionation schemes to manipulate the therapeutic ratio in favor of improved tumor control while reducing damage to normal structures or late-responding tissues. A good example of this fractionation strategy is the development of the continuous hyperfractionated accelerated radiotherapy (CHART) regime in lung cancer.13,14
The Four R’s of Radiotherapy Several biological parameters influence the response of both normal tissues and cancers cells to fractionated radiotherapy. Following Withers,15 these are memorized as the four R’s of radiotherapy: Repair, Redistibution, Repopulation, and Reoxygenation. All of these are processes taking place in the interval between fractions, and the differential between tumors and normal tissues in these four R’s form the classical rationale for dose fractionation as well as the “Radiosensitivity” of cells/tissues. Steel16 subsequently advocated to add this fifth R, namely Radiosensitivity, as a cofactor in determining cellular response to radiation. However, this R is clearly of a different nature than the original four R’s. These R’s of radiotherapy are summarized in Table 41.1 and will briefly be described in the following.
Repair Both normal and cancer cells show split-dose recovery, expressed as a higher in vitro cell survival if the same physical dose is split in two, with a sufficient time interval between irradiations. This phenomenon is thought to reflect chemical and enzymatic repair of DNA damage in the interval between doses.17
The clinical implication of this is that if multiple fractions are being given within a single day, then there must be an adequate time interval given between fractions (minimum 6 hours, preferably 8 or 10 hours) in order to permit repair of sublethal damage. As previously mentioned, the shoulder of the cell survival curve is repeated for each dose fraction as shown in Figure 41.3, provided that cellular recovery is complete between fractions. The broader the shoulder, the greater the repair capacity of the cells. This is in particular seen in late-responding tissues with low α / β ratios. These tissues can be spared from accumulating radiation DNA damage by fractionation.
In general, these repair processes will affect the response of both normal tissues and tumors to a course of radiation.
Using daily fractionation with time intervals of approximately 24 hours between fractions, there is adequate time for repair to occur. If the radiotherapy factions are too close together (i.e., less than 6 hours) then, unrepaired damage will accumulate. Although this may be beneficial for tumor cell killing, it can result in substantial normal-tissue damage and increase the rate of treatment-related complication, thereby reducing the potential therapeutic ratio.
Using daily fractionation with time intervals of approximately 24 hours between fractions, there is adequate time for repair to occur. If the radiotherapy factions are too close together (i.e., less than 6 hours) then, unrepaired damage will accumulate. Although this may be beneficial for tumor cell killing, it can result in substantial normal-tissue damage and increase the rate of treatment-related complication, thereby reducing the potential therapeutic ratio.
 FIGURE 41.3 The target cell hypothesis and the rationale for low dose per fraction. The cell survival curve for late-responding tissues is more curved than that for tumors or early-responding tissues as shown in Figure 41.2. When radiation dose is fractionated, and provided that the interfraction interval is sufficiently long, the shoulder portion of the respective curves is repeated, following each fraction. Fractionation will tend to spare late-responding tissues such as spinal cord, heart, and kidney relative to the tumor or early-responding tissues such as skin or gastrointestinal cells. With increasing number of fractions, there is greater kill of tumor cells—with a possible added effect from redistribution and reoxygenation—but with a potential benefit being reduced by accelerated repopulation is the overall treatment time is extended. Late-responding tissues are less affected by the overall treatment time but are relatively more sensitive to fraction size, as reflected by their lower α / β ratio. Thus, if large dose per fraction is used, then the total dose needs to be reduced in order to maintain the same level of normal-tissue toxicity. |
TABLE 41.1 The Four R’s of Radiotherapy | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
|
Redistribution A general schema divides the biological cell cycle into four phases: (a) mitosis, or M phase; (b) G1 phase; (c) DNA synthesis, or the S phase; and (d) G2 phase. Cells in the late G2 and M phase of the cell cycle tend to be most sensitive to irradiation, whereas those in the mid-late S and early G2 phase are more radioresistant.18 This means that after irradiating a population of proliferating cells, surviving cells will predominantly be in the radioresistant late S and early G2 phases. During a course of fractionated radiotherapy, these surviving cells will progress through the cell cycle and “redistribute” into more radiosensitive phases in the interval between fractions and will be “caught” in a relatively more sensitive phase by the next fraction of radiation.
Radiation blocks cell progression through the cell cycle at the G2-M and the G1-S checkpoints. These checkpoints are controlled by several genes. The radiation induced G1 block is p53 dependent,19 but as many tumors are p53 deficient, the G2 block may be more important in tumors receiving radiation. The duration of the G2 block is dose dependent.20,21
Repopulation Cells in both normal tissues and tumors may respond to a cytotoxic insult by accelerated repopulation.22,23 Early-reacting tissues, such as the gastrointestinal mucosa, have a high cellular repopulation capacity, and this is an important component of their response to chemotherapy and radiation therapy. A reduction in overall treatment time will reduce the time available for repopulation in these tissues and lead to more side effects. Late-reacting tissues proliferate slowly and show less of a proliferative response to cytotoxic therapy, thus changing the treatment intensity is less important for these tissues. Accelerated repopulation, as reflected by the overall time factor, has been demonstrated in many cancers. Most convincingly, this has been shown by the outcome of a large number of randomized controlled trials of intensified radiation therapy for squamous cell carcinoma of the head and neck.24 In head and neck squamous cell carcinoma (HNSCC), there are relatively reliable estimates of the dose recovered (or lost) per day because of proliferation, and this is consistently estimated at around 0.6 Gy/day.25 This represents the increased total dose required to compensate for tumor repopulation, resulting from a 1-day protraction of treatment. This implies that if 2 Gy/day was used, the effective dose would only be 1.4 Gy as 0.6 Gy would be lost to counteract the effect of tumor repopulation. The lag time before repopulation takes effect will vary between different tissues and tumors and likely between patients. This lag time period may be in the region of 2 to 3 weeks24 for HNSCC.
Reoxygenation Human tumors often contain hypoxic regions, and it was hypothesized as early as the 1950s26 that this may be associated with radiation resistance. Hypoxic radioresistance has been documented and extensively studied in cells in vitro as well as in small animal tumor models. Oxygen is thought to inhibit the cellular repair of DNA damage induced by free radicals thereby “fixing” the radiation damage. More recently, it has been shown that hypoxic tumors also have a poorer outcome after chemotherapy or surgery, and a link has been established between malignant progression and hypoxia. 27 Research has shown that tumor cells under hypoxic conditions switch on several survival pathways that let them survive in a hypoxic microenvironment and confer resistance against cytotoxic therapy. Reoxygenation refers to the process by which previously hypoxic cells become better supplied by oxygen as they are brought closer to well-perfused regions when tumor cells in these oxygenated areas die during a course of radiation.
The fact that tumor oxygenation assessed at baseline (i.e., before the start of any therapy, by means of polarographic), microelectrodes is associated with survival after fractionated
radiotherapy in HNSCC proves that reoxygenation cannot completely offset the detrimental effect of hypoxia.28 Whether this is because reoxygenation is not 100% efficient in countering radiobiological hypoxia or a result of the link between hypoxia and malignant, progression remains to be clarified.
radiotherapy in HNSCC proves that reoxygenation cannot completely offset the detrimental effect of hypoxia.28 Whether this is because reoxygenation is not 100% efficient in countering radiobiological hypoxia or a result of the link between hypoxia and malignant, progression remains to be clarified.
HYPERFRACTIONATED AND ACCELERATED RADIOTHERAPY
Cancer radiotherapy was widely introduced in clinical practice in the early 20th century, and it soon became apparent that the way radiotherapy was delivered over time had a major influence on tumor and normal-tissue effects. Indeed, as discussed earlier in this chapter, fractionated radiotherapy was introduced as a method to take advantage of the differential in the four R’s between (most) tumor histologies and dose-limiting normal tissues. Even in those early days, the overall treatment time (i.e., the time elapsed between the first and the last day of radiotherapy), was recognized as a factor determining side effects.
Most of the altered radiotherapy fractionation schedules have explored two types of modification: hyperfractionation (HFX) and accelerated fractionation (AF). There is no consensus as to the definition of these two concepts, and some authors have proposed definitions based on a more or less complicated link between the time-dose factors of a fractionated regime of radiotherapy, namely the dose per fraction, number of fractions, daily or weekly dose, overall treatment time, and total dose. This has led to some confusion regarding the classification of radiotherapy schedules, and there is a need to return to more general definitions, directly reflecting the different rationales underpinning nonconventional schedules.29 Indeed, the concept of HFX is essentially linked to dose fraction size and not to time. Therefore, any schedule employing a dose per fraction of less than 1.8 Gy is classified as hyperfractionated. AF relates to the intensity of therapy over time and, therefore, a schedule in which the rate of dose accumulation exceeds 10 Gy/wk is classified as accelerated. This simple definition, besides its pedagogic character, has the advantage of being applicable to all altered fractionation schedules. In addition, it clearly separates the issues of dose/fraction from overall treatment time and total dose, which result from distinct radiobiological concepts. In a schedule using a dose per fraction different from 2 Gy, the rate of dose accumulation is estimated from the total dose converted into the biologically equivalent dose in 2-Gy fractions (EQD2) using the linear-quadratic model with an assumed α / β of 10 Gy for non-small cell lung cancer (NSCLC). Similarly, a schedule employing a dose per fraction exceeding 2.2 Gy is classified as hypofractionated.
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
