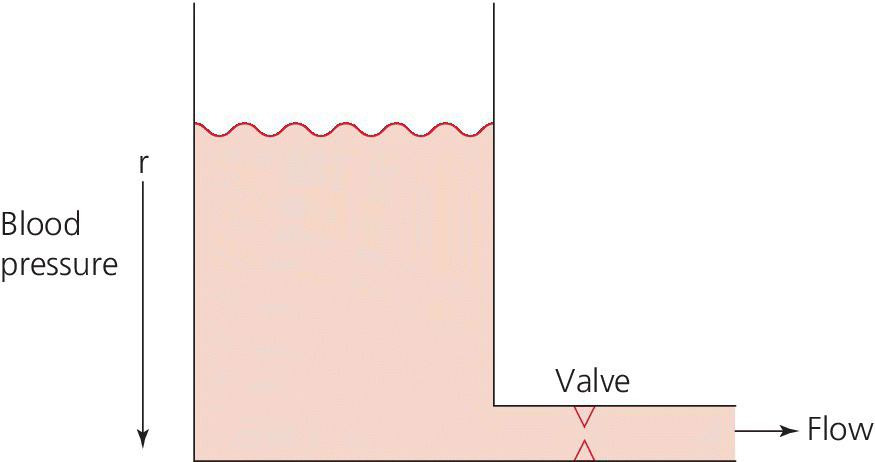
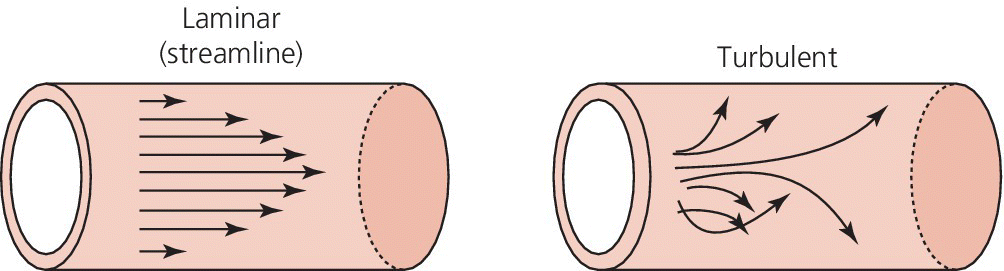
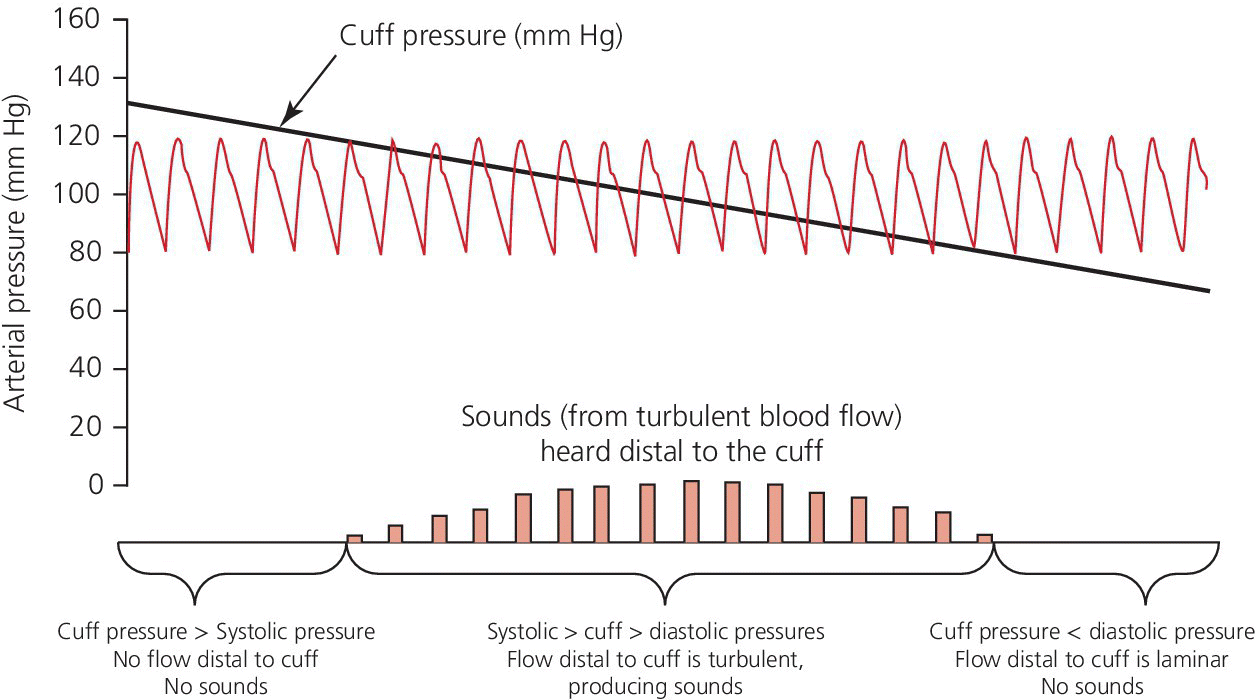
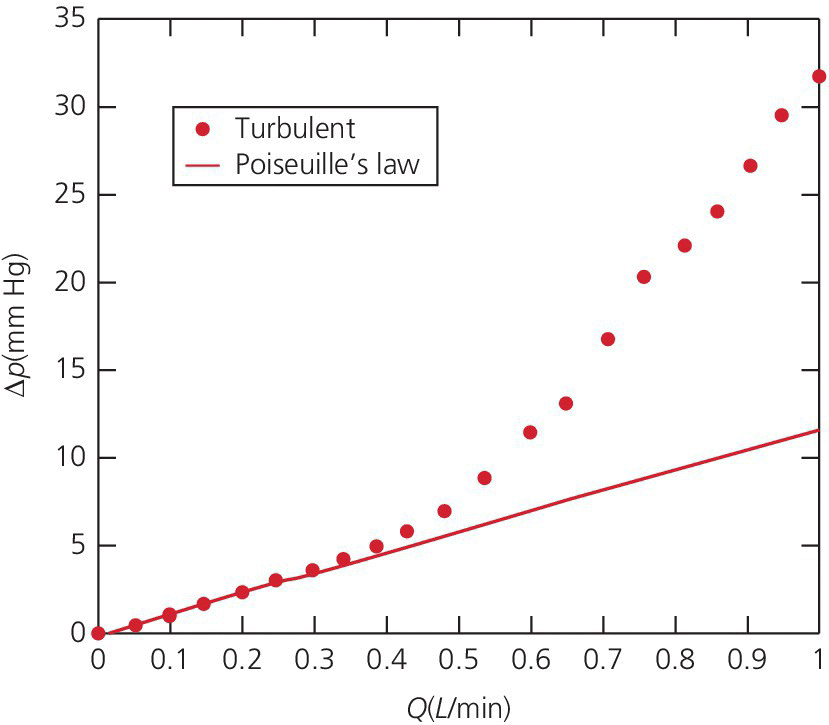
CHAPTER 1 James E. Faber and George A. Stouffer Hemodynamics is concerned with the mechanical and physiologic properties controlling blood pressure and flow through the body. A full discussion of hemodynamic principles is beyond the scope of this book. In this chapter, we present an overview of basic principles that are helpful in understanding hemodynamics. Daniel Bernoulli was a physician and mathematician who lived in the eighteenth century. He had wide‐ranging scientific interests and won the Grand Prize of the Paris Academy 10 times for advances in areas ranging from astronomy to physics. One of his insights was that the energy of an ideal fluid (a hypothetical concept referring to a fluid that is not subject to viscous or frictional energy losses) in a straight tube can exist in three interchangeable forms: perpendicular pressure (force exerted on the walls of the tube perpendicular to flow; a form of potential energy), kinetic energy of the flowing fluid, and pressure due to gravitational forces. Perpendicular pressure is transferred to the blood and vessel wall by cardiac pump function and vascular elasticity and is a function of cardiac output and vascular resistance. where V is velocity and ρ is density of blood (approximately 1060 kg/m3) where g is gravitational constant and h is height of fluid above the point of interest. Although blood is not an “ideal fluid” (in the Newtonian sense), Bernoulli’s insight is helpful. Blood pressure is the summation of three components: lateral pressure, gravitational forces, and kinetic energy (also known as the impact pressure or the pressure required to cause flow to stop). Pressure is the force applied per unit area of a surface. In blood vessels or in the heart, the transmural pressure (i.e., pressure across the vessel wall or ventricular chamber wall) is equal to the intravascular pressure minus the pressure outside the vessel. The intravascular pressure is responsible for transmural pressure (i.e., vessel distention) and for longitudinal transport of blood through the vessels. Gravitational forces are important in a standing person. Arterial pressure in the foot will exceed thoracic aortic pressure due to gravitational pull on a column of blood. Likewise, arterial pressure in the head will be less than thoracic aortic pressure. Similarly, gravitational forces are important in the venous system, since blood will pool in the legs when an individual is standing. Decreased ventricular filling pressure results in a lower cardiac output and explains why a person will feel lightheaded if rising abruptly from a sitting or supine position. In contrast, gravity has negligible effect on arterial or venous pressure when a person is lying flat. Gravitational pressure equals the height of a column of blood × the gravitational constant × the fluid density. To calculate hydrostatic pressure at the bedside (in mm Hg), measure the distance in millimeters between the points of interest, for example heart and foot, and divide by 13 (mercury is 13 times denser than water). Kinetic energy is greatest in the ascending aorta where velocity is highest, but even there it contributes less than 5 mm Hg of equivalent pressure. One of the properties of a fluid (or gas) is that it will flow from a region of higher pressure (e.g., the left ventricle) toward a region of lower pressure (e.g., the right atrium; Figure 1.1). In clinical practice, the patient is assumed to be supine (negating the gravitational component of pressure) and at rest. As already mentioned, kinetic energy is negligible compared to blood pressure at normal cardiac output and thus blood flow is estimated using the pressure gradient and resistance. Figure 1.1 A simple hydraulic system demonstrating fluid flow from a high‐pressure reservoir to a low‐pressure reservoir. Note that the volume of flow can be affected by a focal resistance (i.e., the valve). The primary parameter used in clinical medicine to describe blood flow through the systemic circulation is cardiac output, which is the total volume of blood pumped by the ventricle per minute (generally expressed in L/min). Cardiac output is equal to the total volume of blood ejected into the aorta from the left ventricle (LV) per cardiac cycle (i.e., stroke volume) multiplied by the heart rate. This formula is important experimentally, but of limited used clinically because stroke volume is difficult to measure. Cardiac output is generally measured using the Fick equation or via thermodilution techniques, which are discussed in Chapter 6. To compare cardiac output among individuals of different sizes, the cardiac index (cardiac output divided by body surface area) is used. Normalization of cardiac output for body surface area is important, as it enables proper interpretation of data independent of the patient’s size (e.g., cardiac output will obviously differ widely between a 260‐pound man and a 100‐pound woman). Indexing to body surface area is also used for other measurements such as aortic valve area. The relationship between blood flow, resistance, and pressure can be determined using a modification of Ohm’s law for the flow of electrons in an electrical circuit: where ΔP is the difference in pressure between proximal and distal points in the system and R is the hydraulic resistance to blood flow between the proximal and distal points. A useful clinical equation based on Ohm’s law is: Using this equation, we can calculate systemic vascular resistance knowing cardiac output, CVP, and arterial pressure. MAP is the average arterial pressure over time and is generally estimated using the following formula: This formula was developed for a heart rate of 60 beats per minute (bpm; at this heart rate, diastole is twice as long as systole) and becomes progressively more inaccurate as heart rate increases. In a patient in shock (i.e., low blood pressure and impaired tissue perfusion), measurement of CO and calculation of SVR can help identify the etiology (e.g., septic shock with high CO + low SVR or cardiogenic shock with low CO + high SVR). Blood is not an “ideal fluid” and energy (and pressure) is lost as flowing blood encounters resistance to flow. Resistance to blood flow is a function of viscosity, vessel radius, and vessel length in a vessel without any focal obstruction (resistance to blood flow also occurs from focal obstruction such as seen with atherosclerotic disease of arteries). The relationship is known as Poiseuille’s law (sometimes referred to as the Poiseuille–Hagen law) and is described by the following equation: or, since flow = difference in pressure/resistance: Since radius is raised to the fourth power, its importance in determining resistance is paramount. A 20% increase in radius leads to a doubling in flow if all other variables are constant. Or, as another example, resistance is 16 times greater in a coronary artery with a diameter of 2 mm (e.g., a distal obtuse marginal) than in a coronary artery with a diameter of 4 mm (e.g., the proximal left anterior descending). Viscosity is also important in determining resistance (commonly abbreviated as η and with units of poise = dyne s/cm2). It is difficult to measure directly and thus is commonly reported as relative to water. The viscosity of plasma is 1.7 × viscosity of water and viscosity of blood is 3–4 × viscosity of water, the difference being due to red blood cells and thus hematocrit. It is important to note that Poiseuille’s law only provides an approximation of resistance when used in blood vessels. The four important assumptions underlying the derivation of this equation are: (1) the viscosity of the fluid is unchanging over time or space; (2) the tube is rigid and cylindrical; (3) length of the tube greatly exceeds diameter; and (4) flow is steady, nonpulsatile, and nonturbulent. Many of these assumptions are violated when this equation is applied to blood flow in the body. Poiseuille’s law is important, however, as it indicates the variables that are the determinants of resistance to flow. In the mammalian circulation, resistance is greatest at the level of the arterioles. While the radius of a typical capillary (e.g., 2.5 microns) is smaller than the radius of the smallest arterioles (e.g., 4 microns), the number of capillaries greatly exceeds the number of arterioles, and thus the effective area is much larger. Also of importance is that arteriolar resistance can be regulated (capillaries have no smooth muscle and thus resistance cannot be regulated at that level; however, pericyte cells can constrict capillaries in certain specialized structures like the kidney’s glomerulus). This enables rapid changes in vascular resistance to maintain blood pressure (e.g. in hypovolemic shock) and also enables regulation of blood flow to various organs (i.e., autoregulation). A general principle to remember is that reduction of arteriolar resistance in a tissue decreases SVR, resulting in increased cardiac output while simultaneously decreasing pressure proximal to the arterioles and increasing pressure distal to the arterioles. Flow in blood vessels, as in any hydraulic system, is usually smooth and orderly because the fluid separates into an infinite number of concentric layers, with the highest velocity in the center and the lowest next to the vessel wall. When a fluid (such as blood) flows past a solid surface (such as the vascular wall), a thin layer develops adjacent to the surface where frictional forces retard the motion of the fluid (Figure 1.2). There is a gradient of frictional resistance (and thus velocity) between fluid in contact with the solid surface and fluid in the center of the stream. If the fluid elements travel along well‐ordered, nonintersecting layers, this is termed laminar flow. The flow resistance in laminar flow is due entirely to viscous resistance of the fluid and the interactions between the fluid and the stationary wall. In laminar flow, the average velocity of a fluid is one half of the maximum velocity observed in the center of the stream. Figure 1.2 Schematic of laminar flow. Flow in straight, nonbranching tubes is usually smooth and orderly because the fluid separates into an infinite number of concentric layers with different velocities. When a fluid (such as blood) flows past a stationary surface (such as the vascular wall), a thin layer develops adjacent to the surface where frictional forces tend to retard the motion of the fluid. There is a gradient of frictional resistance (and thus velocity) between fluid in contact with the solid surface and fluid in the center of the stream. If the fluid particles travel along well‐ordered, nonintersecting layers, this is termed laminar flow. In contrast, turbulent flow occurs when fluid elements from adjacent layers become mixed. Turbulent flow is chaotic and less efficient because of energy losses (these losses are termed inertial resistance). In turbulent flow, the relationship between pressure difference and flow is no longer linear, since the amount of resistance in the tube increases with flow. Thus, larger pressure differences are required to maintain flow. Turbulence, and associated loss of energy along with the narrowed radius, are two of the primary causes of the drop in pressure that occurs distal to a severe stenosis. Turbulence is important for several reasons, one of which is that it creates noise (e.g., in a pipe when flow velocity is high), which is the cause of some cardiac murmurs and the Korotkoff sounds (used when measuring blood pressure; Figure 1.3). Another is that turbulence alters the relationship between flow and perfusion pressure, as already mentioned. Because of increased energy losses associated with turbulence, the relationship between perfusion pressure and blood flow is no longer linear (as described by the Poiseuille relationship) but rather, greater pressure is required to maintain adequate flow (Figure 1.4). Figure 1.3 Schematic illustrating the use of transient transition from laminar to turbulent flow in measuring blood pressure. Figure 1.4 Transition from laminar to turbulent flow. Note that the pressure gradient required to increase flow increases markedly when flow transitions from laminar to turbulent. The transition from laminar to turbulent flow can be predicted by calculating the Reynold’s number, which is the ratio of inertial forces (Vη) to viscous forces (ρ/L):
Introduction to basic hemodynamic principles
1. Energy in the blood stream exists in three interchangeable forms: pressure arising from cardiac output and vascular resistance, “hydrostatic” pressure from gravitational forces, and kinetic energy of blood flow
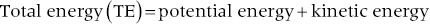
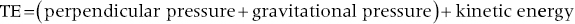
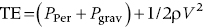
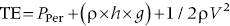
2. Blood flow is a function of pressure gradient and resistance
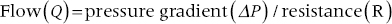
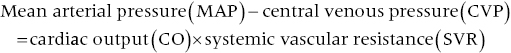
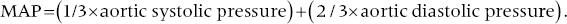
3. Resistance to flow can be estimated using Poiseuille’s law
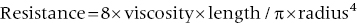
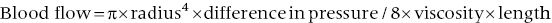
4. Reynold’s number can be used to determine whether flow is laminar or turbulent
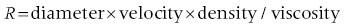
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


