The Heart as a Muscular Pump
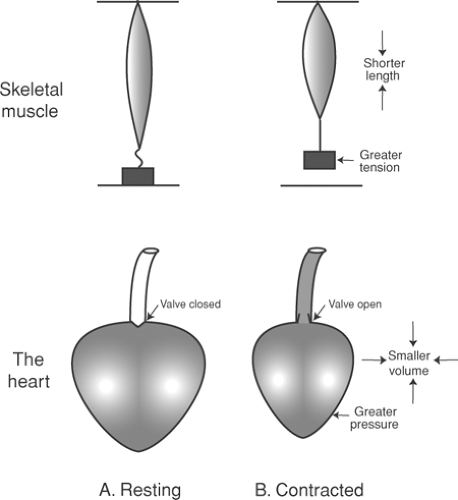
Unlike the contraction of a skeletal muscle, which is characterized by changes in tension and length, the beating heart generates pressure and ejects a volume of blood. For this reason, when describing the work of this hollow muscular structure, changes in length and tension must be redefined as changes in volume and pressure (Fig. 11-1).
Fiber Length and Chamber Volume: A Geometric Relationship
The relationship between length and volume is determined by the laws of geometry. In a sphere, for example, volume is defined by the equation:
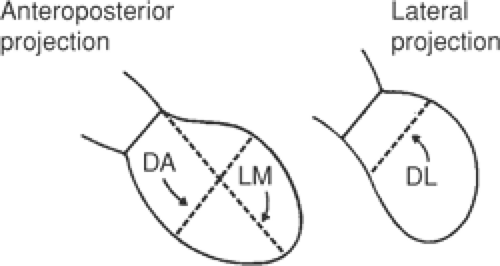
where V = volume and R = radius. Volume is also related to the third power of circumference, so that doubling circumference increases volume eightfold (23). Although the left ventricle is not a sphere, its shape can be approximated as an ellipsoid with three diameters: anterior-posterior diameter (DA), lateral diameter (DL), and maximal length (LM) (Fig. 11-2). These can be used to estimate left ventricular volume according to the following equation that describes the volume of an ellipse:
Wall Stress and Chamber Pressure: The Law of Laplace
The pressure developed within a chamber of the beating heart is determ ined by the stress within the chamber walls, the volume of the chamber, and wall thickness. Although the terms tension and stress are sometimes used interchangeably, this is incorrect; tension describes a force exerted along a line (e.g., dynes/cm), whereas stress is a force exerted across an area (e.g., dynes/cm2). The pressure within the chamber, like the stress developed by the chamber walls, has the units dynes/cm2 because it is a force exerted across an area. The difference is that wall stress is a force that parallels the circumference of the walls, whereas pressure is a distending force that is exerted at right angles to the walls. Pressures are usually described as millimeters of mercury (mm Hg) or centimeters of water (cm H2O); these are the gravitational forces exerted by a column of mercury or water of the stated height. When converted to centimeter-gram-second (cgs) units, 1 mm Hg = 1330 dyn/cm2 and 1 cm H2O = 980 dyn/cm2.
 Fig. 11-1: Comparison of a skeletal muscle (A), which shortens and develops tension (above), and the heart (B), whose contraction reduces chamber volume and increases pressure (below). In the resting skeletal muscle, the load rests on a support; in the resting heart, the load (arterial pressure) is separated from the ventricle by a semilunar valve. |
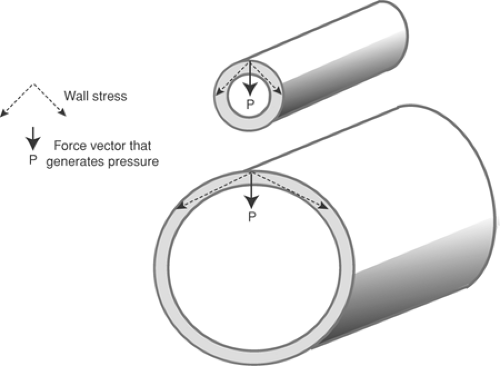
The relationships between the pressure within a chamber, wall stress, chamber size, and wall thickness are described by the law of Laplace. In its simplest form, which describes a cylinder with infinitely thin walls (Fig. 11-3), the law of Laplace states that wall tension is equal to the pressure within the cylinder times its radius:
where T is wall tension (dynes/cm), P is pressure (dynes/cm2), and R is radius (cm). An important corollary of the law of Laplace is that when the pressure within the thin-walled cylinder is held constant, the tension on its walls increases with increasing radius, and vice versa.
The law of Laplace is more complex in a thick-walled chamber, where wall stress (θ) is inversely proportional to wall thickness (h). This is easily understood because when wall thickness is increased, the stress across any area within the wall decreases. The law of Laplace, as applied to a thick-walled cylinder, is therefore:
 Fig. 11-2: Outline of the chamber of the left ventricle viewed in anteroposterior and lateral projections. Volume can be estimated by assuming the chamber to be an ellipse whose long axis is LM, and whose short axes are DA and DL. |
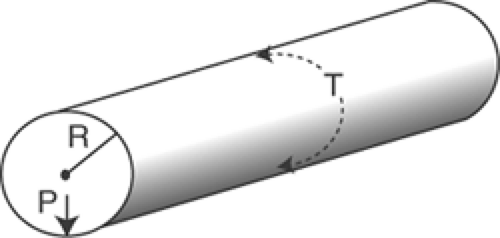 Fig. 11-3: The law of Laplace in a thin-walled cylinder relates wall tension (T) to the pressure within the cylinder (P) and the radius of curvature (R). |
A greater wall stress is required to achieve a given pressure in a larger chamber because, when the diameter increases, a smaller proportion of the force developed by the chamber walls is directed toward the center of the chamber (Fig. 11-4).
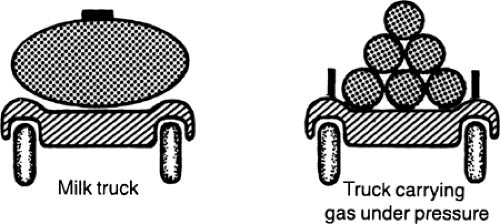
A familiar application of the law of Laplace is seen in the trucks used to transport fluids and gases in which, to minimize the hazard of bursting, the tanks that carry compressed gasses at high internal pressures are constructed with smaller radii than tanks that carry liquids at low pressures (Fig. 11-5). The tendency of a tank to burst can also be reduced by increasing the thickness of its walls simply because the greater wall thickness reduces the stress on each element in the wall.
The complex geometry of the ventricles makes it impossible to calculate wall stress with precision, but the law of Laplace states that dilation increases the tension that must be developed by the muscle fibers in the walls of the heart to generate a given chamber pressure, and that at any given chamber pressure, increasing wall thickness (hypertrophy) reduces the amount of tension on each muscle fiber. Dilatation of the heart is deleterious because, by increasing wall stress at any chamber pressure, more work must be done during systole to stretch elastic and viscous elements in
the walls of the heart. Conversely, the smaller decrease in wall stress during ejection by a dilated heart reduces its ability to use energy stored in the stretched elasticities to perform external work (see Chapter 12).
the walls of the heart. Conversely, the smaller decrease in wall stress during ejection by a dilated heart reduces its ability to use energy stored in the stretched elasticities to perform external work (see Chapter 12).
 Fig. 11-4: The law of Laplace in a thick-walled cylinder. The wall stress () needed to achieve a given pressure () is greater in the larger cylinder because a smaller proportion of the force developed in the walls is directed toward the center of the cylinder. |
 Fig. 11-5: A practical application of the law of Laplace. A single tank with a large radius of curvature is used in a milk truck, where the pressure in the tank is low (left). Trucks used to transport gas under high pressure contain several cylindrical tanks, each with a short radius of curvature (right). |
Distribution of Stress across the Walls of the Heart
Stress is not distributed uniformly throughout the layers of the ventricular walls, but instead is greatest in the inner (endocardial) regions (Mirsky, 1969; Fenton et al., 1978). This might appear to contradict the law of Laplace, which states that wall stress increases as chamber diameter increases, but there is no contradiction because the distribution of stress among the layers of a thick-walled ventricle is not the same as the average amount of stress in the walls of ventricles that have different chamber sizes. The differences in wall stress in the various layers of the ventricle can be understood by viewing the ventricle as a series of concentric elastic spheres, where an increase in chamber volume causes the greatest increase in stress in the innermost layer. These differences are magnified when wall thickness increases, so that a marked increase in the pressure developed by a thick-walled hypertrophied heart can cause severe energy starvation, and even necrosis, of the subendocardium. Compression of the muscular branches of the coronary arteries that penetrate the ventricular wall from their origins in epicardial coronary arteries (see Chapter 1) also increases the vulnerability of the inner layers of the ventricular wall to energy starvation.
Cycles of Contraction and Relaxation: Pressure-Volume Loops
Table 11-1 lists five major determinants of cardiac performance, of which three are properties of the heart and two are governed by the circulation. Among the former, heart rate is normally determined by pacemaker currents in the SA node (see Chapter 13), and inotropy and lusitropy by the biochemical and biophysical properties of the working cardiac myocytes (see Chapter 10). The key circulatory determinants of cardiac performance are venous return, which along with lusitropic properties determines preload, and aortic pressure, which along with inotropy determines afterload.
Pressure-volume loops, which describe changes in ventricular pressure as a function of chamber volume, provide a valuable way to analyze the hemodynamic abnormalities in cardiovascular disease. To understand these diagrams, it is useful first to consider a preloaded skeletal muscle that lifts a heavy afterload (Fig. 11-6). As detailed in Chapter 3, a preload is a small load supported by a muscle before it is stimulated to contract, while an afterload is a heavier load that is lifted after contraction begins, when the tension developed by the muscle exceeds the weight of the afterload.
Table 11-1 Major Determinants of the Work of the Heart | |||||||
|---|---|---|---|---|---|---|---|
|
Skeletal Muscle
The cycle of contraction and relaxation depicted in Figure 11-6 can be divided into four phases; two of contraction and two of relaxation. The first phase, isometric contraction (A in Fig. 11-6), begins when the activated muscle starts to develop tension; however, as long as muscle tension is less than the afterload, shortening cannot occur. The second phase, isotonic contraction (B in
Fig. 11-6), begins when active tension equals the afterload, after which the muscle begins to lift the afterload. Shortening then continues at a constant tension, which is equal to the weight of the afterload (the small preload is ignored). The third phase, isotonic relaxation (C in Fig. 11-6), begins when the relaxing muscle starts to lengthen while still bearing the afterload. Lengthening continues at the constant tension of the afterload until the latter returns to the support and so is removed from the muscle. This marks the beginning of the fourth phase, isometric relaxation (D in Fig. 11-6), during which tension is dissipated in the unloaded muscle. These four phases can be plotted as a “work diagram” (Fig. 11-7), which shows how tension and length change during the contraction shown in Figure 11-6. Because the muscle shortens and lengthens with the same afterload, the curves for isotonic contraction and isotonic relaxation in Figure 11-7 are superimposed.
Fig. 11-6), begins when active tension equals the afterload, after which the muscle begins to lift the afterload. Shortening then continues at a constant tension, which is equal to the weight of the afterload (the small preload is ignored). The third phase, isotonic relaxation (C in Fig. 11-6), begins when the relaxing muscle starts to lengthen while still bearing the afterload. Lengthening continues at the constant tension of the afterload until the latter returns to the support and so is removed from the muscle. This marks the beginning of the fourth phase, isometric relaxation (D in Fig. 11-6), during which tension is dissipated in the unloaded muscle. These four phases can be plotted as a “work diagram” (Fig. 11-7), which shows how tension and length change during the contraction shown in Figure 11-6. Because the muscle shortens and lengthens with the same afterload, the curves for isotonic contraction and isotonic relaxation in Figure 11-7 are superimposed.
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
