Oral direct thrombin inhibitors (DTIs) have been postulated to increase the risk of myocardial infarction (MI). The meta-analysis by Artang et al has exhaustively explored this topic by addressing 2 separate questions: (1) Is there an excess rate of MI that can be attributed to DTIs? (2) Does warfarin reduce the incidence of MI to a greater extent than nonwarfarin anticoagulants? Based on 2 separate data sets of randomized controlled trials, Artang et al have interpreted their findings by concluding that DTIs are associated with an increased risk of MI and that warfarin does not differ from the other anticoagulants in the risk of MI.
We have carried out a trial sequential analysis (TSA) to reexamine the same 2 data sets published by Artang and coworkers. Based on our results, our conclusions are quite different from those of these investigators because (1) the increased risk of MI from DTIs does not seem to be conclusively demonstrated and (2) the similar rates of MI observed between warfarin and nonwarfarin anticoagulants not only indicate no proof of difference but also demonstrate the proof of no difference.
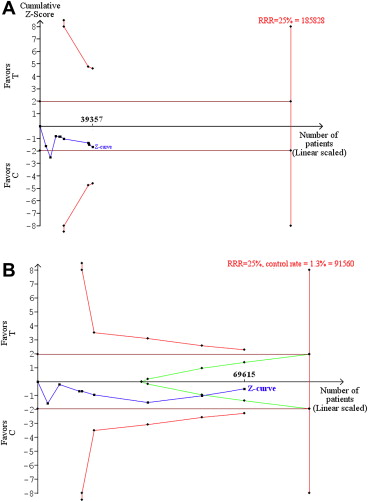
From a methodologic point of view, TSA is known to appropriately address the quite frequent case of meta-analyses showing borderline results. One feature of TSA is that its methodology requires to declare a prespecified incremental benefit; another important feature of TSA is that an estimate is generated of the optimal information size, that is, an estimate of the ideal cumulative number of patients required to draw a firm conclusion on the therapeutic problem under examination. The assumptions of our TSA included 2-sided testing, type I error = 5%, and power = 80%. With respect to the end point of MI, the intervention effect was set at a relative risk reduction of 25%. The expected absolute event rate was equal to the cumulative arithmetic rate in the control groups of the 2 data sets (i.e., 0.8% and 1.3% in the 2 TSAs, respectively). The main result of our TSAs was expressed through the graph of cumulative z curve; the boundaries in this graph for concluding superiority, inferiority, or futility were determined according to the O’Brien-Fleming alpha spending function. All calculations were carried out using a specific statistical software (TSA, User Manual for TSA; Copenhagen Trial Unit 2011, Copenhagen, Denmark, software downloadable at www.ctu.dk/tsa ).
Figure 1 summarizes the results of our 2 TSAs. In the first data set, although the z curve confirmed the hypothesis that the risk of MI might be increased with DTIs, this hypothesis remained quite far from a conclusive demonstration; in fact, the z curve remained far from the boundaries of inferiority and, more importantly, the optimal information size was estimated at 185,828 patients, which is much more than the cumulative number of patients studied thus far (n = 39,357). Hence, many more data are needed to settle this question. In the second data set, the z curve clearly demonstrated the proof of no difference; interestingly enough, the findings from this second TSA were conclusive because although the available patients (n = 69,615) were fewer than the optimal information size (n = 91,560), the last point of the z curve was clearly within the boundaries of futility; so, there is no need to collect more data to settle this specific therapeutic question.