3

This chapter provides human morphometric data that give insight into structure-functional correlations in the lung, and some appropriate information is also given about commonly used laboratory animals. It is not the purpose of this chapter to provide a comprehensive review of morphometry, but instead to give a very brief account of techniques as they apply to the lung, written as simply as possible. The reader is referred to classical studies and comprehensive reviews on the subject1–8 and Weibel’s⁹ classic monograph on the morphometry of the human lung.

Morphometric Techniques and Their Application to the Lung

Morphometry is the term applied to measurement of form or structure. The term stereology is often used synonymously, but it actually means the study of three-dimensional properties of objects usually projected to a plane. Stereology carries with it the observation that what one sees down the microscope may be illusory and not truly representative of what exists in three dimensions. As a simple example, consider a sphere and a cylinder that have the same volume. There will thus be the same numbers of spheres as cylinders in the same volume. Arbitrarily, let the height of the cylinder be 10 times its radius. By simple arithmetic, the radius of the cylinder is 0.5109 the radius of the sphere, and its height is 5.109 times the radius of the sphere. The mean intercept area (the average transectional area) of this sphere is 2/3φr² and that of the cylinder is 2φr²h/φr + h. By simple arithmetic again, the mean intercept area of the sphere is 1.68 times as large as that of the cylinder. For the cylinders to be equal to the same area on cross section, there will have to be many more cylinders. In other words, a cylinder appears to be 1.68 times more frequent on a cross section than the truly equal number in three dimensions. Similarly, a change in linear dimension is cubed in three dimensions and thus a 26% linear increase results in an increase of 100% in volume.

Commonly Used Equations

Three simple morphometric equations are often used:

1. Volume densities (proportions):

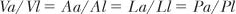
where Va, Aa, La, and Pa are volume, area, length, or points, respectively, of component a, and Vl, Al, Ll, and Pl are the volume, area, length, and points of the lung, l. In other words the area, length, or points that lie over a component a divided by the total area, length, or points over the lung are proportional to each other and to the volume that a forms of lung volume. These are referred to as the volume densities or volume proportions. This technique may provide volume densities of such normal structures as alveoli, airways, or vessels, or, in the case of disease, of emphysema.

As an example, the results of five different studies^10–14 that have measured volume densities of lung structure in 7- or 8-week-old Sprague-Dawley rats are shown in Table 3–1. The standard errors of these volume densities are small. Alveolar wall forms 15% of lung volume; this figure is too high because the ratio of lung volume to lung weight is ~10 in this species. The high-volume density of alveolar walls occurs because of section thickness, which exaggerates volume proportions of tissues whose size approximates section thickness (see Holmes effect, discussed later).

Vv, volume density.

Date from Kida K, Thurlbeck WM. Lack of recovery of lung structure and function after the administration of beta-aminopropionitrile in the postnatal period. Am Rev Respir Dis 1980;122:467–475; Kida K, Utsuyama M, Takizawa T, Thurl-beck WM. Changes in lung: morphologic features and elasticity caused by streptozotocin-induced diabetes mellitus in growing rats. Am Rev Respir Dis 1983;128:125–131; Kida K, Yasui S, Utsuyama M, Ofulue AF, Thurlbeck WM. Lung changes resulting from intraperitoneal injections of porcine pancreatic elastase in suckling rats. Am Rev Respir Dis 1984;130:1111–1117; Ofulue AF, Kida K, Thurlbeck WM. Experimental diabetes and the lung. I. Changes in growth morphometry and biochemistry. Am Rev Respir Dis 1988;137:162–166; and Kida K, Thurlbeck WM. Tracheal banding in weanling rats diminishes lung growth and alters lung architecture. Pediatr Res 1981;15:269–277.

2. Surface area, most commonly of the gas exchanging tissue:

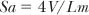
where Sa is the surface area, V is the volume of the lung in which Lm is measured, and Lm is the length of a test line placed over the lung, usually using light microscopy of histologic sections, divided by the number of alveolar intercepts, counted as 1 through an alveolar wall, as opposed to through an alveolar surface.¹⁵ (A point of confusion may arise when actually performing the counts; as it is difficult to count in halves, most people count 2 when the line passes through a wall, and 1 when it enters into or touches the wall; this difference in counting can be compensated mathematically by using the equation Lm = 2l/i, where l represents the length of the test line and i represents the number of counts.) This formula was devised by Dunnill.⁸

However, surface area is more commonly expressed as 2Vi/l, where l is the length of the test line divided by the alveolar surface intercepts (i), and this equation applies to space-filling contiguous particles, such as alveoli in the lung. If this formula is utilized, Lm is the distance between alveolar surfaces.

Lm is widely used as a measurement of airspace size, which it approximates, but is often ambiguously described. The interalveolar wall distance is an easier concept to grasp than interalveolar surface distance. Interalveolar wall distance reflects the size of alveolar ducts and sacs as well as alveoli, and is affected by the lung tissue in which it is measured. Interalveolar surface distance represents both the interalveolar wall distance and the distance between surfaces of the alveolar wall.¹⁵ The true mean cord length or mean cord intercept of alveoli and alveolar ducts can easily be obtained from simple morphometry.¹⁶ A more precise measurement of airspace size is the airspace wall surface to volume ratio (Sv), which is reciprocally related to Lm.¹⁷ Accurate prediction data are available for lungs of nonsmokers.¹⁸

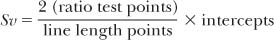
Alveolar surface area has often been measured in the human, and a large variation (40 to 100 m²) was found in one study.¹⁸ The variation was stature dependent (which affects lung volumes). Lm was stature independent but increased with age.

3. Number of alveoli per unit volume:

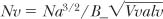
where Nv is the number of alveoli per unit volume, Na is the number per unit area, B is a shape constant related to the average volume of an alveolus to its average surface area, and Vvalv is the volume density of alveoli.

This equation was developed by Weibel and Gomez,³ but for several reasons has lost popularity among those interested in morphometry. The equation applies to one alveolus, and its accurate use requires that the average alveolar dimensions be normally distributed. The evidence is that this is true in normal adult lungs.⁹ The shape constant of the human alveolus is unknown, and a value of 1.55 is commonly used. The exact shape of a human alveolus is not known with certainty, but those of models often used for alveoli (for example a ⅚ sphere or an open-faced dodecahedron) are closely similar. However, the most serious criticism is that alveoli are not easily distinguished from alveolar ducts and sacs on single histologic sections.¹⁹ This problem may not be as difficult as it is made out to be, provided that alveolar ducts and sacs are defined as the “core” of air internal to alveoli in alveolar ducts and sacs.²⁰

In any event, it has been widely used in the past in human and animal lungs. In human lungs, there is a large variation in normals (212 to 606 × 10⁶, mean 375 × 10⁶), which again is stature dependent. Alveolar counting using this method has produced similar results in rats. For example, 7- or 8-week-old Sprague-Dawley rats have been found to have a range of 40 to 70 × 10⁶ alveoli by different observers.^10,11,13,14

The selector (dissector of unknown thickness) method of Cruz-Orive²¹ has now become popular. In this method, the average volume of an alveolus, 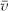, can be found and the total number of alveoli in the lung can be calculated as 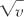, where Va is alveolar volume determined by point counting, knowing the total volume of the lung. This method has found 4.2 × 10⁶ alveoli in the mouse, 19.7 × 10⁶ in the rat, 64.9 × 10⁶ in the rabbit, and 494 × 10⁶ in the human.22 The method requires serial sections for accurate recognition of alveoli, and several sections are needed to apply the method.²³ One application of this method to abnormal and normal Sprague-Dawley rat lung development has produced results quite similar to those reported using the Weibel-Gomez technique.

The radial count is a simple technique that is quickly performed and is an integral part of the assessment of lung hypoplasia.^24–28 Using standard histological preparations, a line is dropped at right angles from the most distal respiratory bronchiole to the closest margin of the acinus, preferably a lobular septum or vein, but bronchi and arteries also suffice. The number of alveoli that have been intercepted along that line are then counted. A formal study of this method²⁵ has indicated that standard procedures must be used if between- and within-observer variations are to be minimized. It should be noted that inflated lungs produced a higher value than that produced by Emery and Mithal.^24,25 The major application of this technique is in assessing hypoplasia of the lung, whereby the complexity of the acinus and alveolar development are examined.

Sampling

It is important to sample the lung randomly because the methods used imply that the structures in the lung are randomly distributed through it. The Cavalieri system has been widely used as a method for appropriate sampling of the lung.²⁹ It is also advantageous to use the minimal number of samples required to provide satisfactory data. A running or accumulated mean and standard error are calculated and should be done when first adopting a method.⁵

If the lung is large (e.g., human) and the object of interest (e.g., type II cells) is small, it is advantageous to sample at various levels, giving a cascade type of data acquisition:

1. Sampling the gross specimen of the lung is performed first, which may involve sampling of the lung, for example, into parenchyma (the zone in which one may be interpreted) defined in a particular way, and nonparenchyma, in which one is not interested. Thus, V_par/V_lung = P_par/P_lung, where P_par is points over lung parenchyma and P is the points over the lung, and in this way the volume of parenchyma, V_par, is determined.

2. The parenchyma may then be sampled by light microscopy, and the volume density of some structure, for example the alveolar wall, measured. The volume density of alveolar wall is thus P_alvw/P_par, where P_alvw are the points over alveolar wall, and P_par are the points over parenchyma as defined. This obtains V_valvw, and hence V_alvw when multiplied by V_par.

3. The alveolar wall may then be sampled electron microscopically for an item of interest, such as type II cells. This is determined by P_{type II}/P_alvw wall, where P_{type II} are points over type II cells and P_alvw are points over alveolar wall. This gives V_v type II cells, which in turn when multiplied by V_alv wall, give the volume of type II cells. If the average volume, 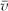, of type II cells is known, then the total number of alveolar cells can be determined.

This is obviously a very simple, nonrigorous description, but it typifies the principle of sampling at levels. The cascade method has been used with computed tomography (CT) scans (to replace whole lung) and lung biopsy material.^30,31

Other Factors

Stay updated, free articles. Join our Telegram channel

Join