Pulmonary Gas Exchange
Joan G. Matthews
Overview of Gas Exchange
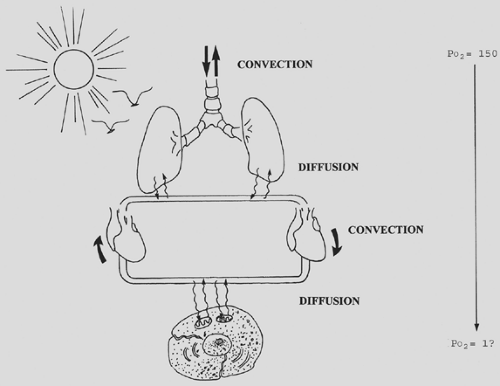
At the cellular level and in very simple organisms, oxygen is provided by simple diffusion. In more complex organisms, a more complex delivery system is necessary. The human respiratory system supplies oxygen through the combined processes of convection (bulk flow) and diffusion. The muscles of the chest wall and the conducting airways bring large volumes of gas into the alveolar space. The alveolar surface, on the order of 50 to 100 m2, provides a large area for diffusion of gas into the blood. The cardiovascular system conveys blood to the tissues, where the large combined capillary surface area facilitates diffusion of oxygen across the cell membrane and into the mitochondria. The net effect is the passive diffusion of oxygen down a partial pressure gradient from the atmosphere to mitochondria (Fig. 7-1).
Organisms also require a mechanism to eliminate the end products of metabolism. The renal and gastrointestinal systems perform this function for liquid and solid wastes, whereas the respiratory system is the site of elimination for carbon dioxide gas. The term gas exchange thus refers to both the uptake of oxygen and the elimination of carbon dioxide.
Oxygen consumption and carbon dioxide production occur in the mitochondria and vary with the metabolic state. At rest, both are on the order of 200 to 250 mL/min, but this can increase to 1 L/min with brisk walking and 3 L/min with running. Although trained athletes commonly achieve consumptions of 5 L/min, Clark and associates1 have documented transient mean oxygen consumption levels as high as 6.6 L/min in a select group of rowers.
The relative amount of carbon dioxide and oxygen exchanged is determined by the type of fuel consumed. Carbohydrate metabolism generates 1 mole of carbon dioxide for every mole of oxygen consumed. For proteins, the ratio drops to 0.8; for fats, it is 0.7. This ratio of total body carbon dioxide production to oxygen consumption is termed the metabolic respiratory quotient (RQ). In the lungs, the ratio of carbon dioxide elimination to oxygen uptake is called the respiratory exchange ratio (R). Because the lung is the site of all oxygen uptake and carbon dioxide removal in the body, lung gas exchange in the steady state is equal to tissue gas exchange, and R is equal to RQ.
Physics of Gases
Gas Phase
Both gases and liquids are fluids, a state of matter characterized by weak intermolecular forces and no fixed shape. Gases differ from liquids in that these forces are so weak that there is no fixed volume either. The ideal gas law relates the volume of a gas to the pressure, temperature, and number of moles:
where n is the number of moles, R is the universal gas constant, and T is in degrees Kelvin (degrees centigrade + 273). At constant temperature, pressure and volume are inversely proportional (Charles’s law), and at constant pressure, gas volume is directly proportional to temperature (Boyle’s law). Thus, under standard conditions of 0°C and 1 atmosphere, 1 mole of an ideal gas occupies 22.4 L (Avogadro’s law).
Dilute gas mixtures, such as air, also obey the ideal gas law, with n being equal to the total number of moles and P being equal to the sum of the pressures that each individual gas would exert in the absence of the other gases (Dalton’s law). Because the volume and temperature of all gases in a mixture are equal, it follows that the partial pressure of any gas is proportional to its mole fraction, Fx:
For oxygen at sea level, this becomes
Vapor Pressure
When a liquid is in equilibrium with its own vapor, the pressure of the gas phase is called the vapor pressure. This is the pressure at which equal numbers of gas molecules are entering and escaping from the liquid surface. The vapor pressure of a liquid is solely determined by temperature and is unaffected by baro- metric pressure. At body temperature, 37°C, the vapor pressure for water is 47 mm Hg. If dry air at 760 mm Hg is inhaled into the upper airway and held at constant volume, the pressure would increase to 760 + 47 = 807 mm Hg. This creates a driving pressure for humidified gas to flow out. Because more water will evaporate to maintain the water vapor pressure at 47 mm Hg, the net effect is that only oxygen and nitrogen are expelled, in the same ratio as their mole fraction in air: 0.79 and 0.21, respectively. Thus, at equilibrium, the pressure in the upper airway is 713 + 47 = 760 mm Hg. The partial pressure of oxygen in this setting becomes
Environmental Conditions
Because the volume occupied by any given mass of gas is dependent on its temperature, pressure, and humidity, these conditions must be specified in using volume measurements to quantify oxygen and carbon dioxide. Three conditions are commonly specified:
STPD: standard temperature and pressure, dry
ATPS: ambient temperature and pressure, saturated
BTPS: body temperature and pressure, saturated
Oxygen and carbon dioxide volumes are expressed at STPD, whereas lung volumes and ventilation are expressed at BTPS or ATPS.
Boyle’s and Charles’s laws are used to convert gas volumes from one set of conditions to another:
where T is in degrees Kelvin and P is equal to PB minus PH2O. In acid–base physiology, carbon dioxide is expressed in moles rather than volumes, obviating the need for conversion.
Gas Dissolved in Liquid
When a gas and a liquid come in contact with each other, some of the gas molecules enter the liquid and form a solution. At equilibrium, the numbers of gas molecules entering and leaving the solution are equal. The quantity of a gas contained in solution at equilibrium is described by Henry’s law:
where C is the concentration of gas in solution, P is the partial pressure in the gas phase, and α is a solubility coefficient whose value depends on the specific gas and liquid, as well as the temperature. The α for oxygen in blood at 38°C is 0.003 mL/mm Hg dL. Carbon dioxide is 20 times more soluble than oxygen in blood; the α for carbon dioxide under the same conditions is 0.06 mL/mm Hg dL.
True solubility implies that the gas molecules have not formed any chemical bond with molecules in the liquid. The quantities of oxygen and carbon dioxide that are carried in true
solution are small compared with the amounts of these gases that react chemically with the blood. The capacitance coefficient, β, includes both the gas carried in chemical combination as well as that which is in true solution. Its value is dependent on additional variables, such as hemoglobin concentration.
solution are small compared with the amounts of these gases that react chemically with the blood. The capacitance coefficient, β, includes both the gas carried in chemical combination as well as that which is in true solution. Its value is dependent on additional variables, such as hemoglobin concentration.
Even when a gas-containing liquid is not in contact with the gas phase, we still refer to the partial pressure of the dissolved gas. Although a gas in solution does not exert an actual pressure in the liquid, the partial pressure of a gas in a liquid is taken to be the partial pressure of the gas phase with which it would be in equilibrium.
Diffusion
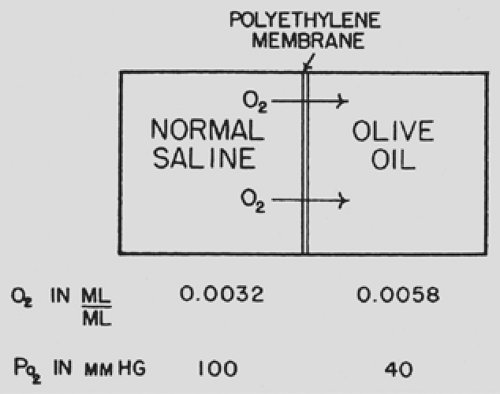
Diffusion is the net movement of particles due to random motion. Although diffusion is usually assumed to occur down a concentration gradient, it is more accurate to say that diffusion occurs from an area of high chemical activity to one of low activity. The chemical activity, or fugacity, of a gas in solution is best represented by its partial pressure. In the gas phase, partial pressure and concentration are linked in a predictable fashion. In the liquid phase, the relation between partial pressure and concentration is a function of the solubility coefficient. Diffusion of a gas between different liquids with different solubility coefficients always occurs along the partial pressure gradient, irrespective of the direction of the concentration gradient. In fact, in some instances, diffusion occurs against a concentration gradient (Fig. 7-2).
The rate of gas diffusion in the liquid phase is described by a modification of Fick’s law:
where the diffusion coefficient D of a gas is related to its molecular weight and the strength of its cohesive forces. In a liquid medium, the cohesive forces acting on a gas are increased, which makes the diffusion of oxygen in water much slower than in air (on the order of 10-5). Fick’s law applied to diffusion across a membrane implies that diffusion is greatest for a highly soluble gas across a thin membrane with a large surface area.
Factors Determining Gas Exchange in the Normal Lung
Atmospheric Gases
The composition of Earth’s atmosphere is assumed to be constant at 79% nitrogen and 21% oxygen (dry), with a negligible amount of carbon dioxide present (0.03%). Atmospheric pressure varies according to altitude and meteorologic conditions. Changes due to weather are on the order of 0.5% and do not affect respiratory physiology. Much larger variations are seen with changes in altitude. At sea level, the pressure is usually considered to be 760 mm Hg, whereas Denver, at an elevation of around 5,000 feet, has a barometric pressure of 625 mm Hg. A typical commercial airliner flies at an altitude of 29,000 feet (equivalent to the summit of Everest), where the pressure is approximately 230 mm Hg. At 33,000 feet, the pressure drops to 200 mm Hg and it is no longer possible to maintain a normal inspired PO2 while breathing 100% oxygen. At 63,000 feet, barometric pressure equals water vapor pressure, body fluids boil, and alveolar PO2 and PCO2 fall to zero.
Alveolar Gas
The partial pressure of gas in the alveolus represents a critical junction point in gas exchange. Because the mammalian respiratory system operates in a to-and-fro fashion, blood and tissue PO2 approach but can never exceed alveolar PO2. This is in contrast to the countercurrent flow design of the fish gill, where blood partial pressures approach inspired partial pressures.
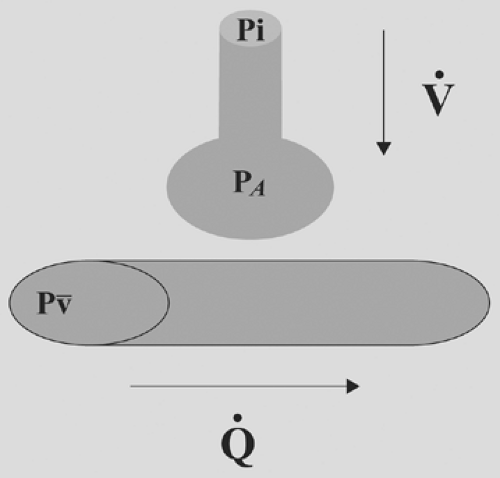
Alveolar gas composition is the result of only four variable parameters: inspired gas composition, mixed venous gas composition, alveolar ventilation, and alveolar perfusion (Fig. 7-3).
The alveolar partial pressure of a gas will lie somewhere between the inspired and mixed venous values for that gas. An increase in ventilation relative to perfusion will cause the alveolar gas composition to approach inspired, whereas an increase in perfusion relative to ventilation will cause the alveolar gas to approach mixed venous.
The alveolar partial pressure of a gas will lie somewhere between the inspired and mixed venous values for that gas. An increase in ventilation relative to perfusion will cause the alveolar gas composition to approach inspired, whereas an increase in perfusion relative to ventilation will cause the alveolar gas to approach mixed venous.
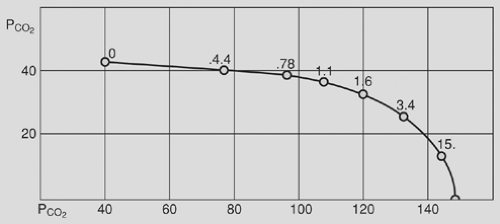
Note that alveolar gas composition is determined by ventilation and perfusion relative to one another ([V with dot above]/[Q with dot above] ratio) and not the absolute value of either. Figure 7-4 is an example of a PO2 – PCO2 diagram showing all the possible combinations of alveolar PO2 and PCO2 as a function of [V with dot above]/[Q with dot above] for a given inspired and mixed venous gas value.
Whereas all alveoli share the same inspired and mixed venous gas composition, perfusion and ventilation vary throughout the lung. In the normal lung, gravitational effects cause the [V with dot above]/[Q with dot above] to be higher at the apex than at the base. In certain disease states, the scatter of [V with dot above]/[Q with dot above] ratios is more pronounced. The efficiency of the lung as a gas exchanger is directly related to the uniformity of [V with dot above]/[Q with dot above]: A lung with all alveoli operating at the same [V with dot above]/[Q with dot above] is more efficient than a lung with [V with dot above]/[Q with dot above] mismatch. Note that the term mismatch does not imply that ventilation does not match perfusion, but rather that the [V with dot above]/[Q with dot above] ratio in one area of the lung does not match the [V with dot above]/[Q with dot above] ratio in another.
Although the nonuniformity of [V with dot above]/[Q with dot above] ratios makes it impossible to determine the gas composition of every alveolus, we can calculate the gas composition of a hypothetical ideal alveolus having the same [V with dot above]/[Q with dot above] as the lung as a whole. In this sense, we are considering the lung as a single alveolus. Any deviation from this model is evidence of nonhomogeneity of alveoli. If the [V with dot above]/[Q with dot above] ratio and mixed venous gas composition are known, then the ideal alveolar gas composition can be obtained graphically from a PO2 – PCO2 diagram like the one in Fig. 7-4.
However, these diagrams are tedious to generate, and in most clinical situations the necessary information is not available. A simpler approach is to use the alveolar gas equation for oxygen:
It derives from the observation that alveolar PO2 is equivalent to inspired PO2 (first term of equation) minus the volume of oxygen exchanged for carbon dioxide according to R (second term of equation). The third term of the equation accounts for the additional oxygen entrained when R is less than 1; it is usually ignored in dealing with room air. Because alveolar PCO2 is essentially equal to arterial PCO2 and assuming an R of 0.8, the alveolar gas equation for a patient breathing room air can be simplified to the following:
In an ideal homogeneous lung, the alveolar–arterial PO2 difference is essentially zero. Thus a large gradient between the calculated ideal alveolar PO2 and the measured arterial PO2 is an indication of nonuniformity in the lung.
Diffusion Across the Alveolar–Capillary Membrane
The alveolar–capillary membrane is perfectly designed for diffusion, with a combined surface area somewhere between 50 and 100 m2 and a membrane thickness on the order of 0.005 mm. In the normal lung, alveolar and blood PO2 and PCO2 equilibrate within the first 0.25 second, or one-third of the way along the capillary. Gases like oxygen and carbon dioxide, which reach equilibrium before exiting the capillary, are said to be perfusion-limited. Their uptake is limited only by the amount of blood delivered to the alveolus. Pathologic factors, such as loss of alveolar surface area, can cause a gas that is normally perfusion-limited to become diffusion-limited, resulting in incomplete equilibration at the end of the capillary. Some gases, such as carbon monoxide, are diffusion-limited even under normal circumstances. This is because of the physical properties of the gas itself. Gases that have a low conductance through the membrane and a high solubility in blood equilibrate slowly. The membrane-to-blood solubility ratio is a good indicator of how quickly a gas will approach equilibrium: A higher value indicates more rapid equilibration. Most inert gases (i.e., those that do not combine chemically with the blood) have ratios close to unity and equilibrate rapidly. These include nitrogen, helium, and most anesthetic gases. Carbon monoxide has a membrane-to-blood solubility ratio of much less than 1; oxygen and carbon dioxide fall somewhere in between.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree