Fig. 13.1
Graph illustrating the condition number of the material matrix [D] as the Poisson’s ratio approaches 0.5
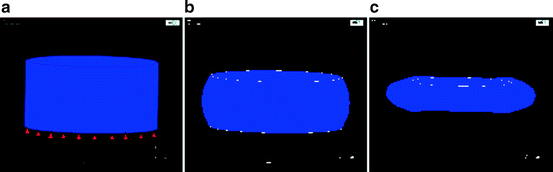
Fig. 13.2
(a) Geometry of a plug of “soft tissue;” the top surface will be subjected to a compression of 0.25 inches. (b) Simulation of “soft tissue” plug under a fixed compression; surface is subjected to a compression of 0.25 inches. Model formulation was with isoparametric linear elastic isotropic elements. The analysis fails after reaching only 45 % of the targeted compression. The simulation failure is likely due to element mesh locking. (c) Simulation of the “soft tissue” plug under a fixed compression; the top surface is subjected to a compression of 0.25 inches. Model formulation was with hyperelastic elements using a 2 parameter incompressible Mooney-Rivlin constitutive model. Model runs to completion and yields the expected deformation
13.2.2.2 Leaflet Modeling
Some of the earliest analysis of leaflets in heart valve prostheses involved numerical methods with assumptions of purely linear elastic materials [32, 33]. These methods used linear expressions for the calculation of membrane stresses. Researchers have recently found the native aortic valve leaflet is a tri-layered structure [34]. This leaflet tissue has a noted anisotropic mechanical behavior due to the circumferential orientation of the collagen fibers and the radial orientation of the elastin fibers [14]. To begin to account for this nonlinear material behavior, there have been many advances in material testing and modeling of heart valve tissue. Biaxial testing has become widely accepted for tissue material property assessment. These data provide input for constitutive models of the leaflet material. More recently, heart valve researchers have developed more customized constitutive models for valve leaflet mechanics. A good overview of leaflet constitutive models is given by Weinberg and Kaazempur-Mofrad [35], and new element formulation is also progressing. These formulations attempt to capture all aspects of the tissue in a heart valve. Weinberg and Kaazempur-Mofrad introduced a specialized shell element formulation for heart valve leaflets [36] designed to be compatible with commercial FEA codes. Sun et al. also described the necessity for accurate constitutive models when attempting to simulate the leaflets of a bioprosthetic valve [37]. This is echoed in the ISO guidance document which calls for an “…appropriate constitutive model for each material…” and that the parameters be established experimentally from material processed in the same manner as for manufacture [21].
13.2.2.3 Superelastic Material
One cannot ignore the complexity of modeling rigid crystalline metals that make up the support frames for some prosthetic valves. This is specifically true when attempting to simulate the more recent minimally invasive valve prostheses built around a superelastic material frame. Currently, heart valve prostheses manufactured with superelastic materials have been limited to Nitinol, a nickel-titanium alloy developed at the U.S. Naval Ordinance Laboratory [38]. This material has several features which are challenging to simulate [39]. Initially, in the austenitic phase, the material behaves in a linear elastic manner; when subjected to continued loading, it transforms to a martensitic phase. As the transformation progresses, the sample experiences large reversible strains with a smaller change in stress [40]. Once all the material has transformed, continued loading occurs with a modulus of the martensitic phase. Figure 13.3 illustrates a portion of a typical Nitinol load-deflection curve with cycling. Note the martensite-to-austenite reverse transformation occurs at a lower stress, defining the lower plateau. Most Nitinol material models present in the commercial finite element codes work with variants of the unified thermodynamic constitutive model for shape memory alloys developed by Logoudas et al. [41].
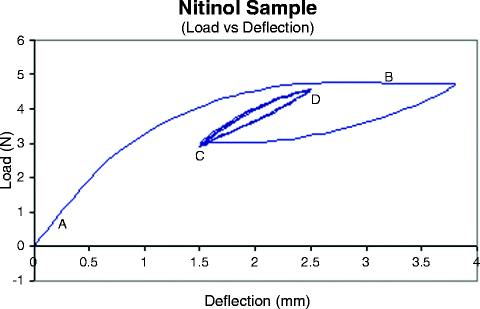

Fig. 13.3
Experimental curve illustrating the behavior of a Nitinol sample being loaded. The linear region “A” shows the linear austenite region. The plateau region “B” shows the transformation region (austenite to martensite). Note the sample was not loaded to the end of the upper plateau. The flat region between the end of the upper plateau and point “C” represents a lower plateau which is a reverse transformation back to the austenite. The loop from C to D represents a cycling of a sample from the lower plateau toward the upper plateau
For an analyst working in the area of Nitinol simulation, there are a number of important considerations. Specifically, this material is very path-dependent; in attempting to simulate loading based on some simulated in vivo conditions, one needs to be cognizant of the load history of the device (e.g., crimping, implantation, and in vivo loadings). Referring to Fig. 13.4, one can see that it is possible to be at the same strain but under completely different stresses based on the history of loading.
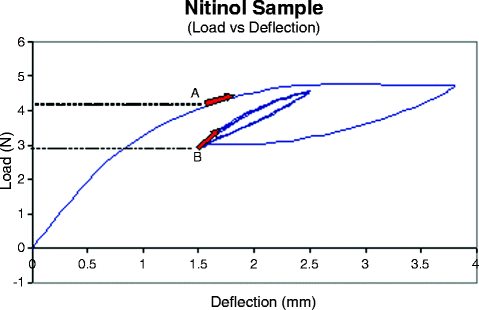

Fig. 13.4
Experimental curve illustrating the path-dependent nature for material in a Nitinol prosthetic heart valve. Loading from the origin to “A” places the material in a mixed austenite/martensite region at a high stress level. Loading from the origin to the end and then unloading to “B” places the material at the same strain level but at a different (lower) stress level. Subsequent loading from A and B will also produce different states for the material as described by the arrows
Despite its complex constitutive behavior, Nitinol is widely used in vascular stents and is proving to be a promising material in less invasive valve replacement therapies. Valve prostheses built around this emerging technology are being analyzed with available FEA tools. For example, FEA was used as a design tool in an effort to screen and optimize a heart valve design [42]. The concept was a flat sheet that could be rolled up into a stented valve and implanted percutaneously. Analyses using the new Nitinol constitutive material models helped guide the developers in their design options.
A body of work related to these materials has been performed for self-expanding arterial stents [40, 43]. Within the heart valve field, use of this material remains small, but it is expected to expand given the potential design possibilities using this unique material. The superelastic nature of the material is tantalizing for those developing percutaneous heart valve prostheses, given its ability to undergo such large strains without permanent deformation. The FDA has produced a guidance document for stents that can be utilized when considering a stent-based frame for the heart valve [44]. This document suggests specific considerations, including the degree of material nonlinearity, the uniformity of the material properties, and other variables, when simulating these materials.
When investigating the stresses and strains within a prosthetic heart valve frame, one must always be aware of the potential to load the frame beyond its elastic limit, with subsequent further plastic deformation. Balloon-expandable percutaneous frames are designed with yielding in mind—the frame is designed to intentionally yield in order to maintain its shape once deployed. When plasticity occurs, the proper work hardening model must be used to accurately incorporate the post-yield behavior. A good representation of the yield surface is required to capture any residual stresses and strains that would develop as a result of the load history of the device during manufacturing, delivery, deployment, and in vivo functioning; these stresses develop during the elastic recoil process. When analyzed with only linear elastic material formulations, these residual stresses are lost. A residual tensile stress which could develop in a highly cycled region of a frame could lead to an unexpected fracture of a supporting frame. When investigating the fracture rate in percutaneous pulmonary valve implants, researchers simulated the platinum frame with a von Mises yield surface and an isotropic hardening rule [19]. This was necessary because the transcatheter valve was a balloon-expandable valve relying on plastic deformation during deployment. This same post-yield behavior was also used by researchers simulating balloon-expandable stents [45, 46].
13.2.3 Geometry/Mesh/Element Type
Properly capturing the correct geometry is as important as the proper material definition. If one is simulating a manufactured prosthetic valve, this “geometry” may seem easy to attain but there are several features that make it more difficult. The biggest feature is variability; this becomes most important when the design is developed using automated manufacturing processes, which often include some surface finishing that is not included on the CAD drawings. For a more accurate geometric representation of a prosthetic valve, direct measurements from samples can be useful. This is true when the implant design has small features that may not be specified on the device drawing. If prototypes are available, a micro-computed tomography (CT) scan may be used to aid in the quantification of the actual geometry of a design.
Occasionally the analyst would like to simulate the actual geometry of the annular region or the vessel walls. These boundaries are then used in finite element models to simulate loading stress and strain developed from the actual implanted environment. These data are typically obtained using magnetic resonance imaging (MRI), CT, 3D ultrasound, or other imaging methods. Typically these data are collected from healthy subjects; the datasets are then converted to surfaces or element representation using various commercial software packages. These image-to-mesh methods are also touted for “patient-specific” modeling [47]. Determining geometries from data collected with these imaging methods is not without error. Uncertainties arising from imaging errors have been quantified in the past and should be included today when simulating the boundaries for heart valve prostheses.
Another consideration when representing the valve prosthesis and/or associated anatomy is symmetry. Models often rely on symmetry to reduce the number of elements in the model. Complex three-dimensional geometries will require a large number of elements to gain reasonable accuracy. Considering the materials are typically nonlinear and sometimes the analysis is dynamic, the assembly and solution time for these simulations can quickly become enormous. To make solution times reasonable, analysts often will rely on model symmetry. This is a powerful feature in finite element modeling, but the analyst must use caution and heed guidelines for the use of symmetry when creating a model. One requirement is that the geometry of the device (heart valve prosthesis) is symmetric; this is coupled with another requirement which demands that the loading conditions also are symmetric. The ISO 5840 guidance document notes that valve motion and closure is not always symmetric and recommends that analyses be performed on full valve geometries [21]. Analysts should also consider any nonuniformities that can arise in the diseased state of the anatomy. Disease can create asymmetric boundaries that invalidate the use of symmetry in a model. The FDA guidance document for analysis also requires an explanation of the appropriateness of any partial models used to represent stent-based valve prostheses [44].
Regulatory agencies have issued guidance documents for stent development and analysis; these can be referred to if the heart valve implant uses a stent-like frame for the prosthesis. These documents suggest examining different size implants and also investigating the sensitivity of the frame to the tolerances allowed for the device.
The type of element should be considered carefully when creating the finite element model. It is obvious to choose elements capable of using the appropriate constitutive model as described above (Sect. 13.2.2). Some elements will perform better than others under specific loading or contact conditions. The choice and rationale for the element type should be documented in the final report.
13.2.4 Loading Conditions (Constraints and Loads)
Properly defining the loading conditions on the prosthetic heart valve may arguably be the most difficult task facing the analyst. It is desirable for a prosthetic heart valve to perform for the lifetime of the recipient. Minimum recommended targets for device performance have been established by the regulatory bodies. ISO suggests the heart valve prosthesis be designed to withstand loads from the human body for a minimum of 10 years, while the US regulatory body, the FDA, recommends 15 years, which translates into 400 and 600 million cycles, respectively. This high cycle fatigue performance can be affected by all initial manufacturing, handling, and surgical processes; knowledge of these steps is imperative for a thorough analysis. This is specifically true if any initial procedure has the propensity to change the starting stress state in the device. For example, this can occur if a device is loaded past the material yield point during processing or handling, resulting in the development of a residual stress in the device. Therefore, before simulation of the physiologic loading on a prosthetic heart valve, one must consider the entire load history that the device will encounter prior to implant. Some of these loads may need to be included in the physiologic loading simulation because they have an effect on the stress state. This is the case with some of the new stented heart valves, and the FDA guidance on stents highlights the consideration of all loading steps [44]. The FDA specifically recommends consideration of the crimping, expansion/deployment, and any stent recoil as these steps could result in the development of a residual stress state in the stented heart valve prosthesis.
This is a good time to reflect back on the Problem Definition section (Sect. 13.2.1) to reinforce the distinction between the project goal and the model goal. The recommendations established by the regulatory bodies help establish the project goals of prosthesis survival after 400 or 600 million cycles under physiologic loading; this is a fatigue assessment requirement and currently structural finite element models cannot address this directly. FEA can, and is used to, quantify the driving force (strain amplitude, stress amplitude, stress intensity, etc.) for failure under physiologic loading.
Physiologic loading conditions are then applied to the model after the simulation of any pre-implant loading. Often the analyst is faced with the derivation of loads from assumptions on the in vivo conditions. When new devices are being examined, previously discounted loading conditions can then become important. For example, in a bileaflet mechanical valve prosthesis with a rigid housing, the propensity for radial deformations or bending is small and assumed insignificant. Depending on the design, this may not be the case for more compliant stent-based percutaneous valve prostheses where these loadings may be more significant. Analysts should consider each loading condition and determine the contribution of these conditions to the overall combined load.
The importance of these combined loadings is highlighted in the ISO guidance document [21]. For the new percutaneous transcatheter heart valves, ISO guidance recommends using blood pressures associated with Stage 2 hypertension, and suggests the manufacturer has the responsibility to identify and justify appropriate in vivo loading conditions. While it may appear simple to apply blood pressure changes in a simulation, the true use condition loads and boundary conditions are much more complex. The prostheses are being implanted in a diseased environment; annular deformations and vessel calcification change the boundary conditions and add variability. It is difficult to quantify these properties by measurements in healthy animals or humans, and there is a dearth of research focused on measuring these quantities.
13.2.5 Physics/Solution Method
The solution methods for most commercial FEA codes typically fall into one of two categories: implicit or explicit. Implicit solvers are generally used for linear or mildly nonlinear analyses, and rely on an iterative scheme to develop a converged solution for each increment. The advantage of these implicit solvers is that they allow for very large load increments, making this solver attractive for many quasi-static structural, heat transfer, and diffusion simulations. However, the iterative scheme can be computationally expensive and time consuming, and can fail for highly nonlinear problems, such as those involving contact or material, and geometric nonlinearities. This method requires some tolerance adjustments in order to overcome the nonlinearity.
Explicit solvers operate on the dynamic equations of motion by using a central difference integration scheme to explicitly develop a solution at the next time increment. This approach does not require any iteration or convergence scheme within an increment, so each increment is relatively computationally inexpensive. These solvers are particularly attractive for dynamics simulations and highly nonlinear simulations. Because no iteration is involved, a solution (good or bad) is nearly always achieved, making this solver particularly attractive for highly nonlinear quasi-static analyses typical of many implantable medical devices. Since this formulation is a wave propagation problem, certain care is needed in obtaining a quasi-static solution. However, since time is explicitly modeled, the time increment is related to the wave speed of the material and element size and is typically very short. For models with significant mesh refinement, time increments can be impractically small, requiring an unreasonable number of increments.
A variety of solution methods have been developed and implemented. Each method was designed to address a specific class of problems, with certain advantages and limitations. Selection of a solution method is important, and it is incumbent upon the user to understand these methods in order to select the most appropriate method.
13.2.6 Model Verification and Validation
Using computer predictions for prosthetic heart valve designs carries enormous importance to society. Therefore, prior to accepting the results from a finite element simulation, an appropriate level of verification and validation is required to quantify confidence in the ability of the model to represent reality. Most of the referenced simulations in this document have provided some form of validation.
Verification and validation—these two words are often referenced when speaking about numerical simulations. Unfortunately, these words are often used interchangeably despite having two very distinct meanings and guides that have been established as early as 1998 [48, 49]. Fortunately, researchers have developed sound definitions distinguishing these terms when used in reference to numerical simulations [49, 50].
Verification is the process of determining if the computational model and code correctly represent the mathematical model and its solution with sufficient accuracy. It is important to note that verification does not ensure accurate prediction of a physical event. Structural FEA and computational fluid dynamics involve the discretization of the domain into elements, and the order, type, and distribution (or bias) of these elements in large part govern the integrity and accuracy of the solution; solutions typically converge as the mesh is refined. Thus, mesh refinement is often one very important element in model verification.
A Grid Convergence Index based on Richardson extrapolation [51] has been developed and established to estimate mesh convergence error and facilitate determination of an appropriate level of mesh refinement. Adaptations by Schwer [52] allow for nonuniform grid refinement ratios. This is especially important for analyses requiring highly biased, nonuniform meshes to more effectively model areas of high gradients where an accurate assessment is needed.
With increased mesh refinement comes increased computational time and expense. As such, there is often a trade-off between mesh refinement and the desired accuracy of the solution. For example, models used for general comparative purposes that focus more on trends in behavior may not require the same level of accuracy and convergence as models intended to predict actual behavior. Analysts are responsible for establishing and verifying an appropriate level of convergence and solution accuracy commensurate with the intended use of the model [53].
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


