We read with interest the report by Chan and Redelmeier about Simpson’s paradox in medical studies. Using a hypothetical example, the investigators aimed to draw clinicians’ attention to this paradox in medical research. We would like to remind readers that the discrepancy between a crude and a stratified odds ratio (OR) actually conflates 2 different components, namely, a confounding bias and a noncollapsibility effect.
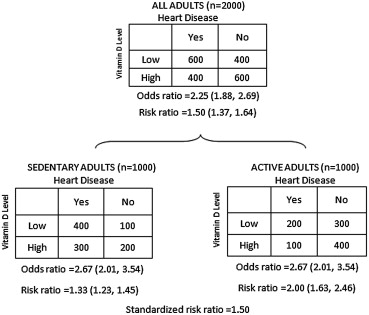
In the investigators’ example, patients’ activity levels are not balanced between the low and high strata of vitamin D level. It is clear that activity level is a confounder that is associated with vitamin D level and heart disease. Readers might therefore think that the difference between a crude OR and stratified ORs is caused only by the unadjusted confounder. However, noncollapsibility of the OR should not be neglected when interpreting the aggregate analysis. Noncollapsibility of the OR is the phenomenon whereby the crude OR from the marginal table cannot be expressed as the weighted average of the stratum-specific ORs even in the absence of confounding.
Consider hypothetical data ( Figure 1 ) adapted from the report by Greenland et al. The magnitude of the OR is different when comparing the aggregate analysis to the subgroup analysis. Note that the activity level is balanced between groups in this example (meaning that there cannot be confounding), but there is a difference between the ORs due to noncollapsibility. Therefore, we stress that the discrepancy can also arise because of the noncollapsibility effect rather than because of confounding bias only. The crude OR and the stratified OR are valid in the absence of confounding. The crude OR estimates the association in the population, while the stratified OR estimates the association in the subgroups. When we measure the association with the risk ratio, the weighted average of the stratified risk ratios equals the crude risk ratio in the absence of confounding. The disparity vanishes, because the risk ratio is a collapsible measure when there is no confounding.