Coarctation of the Aorta
Robert H. Beekman III
Coarctation of the aorta most commonly is a discrete stenosis of the proximal thoracic aorta (Fig. 45.1). However, considerable variation exists in coarctation anatomy as well as in its pathophysiology, clinical presentation, treatment options, and outcomes. For example, coarctation may be discrete or long-segment in nature, and particularly in infants may be associated with hypoplasia of the transverse aortic arch. The pathophysiology of coarctation varies with the severity of the stenosis, and also is affected by associated lesions such as patent ductus arteriosus, ventricular septal defect or left ventricular outflow obstruction. The clinical presentation of coarctation also varies, ranging from heart failure in infancy to asymptomatic hypertension in an older child or adult. Treatment options include surgical repair and percutaneous balloon angioplasty or stenting. Finally, clinical outcomes and long-term prognosis after treatment vary widely and are not entirely benign. The late prognosis can be affected by residual stenosis or arch hypoplasia, associated intracardiac pathology, aortopathy, and resting or exercise hypertension. It is correct to conclude that coarctation of the aorta is not the simple lesion it often appears to be.
Prevalence and Etiology
Coarctation of the aorta occurs in approximately 6% to 8% of patients with congenital heart disease. The New England Regional Infant Cardiac Program (NERICP) identified coarctation of the aorta as the fourth most common lesion requiring cardiac catheterization or surgery during the first year of life (1). Coarctation accounted for 7.5% of infants encountered in the program between 1969 and 1974. The prevalence is actually higher because the NERICP reported only infants requiring intervention during the first year of life. As with most left-sided obstructive lesions, coarctation occurs more commonly in males than in females, with a male:female ratio ranging from 1.27 to 1.74 (1,2).
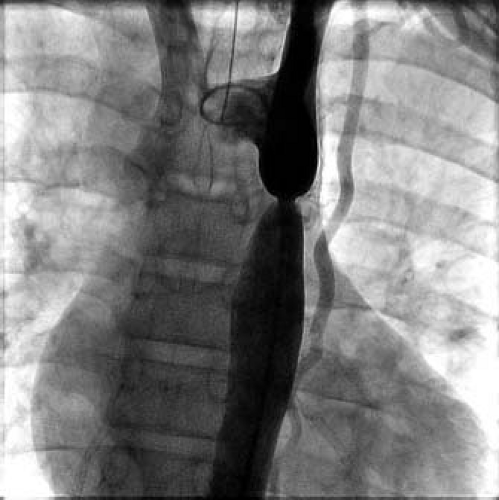 Figure 45.1 Aortogram demonstrating a discrete coarctation of the thoracic aorta. A somewhat tortuous left internal mammary artery is apparent. |
A genetic influence on the development of coarctation has long been recognized in patients with Turner syndrome (45X), in whom about 35% are affected. Interestingly, recent data indicate that approximately 5% of girls presenting with coarctation also have Turner syndrome (3). The evidence of an important genetic influence on the development of left-sided obstructive lesions is clear (4,5,6,7,8,9). For example, linkage studies have identified multiple overlapping genetic loci for left-sided obstructive lesions, including coarctation, strongly supporting the notion that these lesions are causally related (7,8). NOTCH1 mutations have been identified in some patients with bicuspid aortic valve, aortic valve stenosis, coarctation, and hypoplastic left heart syndrome (9), and more recently mutations in MCTP2 have been identified in patients with coarctation as well as hypoplastic left heart syndrome (10). Environmental influence on the development of coarctation also has been suggested by a study detecting a seasonal variation, with the incidence of coarctation peaking in the late fall and winter (11).
Embryology
The aortic arch and its branches develop during the sixth to eighth week of human gestation. The embryologic third aortic arches persist as the common carotid arteries. The left fourth aortic arch forms the thoracic aortic arch and isthmus and the right fourth arch normally involutes. The embryologic sixth aortic arches persist as the proximal pulmonary arteries, with the left sixth aortic arch developing distally into the ductus arteriosus. Thoracic coarctation is, therefore, a manifestation of abnormal development of the embryologic left fourth and sixth aortic arches (12). The underlying cause is not well understood, but two concepts have been advanced, neither of which is entirely satisfactory: the ductus tissue theory and the hemodynamic theory.
Coarctation typically occurs at the site of insertion of the ductus arteriosus. The ductus tissue theory proposes that coarctation develops as the result of migration of ductal smooth muscle cells into the periductal aorta, with subsequent constriction and narrowing of the aortic lumen (13). This concept is concordant with the clinical observations that coarctation often becomes manifest after ductus closure and that it may be palliated in the newborn with prostaglandin E1 infusion. However, the ductal tissue theory does not adequately explain some instances of aortic coarctation that occur distant from the ductus insertion.
The hemodynamic theory proposes that coarctation develops because of hemodynamic disturbances that reduce the volume of blood flow through the fetal aortic arch (14). In the normal fetus
the aortic isthmus receives only 10% of the combined ventricular output, which explains the observation that the normal neonatal isthmus diameter is only about 70% to 80% of the diameter of the ascending aorta (14). According to the hemodynamic theory, intracardiac lesions that diminish the volume of left ventricular outflow promote development of coarctation in the fetus by reducing flow through the aortic isthmus. This theory does help to explain the common association of coarctation with ventricular septal defect, aortic stenosis, and hypoplasia of the transverse aortic arch. It is also consistent with fetal echocardiographic studies demonstrating that hypoplasia of the transverse arch and isthmus are common in fetuses with coarctation (15). An interesting variation of the hemodynamic theory has been proposed to explain coarctation in girls with Turner syndrome. It is suggested that fetal lymphatic obstruction, which may cause the webbed neck in Turner syndrome, also leads to distended thoracic ducts that compress the fetal aorta and promote the development of coarctation (16).
the aortic isthmus receives only 10% of the combined ventricular output, which explains the observation that the normal neonatal isthmus diameter is only about 70% to 80% of the diameter of the ascending aorta (14). According to the hemodynamic theory, intracardiac lesions that diminish the volume of left ventricular outflow promote development of coarctation in the fetus by reducing flow through the aortic isthmus. This theory does help to explain the common association of coarctation with ventricular septal defect, aortic stenosis, and hypoplasia of the transverse aortic arch. It is also consistent with fetal echocardiographic studies demonstrating that hypoplasia of the transverse arch and isthmus are common in fetuses with coarctation (15). An interesting variation of the hemodynamic theory has been proposed to explain coarctation in girls with Turner syndrome. It is suggested that fetal lymphatic obstruction, which may cause the webbed neck in Turner syndrome, also leads to distended thoracic ducts that compress the fetal aorta and promote the development of coarctation (16).
Morphology
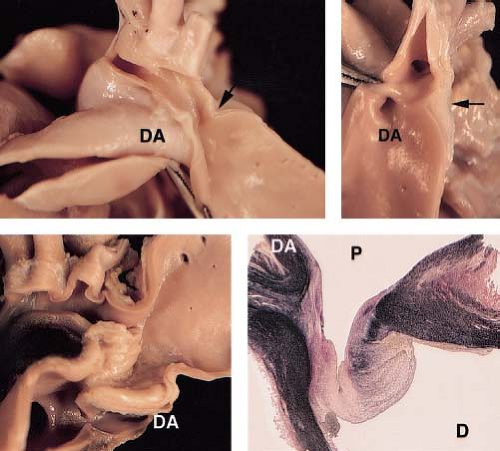
Coarctation of the aorta most commonly is a discrete stenosis in the upper thoracic aorta, at or near the insertion of the ductus arteriosus (Fig. 45.2). Most coarctations, therefore, are properly described as juxtaductal in location. The gross morphology of coarctation includes an intimal and medial malformation and a prominent posterior infolding (the posterior shelf) which often extends around the entire circumference of the aorta (17). Although coarctation is most often a discrete stenosis (Fig. 45.3), it may be long-segment and/or tortuous, and may be associated with isthmus and transverse arch hypoplasia (Fig. 45.4). Hypoplasia of the transverse aortic arch (Fig. 45.5) and isthmus proximal to the coarctation occurs often in infants, particularly those with associated left-ventricular outflow obstruction or a ventricular septal defect (18,19). Less commonly, coarctation can occur in the abdominal aorta where it may be a complex long-segment stenosis that involves the renal arteries as well (some of these cases may be the result of prior aortitis).
Histologic examination of juxtaductal coarctation reveals thick intimal and medial ridges that protrude posteriorly and laterally into the aortic lumen (Fig. 45.2). Associated intimal thickening and hyperplasia is particularly prominent in older patients (17). The ductus or ligamentum arteriosus inserts at the same level anteromedially. Intimal proliferation and disruption of elastic tissue may occur distal to the coarctation (the jet lesion), where high-velocity flow impacts the arterial wall. It is this distal site where infective endarteritis, intimal dissections, or aneurysms may occur. Cystic medial necrosis, consisting of depletion and disarray of medial elastic tissue, occurs commonly in the aorta adjacent to the coarctation site (20) and in the ascending aorta as well. In some patients, cystic medial necrosis provides the histologic substrate for late aortic aneurysm formation or dissection.
Associated Lesions
Coarctation of the aorta may be associated with other congenital intracardiac defects in some patients. Children who present in infancy are much more likely than older patients to have an associated ventricular septal defect and/or left ventricular outflow obstruction. Ventricular septal defects associated with coarctation include the perimembranous, muscular, or malalignment types. With a malalignment ventricular septal defect, posterior deviation of the conal septum may cause significant left ventricular outflow tract obstruction (21,22). A bicuspid aortic valve occurs in up to 80% of patients with a coarctation, and the valve may be stenotic or the annulus hypoplastic. Mitral stenosis also occurs in patients with coarctation and may be caused by a supravalvar mitral ring, thickening and dysplasia of the mitral leaflets, short dysplastic chordae tendineae, or the presence of a single “parachute” papillary muscle (23). The association of multiple left-sided obstructive lesions with coarctation has been referred to as Shone syndrome (24), and constitutes a challenging group of lesions when treatment is required in infancy. Other intracardiac anomalies that may be associated with coarctation include atrioventricular septal defect, d-transposition with or without tricuspid atresia, the Taussig–Bing type of double-outlet right ventricle, and congenitally corrected transposition. Coarctation also is an important component of the hypoplastic left heart syndrome.
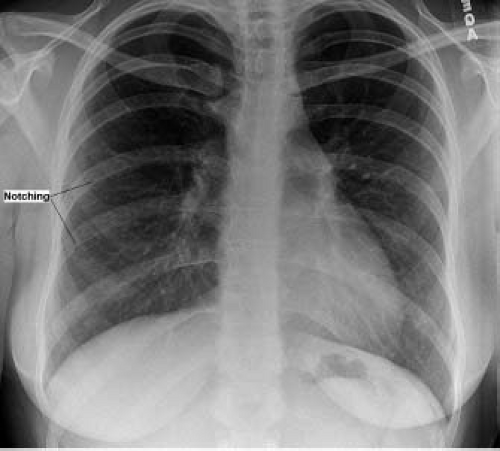
Extracardiac vascular anomalies often are present in patients with coarctation, and include variations in brachiocephalic artery anatomy, a collateral arterial circulation, and aneurysms of the circle of Willis. Thoracic coarctation usually occurs just beyond the origin of the left subclavian artery, but variations in the brachiocephalic arterial vessels may occur. The left subclavian artery may arise at the site of coarctation and may be stenotic at its origin. The right subclavian artery arises anomalously below the coarctation, as the last brachiocephalic branch, in 4% to 5% of cases. Reverse vertebral artery flow to a subclavian artery arising at or below a coarctation may produce the subclavian steal syndrome. A collateral arterial circulation, augmenting perfusion to the descending aorta, may develop by childhood or adolescence but rarely is present in infancy. This collateral system is composed of an anterior and a posterior component. The anterior circulation develops between internal mammary arteries and the external iliac arteries via the epigastric arterial system. The posterior collateral circulation develops between the thyrocervical arteries and the descending aorta via retrograde flow through enlarged intercostal arteries. These intercostal arteries may become dilated and tortuous, producing palpable thoracic thrills, continuous murmurs, and rib notching on the chest roentgenogram. Finally, saccular (“berry”) aneurysms occur in the circle of Willis in 3% to 5% of patients with coarctation. These may be responsible for cerebral vascular accidents in some patients with arterial hypertension.
Extracardiac nonvascular anomalies also may occur in patients with coarctation. In addition to Turner 45X syndrome, abnormalities of the musculoskeletal system, genitourinary system, gastrointestinal system, or respiratory system are present in as many as 25% of children with coarctation (1,25). There is also an increased incidence of head and neck abnormalities in patients with coarctation, raising the possibility that a neural crest abnormality may be involved in the embryogenesis of coarctation (26).
Hemodynamics
Fetal hemodynamics rarely are disturbed by the presence of a coarctation because normally only 10% of the combined ventricular output traverses the aortic isthmus in utero. After birth, however, with closure of the foramen ovale and ductus arteriosus, a substantially larger volume flow must cross the stenotic aortic segment. Therefore, important hemodynamic disturbances may occur postnatally. Depending on the severity of coarctation and the presence of associated cardiac lesions, these hemodynamic changes range from mild systolic hypertension to severe heart failure and shock.
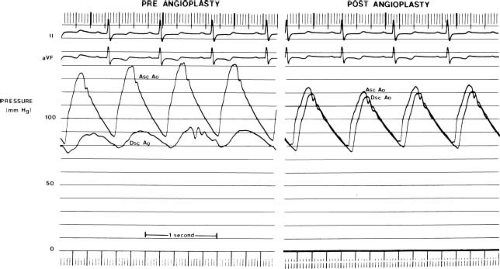
Coarctation of the aorta increases impedance to left ventricular outflow, and elevates systolic pressure in the left ventricle, the ascending aorta, and its branches. Depending on the severity of the stenosis, the cardiac output, and the extent of the collateral circulation the systolic pressure gradient across a coarctation may be as high as 50 to 60 mm Hg at rest. In many patients, a pressure gradient is present throughout systole and diastole (Fig. 45.6). A variety of compensatory mechanisms assist the left ventricle in response to the increase in outflow impedance. Left ventricular myocardial hypertrophy is perhaps the most important. Myocardial hypertrophy tends to normalize myocardial wall stress and ventricular afterload (27) and helps maintain normal systolic ventricular function. In isolated coarctation left ventricular end-diastolic volume is relatively normal, and the end-systolic volume may be reduced. Thus, left ventricular ejection fraction is normal to increased in most children with coarctation of the aorta (in the absence of heart failure).
If a coarctation is severe or develops rapidly, as in a newborn upon ductal closure, left ventricular systolic dysfunction and heart failure may ensue. The hemodynamic consequences include diminished stroke volume, increased left ventricular end-diastolic pressure, elevated left atrial pressure, pulmonary venous congestion, and pulmonary artery hypertension. If cardiac output is severely compromised, diminished myocardial perfusion and the development of acidosis depress myocardial contractility further. This clinical scenario is particularly common in the first weeks of life. Compensatory mechanisms include activation of the sympathetic nervous system (to increase heart rate and enhance myocardial contractility) and the Frank–Starling mechanism (to increase left ventricular end-diastolic volume and help maintain a normal stroke volume). The immature myocardium, however, is relatively ineffective in using these compensatory responses (28). The neonatal myocardium lacks mature sympathetic innervation as a result, in part, of a decrease in beta-receptor density. Further, compared with the adult myocardium, the neonatal left ventricular myocardium is poorly compliant and less able to enlist the Frank–Starling mechanism to preserve stroke volume. Finally, with severe coarctation in the newborn left ventricular pressure overload occurs rapidly, upon closure of the ductus arteriosus, without time for myocardial hypertrophy to develop. Left ventricular afterload and wall stress, therefore, increase in a relatively uncompensated fashion. It is clear that many factors make the immature myocardium particularly vulnerable to the hemodynamic disturbances imposed by severe coarctation, and explain the observation that ventricular systolic dysfunction and heart failure are confined primarily to the first weeks of life.
Coarctation also may cause left ventricular diastolic dysfunction. Echocardiographic studies have demonstrated a decreased rate of early left ventricular diastolic relaxation, with consequent abnormalities in diastolic filling characterized by a shift of left ventricular filling into late diastole (29). These abnormalities in diastolic function are believed to relate to diminished left ventricular compliance caused by myocardial hypertrophy, myocardial fibrosis, and, possibly an increase in the inotropic state of the myocardium. An important functional consequence is an increase in left ventricular end-diastolic pressure at any given filling volume. Thus, left atrial hypertension and pulmonary venous congestion may occur, particularly in patients with an increased left ventricular end-diastolic volume.
An associated congenital intracardiac defect compounds the hemodynamic burden in some patients with a coarctation. Valvar or subvalvar aortic stenosis will increase the left ventricular systolic
pressure and ventricular afterload further. A large ventricular septal defect, patent ductus arteriosus, or mitral regurgitation will increase left ventricular end-diastolic volume and ventricular preload. In concert with diminished left ventricular compliance, the augmented diastolic volume leads to an increase in left ventricular end-diastolic pressure. Subsequently, left atrial pressure will rise, and pulmonary venous and arterial hypertension may develop. Therefore, heart failure and pulmonary artery hypertension are relatively common in children with coarctation and associated aortic stenosis and/or ventricular septal defect as a consequence of disturbances in left ventricular preload, afterload, and diastolic function.
pressure and ventricular afterload further. A large ventricular septal defect, patent ductus arteriosus, or mitral regurgitation will increase left ventricular end-diastolic volume and ventricular preload. In concert with diminished left ventricular compliance, the augmented diastolic volume leads to an increase in left ventricular end-diastolic pressure. Subsequently, left atrial pressure will rise, and pulmonary venous and arterial hypertension may develop. Therefore, heart failure and pulmonary artery hypertension are relatively common in children with coarctation and associated aortic stenosis and/or ventricular septal defect as a consequence of disturbances in left ventricular preload, afterload, and diastolic function.
Abnormalities in peripheral vascular physiology also occur in patients with coarctation. Systolic arterial hypertension is a manifestation of the coarctation stenosis, but it also reflects changes in vascular reactivity, arterial wall compliance, and baroreceptor function. Studies of patients after coarctation repair have demonstrated abnormal arterial vascular function (30,31,32), as well as resetting of the baroreceptor reflex in some patients with persistent hypertension (33). Such abnormalities in arterial physiology, which may be present after successful anatomic relief of coarctation, help to explain the occurrence of systolic hypertension in some patients many years after coarctation repair.
Clinical Features
The clinical presentation of coarctation generally follows one of three patterns: an infant with congestive heart failure, a child with a heart murmur, or a child or adolescent with systemic arterial hypertension. When coarctation presents in infancy, it often presents as a catastrophic illness. Congestive heart failure and shock can occur suddenly as the ductus arteriosus closes. A large proportion of these infants have coarctation with important associated structural lesions such as a ventricular septal defect or aortic stenosis. In an infant with severe coarctation and a large ventricular septal defect, the sudden onset of ventricular dysfunction, low cardiac output, shock, and acidosis classically develops around 8 to 10 days of life. Multiorgan system failure, particularly renal failure and/or necrotizing enterocolitis, and death occur rapidly unless definitive medical and surgical interventions are provided rapidly.
Coarctation of the aorta may present later in childhood as systolic upper extremity hypertension or as a heart murmur. Delayed diagnosis beyond infancy is common as physical findings may be subtle, and most of these patients are asymptomatic. On careful investigation, some will report lower extremity claudication with exercise or frequent headaches. In a review of children (beyond infancy) presenting with coarctation at Columbia University between 1969 and 1978, the median age at diagnosis was 10 years. The most common causes for referral were hypertension or a heart murmur. The correct diagnosis of coarctation was made by the referring physician in only 14% of cases (34).
Physical Examination
The general appearance of a child with coarctation will vary depending on the mode of presentation. In an infant with heart failure one encounters a pale, irritable child in respiratory distress. Tachycardia, dyspnea, diaphoresis, hepatomegaly, and poor perfusion signal the presence of congestive heart failure and low cardiac output. Differential cyanosis may be observed (cyanosis confined to the lower extremities) if a right-to-left ductal shunt is present. In contrast, an older child with coarctation may appear entirely healthy. The characteristic findings of Turner syndrome are evident in some girls, and include short stature, widely spaced nipples, and a webbed neck.
The hallmark physical findings in coarctation consist of discrepant arterial pulses and systolic blood pressures in the upper and lower extremities. Arterial pulses below a coarctation are diminished in amplitude and delayed in timing compared with the proximal pulses (“pulsus parvus et tardus”). Systolic blood pressure is elevated proximal to the coarctation, and a systolic pressure gradient is present between the arm and leg. Several clinical circumstances may make detection of arterial pulse and pressure discrepancies difficult. First, the systolic pressure gradient may be minimal, because the coarctation is mild, with heart failure and diminished cardiac output or with a large patent ductus arteriosus. Descending aorta flow may be maintained by a right-to-left ductal shunt and, in the presence of a large ventricular septal defect, the perfusion may be well-oxygenated and pulsatile. Second, detection of arterial pulse and pressure differences may be difficult because of variations in brachiocephalic artery anatomy. An anomalous right subclavian artery arises distal to the coarctation in approximately 3% to 4% of cases. In these patients, the arterial pulse and blood pressure are identical in the right arm and leg, and discrepancies are detected only in the left arm. In other cases, the left subclavian artery arises adjacent to the coarctation, and its orifice may be stenotic. In such patients, a bounding arterial pulse and elevated systolic pressure will be detected only in the right arm. Rarely, patients may present with an anomalous right subclavian artery and a stenotic left subclavian artery. In this uncommon situation (more common in interrupted aortic arch) arterial differences in the four extremities will not be detected, although carotid artery pulsations can be bounding.
Several findings may be noted on palpation of the precordium. Left ventricular pressure and volume overload may produce a prominent, heaving ventricular impulse at the apex. A prominent right ventricular impulse at the lower left sternal border or xiphoid occurs if there is associated pulmonary hypertension. A systolic thrill may be palpable in the suprasternal notch, but the presence of a precordial thrill is unusual in isolated coarctation and should raise suspicion of an associated intracardiac lesion. If a robust collateral system exists prominent arterial pulsations may be palpable in the intercostal areas and/or between the scapulae posteriorly.
Auscultation generally reveals normal first and second heart sounds. A constant systolic ejection click may be heard at the apex, signaling the presence of a bicuspid aortic valve. Several murmurs may be present, depending on the nature of the coarctation, associated intracardiac lesions, and the arterial collateral system. A grade 2–3/6 systolic ejection murmur originating from the coarctation itself is usually best heard at the base and the left interscapular area posteriorly. The interscapular location of the murmur helps to identify the site of coarctation as the upper thoracic aorta. If the coarctation is severe, the systolic murmur may be long and spill into diastole. Continuous murmurs may be prominent throughout the chest anteriorly, laterally, and posteriorly in patients with a well-developed arterial collateral system. Associated intracardiac lesions create other murmurs. Aortic valve stenosis will produce a systolic ejection murmur at the upper right sternal border. A ventricular septal defect or mitral regurgitation will produce a holosystolic murmur at the lower left sternal border or apex. Associated mitral stenosis or a large left-to-right ventricular shunt will give rise to a mid-diastolic rumble at the apex. Finally, a gallop rhythm may be heard in an infant with ventricular dysfunction. If the cardiac output is severely diminished, murmurs may be subtle and the gallop rhythm may be the most prominent auscultatory finding.
Electrocardiographic Features
An infant with coarctation generally has a normal electrocardiogram (35). The finding of left ventricular hypertrophy in infancy, particularly with a strain pattern of ST segment and T-wave depression, strongly suggests associated aortic stenosis or myocardial disease. The electrocardiogram of older children and adolescents will reflect the effects of long-standing left ventricular pressure overload. Left ventricular hypertrophy and left atrial enlargement
may be present. Associated intracardiac lesions also affect the electrocardiographic findings. The frontal-plane QRS axis may be left and superior with associated AV septal defect, double-outlet right ventricle, or primary myocardial disease. Left ventricular hypertrophy with strain suggests the presence of severe valvar or subvalvar aortic stenosis. Right ventricular hypertrophy that persists beyond infancy may indicate the presence of pulmonary hypertension resulting from associated lesions, such as a ventricular septal defect or mitral stenosis.
may be present. Associated intracardiac lesions also affect the electrocardiographic findings. The frontal-plane QRS axis may be left and superior with associated AV septal defect, double-outlet right ventricle, or primary myocardial disease. Left ventricular hypertrophy with strain suggests the presence of severe valvar or subvalvar aortic stenosis. Right ventricular hypertrophy that persists beyond infancy may indicate the presence of pulmonary hypertension resulting from associated lesions, such as a ventricular septal defect or mitral stenosis.
Radiologic Features
The chest x-ray of an infant with coarctation and congestive heart failure is nonspecific. Moderate to severe cardiomegaly is evident, and the pulmonary vascular markings are increased. Pulmonary vascular congestion may be indistinct and passive in nature, related to left atrial and pulmonary venous hypertension, or it may be active and related to increased pulmonary blood flow from a large left-to-right shunt. Rib notching is not present in infants because an arterial collateral circulation is not yet well developed.
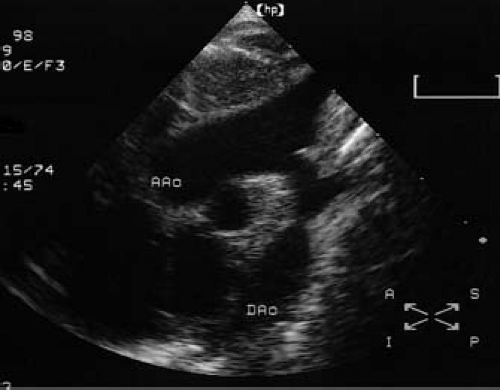 Figure 45.8 Two-dimensional echocardiogram obtained in the suprasternal long-axis view demonstrating a discrete coarctation of the aorta. AAo, ascending aorta; Dao, descending aorta. |
In older children and adolescents with coarctation, the chest x-ray typically shows a normal or only mildly enlarged heart size. The pulmonary vascular markings are normal unless there is an associated defect present. An abnormal contour of the aortic arch is common on the frontal film and consists of a localized indentation of the aorta at the site of coarctation (3 sign). Immediately below the 3 sign, the descending aorta may be prominent due to poststenotic dilation. Rib notching may be found in older patients. It is caused by erosion of the inferior surfaces of posterior ribs by dilated and tortuous intercostal arteries (Fig. 45.7). Rib notching may be unilateral if one subclavian artery is stenotic or arises distal to the coarctation.
Echocardiography
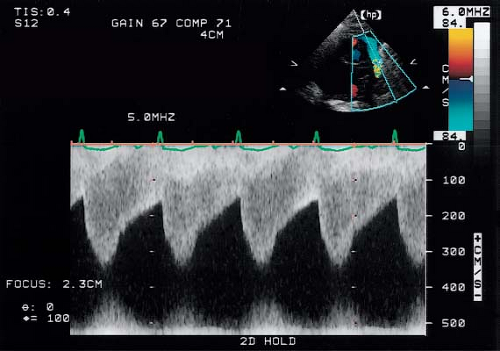
Two-dimensional echocardiography and Doppler studies can provide an accurate assessment of coarctation anatomy and physiology. High-quality ultrasound images of coarctation can be obtained in infants but may be somewhat difficult to obtain in larger children and adolescents. From the suprasternal long-axis view, typical thoracic coarctation appears
as a localized stenosis just beyond the origin of the left subclavian artery (Fig. 45.8). The narrowing appears as a shelf of fibrous tissue protruding from the posterior aspect of the aorta and oriented toward the ductus arteriosus (the “posterior shelf”). Associated findings such as isthmus and transverse arch hypoplasia, poststenotic dilation, and diminished systolic pulsations in the descending aorta serve to confirm the presence of a significant coarctation. Color-flow Doppler assists in localizing the site of obstruction and is particularly helpful in cases where two-dimensional imaging is difficult or inconclusive.
as a localized stenosis just beyond the origin of the left subclavian artery (Fig. 45.8). The narrowing appears as a shelf of fibrous tissue protruding from the posterior aspect of the aorta and oriented toward the ductus arteriosus (the “posterior shelf”). Associated findings such as isthmus and transverse arch hypoplasia, poststenotic dilation, and diminished systolic pulsations in the descending aorta serve to confirm the presence of a significant coarctation. Color-flow Doppler assists in localizing the site of obstruction and is particularly helpful in cases where two-dimensional imaging is difficult or inconclusive.
Doppler echocardiography can assist in determining the hemodynamic severity of a coarctation. A continuous-wave Doppler study from the suprasternal window will detect high-flow velocity across the stenosis (Fig. 45.9). A peak instantaneous pressure gradient may be determined from the maximal flow velocity using the modified Bernoulli equation. The Doppler-flow display across the coarctation often demonstrates a pattern of diastolic runoff, particularly in patients with a severe stenosis or with a robust collateral circulation. The continuous wave Doppler flow profile across a coarctation is composed of two superimposed signals representing low-velocity flow in the proximal descending aorta (proximal to the coarctation) and higher-velocity flow across the coarctation itself. A corrected gradient is obtained by subtracting the proximal gradient from the gradient at the coarctation site (36).
Two-dimensional and Doppler echocardiography is particularly important in evaluating intracardiac lesions that often are associated with coarctation. High-quality echocardiographic studies yield sufficient anatomic and physiologic data to enable the clinician to make a comprehensive diagnosis without the need for further diagnostic imaging in most patients.
Magnetic Resonance Imaging and CT Angiography
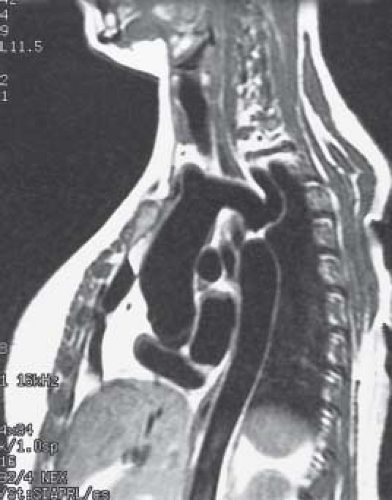
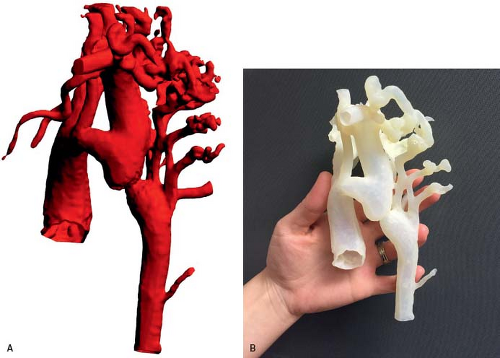
Magnetic resonance imaging (MRI) can provide very high-quality images of coarctation. MRI images in the sagittal and parasagittal projections can demonstrate the location and severity of coarctation (Fig. 45.10), and the anatomy of the aortic arch. Information about the presence of a patent ductus arteriosus and the collateral arterial circulation also may also be obtained. Three-dimensional surface rendering can provide exquisite anatomic detail in these patients (37), and three-dimensional printed models from the same MR
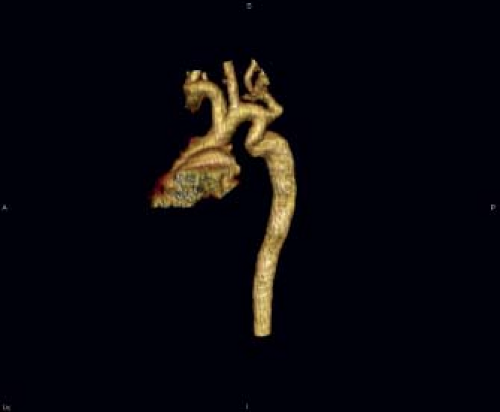
datasets provide a unique opportunity to plan surgical and transcatheter interventions (Fig. 45.11). MRI studies are particularly suited to patients who require high-resolution serial imaging, such as before and after surgical repair, angioplasty, or stenting (38). MRI studies can also provide an assessment of aortic flow, and can estimate pressure gradients (39). Multidetector CT angiography also provides excellent anatomic information in patients with coarctation and aortic arch anomalies (Fig. 45.12). CT angiographic data are acquired very rapidly (typically in 4 to 5 seconds) as gating is not required as with MRI studies. Unlike MRI examinations, however, CT angiography exposes the patient to ionizing radiation.
datasets provide a unique opportunity to plan surgical and transcatheter interventions (Fig. 45.11). MRI studies are particularly suited to patients who require high-resolution serial imaging, such as before and after surgical repair, angioplasty, or stenting (38). MRI studies can also provide an assessment of aortic flow, and can estimate pressure gradients (39). Multidetector CT angiography also provides excellent anatomic information in patients with coarctation and aortic arch anomalies (Fig. 45.12). CT angiographic data are acquired very rapidly (typically in 4 to 5 seconds) as gating is not required as with MRI studies. Unlike MRI examinations, however, CT angiography exposes the patient to ionizing radiation.
Cardiac Catheterization and Angiography
Cardiac catheterization can serve both diagnostic and therapeutic purposes in patients with a coarctation. Diagnostic cardiac catheterization is unnecessary if noninvasive evaluation clearly delineates the lesions that are present. If important clinical questions remain regarding the nature and severity of a coarctation or associated intracardiac lesions, a diagnostic cardiac catheterization may be valuable. The objectives of a diagnostic cardiac catheterization in a patient with coarctation are to define the anatomy and severity of the coarctation, evaluate aortic arch anatomy, the arterial collateral
circulation, the presence and severity of associated lesions, left ventricular function, and pulmonary artery pressure and resistance.
circulation, the presence and severity of associated lesions, left ventricular function, and pulmonary artery pressure and resistance.
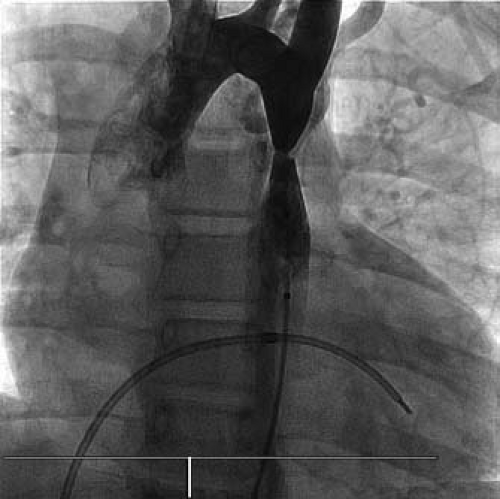
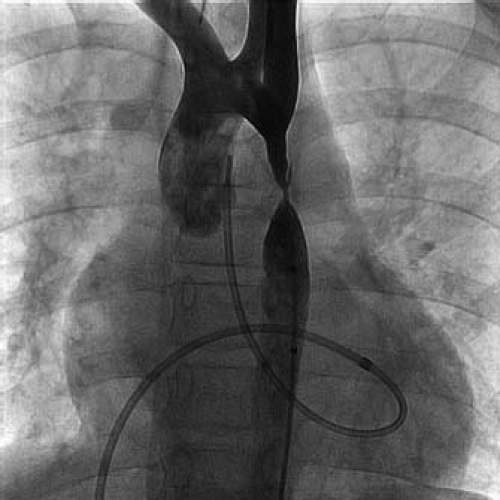
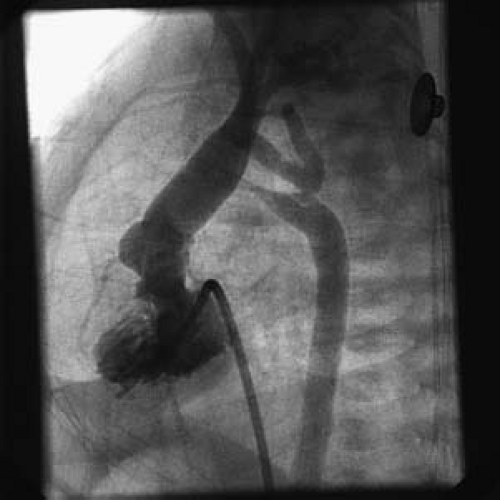
Coarctation causes an elevated systolic pressure within the ascending aorta and a diminished systolic pressure and pulse pressure in the descending aorta (Fig. 45.6). In a child with an isolated coarctation and a normal cardiac output, a systolic gradient less than 20 mm Hg is often indicative of mild coarctation. However, pressure gradient alone may underestimate a coarctation. The pressure gradient may be diminished with left ventricular dysfunction and low cardiac output, by a patent ductus arteriosus, by other left-sided obstructive lesions in series, or by an arterial collateral circulation that decompresses the ascending aorta. Thus, the hemodynamic importance of a measured coarctation gradient must be assessed in the context of the patient’s overall anatomy and physiology.
Angiography remains a gold standard for evaluating coarctation and aortic arch anatomy. The anatomy of the coarctation and collateral circulation generally is best imaged by an ascending aortogram filmed in the anteroposterior and straight lateral projections. In some patients, the anteroposterior camera is rotated 10 to 15 degrees left anterior oblique (LAO) to unwrap the ascending from the descending aorta. If the ascending aorta is not catheterized, the coarctation anatomy may be visualized satisfactorily in some patients with a left ventricular angiogram alone.
Natural History and Management
Patients with untreated coarctation have a poor natural history, characterized by significant morbidity and early mortality. In his classic 1970 study, Campbell reported natural history data obtained from necropsy and clinical records on 465 patients with coarctation (40). Only subjects who survived the first year of life were evaluated, excluding infants with critical coarctation. Nevertheless, Campbell’s natural history data for untreated coarctation beyond infancy documented a mean age at death of 34 years (median, 31 years), with 75% of patients having died by 46 years of age. The most common causes of death were congestive heart failure (26%), aortic rupture (21%), endocarditis (18%), and intracranial hemorrhage (12%). Given such a poor prognosis untreated, it is apparent that intervention is indicated in virtually all patients with coarctation of the aorta. The timing of therapy depends on the nature of the patient’s presentation.
Presentation in Infancy
Coarctation presenting with heart failure in infancy requires immediate treatment. Medical management consists of initially stabilizing the patient with inotropic support. A critically ill newborn also may benefit from prostaglandin E1 to promote ductal patency and improve perfusion of the descending aorta, renal, and mesenteric beds (41). Metabolic disturbances such as acidosis, hypothermia, hypoglycemia, or anemia must be treated promptly. After a brief period of medical management to stabilize the child, definitive repair should be performed (42). In experienced centers, the mortality rate for surgical repair of isolated coarctation in infancy is very low (43,44,45,46,47,48,49,50,51).
The surgical risks are higher for infants with coarctation who have associated major intracardiac anomalies. Nevertheless, after a period of medical stabilization, early coarctation repair is indicated in these children. The surgical mortality rate for these infants ranges from 2% to 10% and is highest for children with the most complex intracardiac defects (43,44,45,46,48,51). The need for intracardiac repair (or pulmonary artery banding) at the time of coarctation repair is not always clear. In some circumstances, coarctation repair alone is sufficient and may improve the pathophysiology of the associated lesion. For example, following repair of coarctation an infant with a ventricular septal defect may demonstrate a diminished left-to-right shunt and resolution of heart failure. Subsequently, some will experience spontaneous diminution in size of the ventricular septal defect sufficient to avoid future intracardiac surgery. Modest hypoplasia of the aortic arch, aortic or mitral valves may improve in follow-up after repair of coarctation in the newborn (52). Intracardiac repair at the time of coarctation repair is appropriate in infants with a large ventricular septal defect, or more complex lesions such as d-transposition or double-outlet right ventricle (53,54).
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree