We thank Pang et al for their insightful comments about noncollapsibility, a mathematical phenomenon unrelated to confounding whereby the odds ratio of a total cohort does not equal the weighted average of the odds ratios in the relevant subgroups. This poorly understood and grossly underreported nuance in clinical research tends to render aggregate odds ratios more conservative (i.e., biasing results toward the null) and can contribute to misinterpretation of outcomes in clinical trials.
One factor contributing to the neglect of statistical anomalies is the awkward terms for communicating the same concept in different fields. Noncollapsibility is similar to the fallacy of composition (e.g., an assembly of the world’s best musicians does not necessarily lead to the world’s best orchestra). It is also reminiscent of Arrow’s paradox (e.g., every integrated ranked voting system is flawed) and the modo hoc syllogism (e.g., an athlete can lose each single event yet still win the Olympic decathlon). All these terms are excluded from formal medical training and thereby escape the attention of most clinicians.
One way for clinicians to gain an intuitive understanding of noncollapsibility is to appeal to a famous triad exemplifying faulty reasoning. Namely, (1) individual human cells are invisible to the naked eye; (2) a human being is composed of individual human cells; and (3) therefore, a human being is invisible to the naked eye. This faulty reasoning triad of noncollapsibility is easy to grasp when considering a concrete case. The same anomaly, however, can be mystifying when interpreting subgroups in medical research.
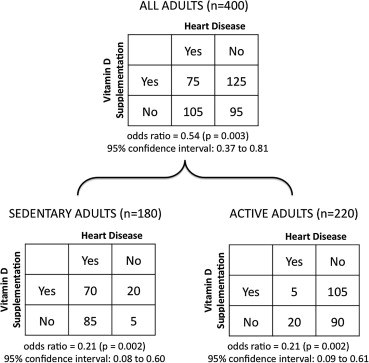
Consider a less transparent example of noncollapsibility based on a hypothetical randomized trial (n = 400) of vitamin D supplementation for preventing heart disease ( Figure 1 ). The aggregate results of this hypothetical trial show that treatment leads to a significant risk reduction (38% vs 53%, p = 0.003), equal to an odds ratio of 0.54 (95% confidence interval 0.37 to 0.81). Hence, a naive supposition is that subgroup analyses should yield similar odds ratio estimates (albeit with more random variation).