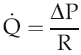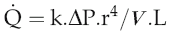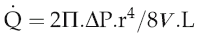Chapter 5 Vascular system

The volume flow of blood around the circulation per unit time (

) can be expressed in terms of the pressure gradient (ΔP) and the absolute resistance to flow of the vasculature (R):

Intravascular pressure at the downstream end of the vascular circuit where it drains into the heart is virtually the same as atmospheric pressure and can be regarded as 0 mmHg. The value of ΔP, therefore, depends primarily on the value of arterial blood pressure. In the last chapter we looked at the aspects of cardiac function that affect this and reviewed briefly the involvement of the peripheral vasculature. We need now to examine in more detail the properties of blood vessels and how these contribute to resistance to flow.

PHYSICAL FACTORS AFFECTING PERIPHERAL RESISTANCE

Vessel length

The pressure of fluid flowing through a tube falls progressively along the tube, due to friction between the fluid and the tube wall. Thus, vessels of different lengths must contribute differently to overall peripheral resistance, with short vascular beds such as that of the stomach having less resistance (and correspondingly faster circulation times) than those of the limbs.

Even though some vessels travel in the walls of organs that change size dramatically, such as the bladder, stretching of these organs does not alter the length of the vessels. When the organs are at their minimum volume, the vessels are coiled and stretching just straightens out these coils.

Vessel radius

Since there is friction between a flowing fluid and the tube in which it is contained, the ratio between the cross-sectional area and the surface area of the tube constitutes a second determinant of resistance. This means that small tubes have higher resistance per unit length than large tubes. Because the critical factor is cross-sectional area rather than radius, resistance changes in proportion to the fourth power of the radius, with the result that only small incremental changes in vessel size confer very large changes in resistance. For example, halving the radius would increase resistance 16-fold.

The fact that resistance is greater in small vessels indicates that absolute resistance must be lower in veins than in arteries, since all segments of veins are around twice the size of the equivalent arterial vessels. The relatively low venous resistance is essential for efficient circulation, since the role of the venous system is simply to drain blood back to the heart as rapidly as possible and is reflected in the fact that the same left cardiac output requires a pressure gradient of around (100–30) or 70 mmHg to deliver it to the capillaries but only (20–0) or 20 mmHg to return it from the capillaries to the heart.

The dependence of resistance on absolute vessel size also indicates that the major component of total peripheral resistance must be localized to the smaller precapillary vessels (the microcirculation) rather than the large distributing arteries. Not only are these microcirculatory vessels smaller in radius but they also branch repeatedly every mm or so. Although total cross-sectional area increases with each branching, total surface area increases even more, so that resistance rises rapidly along quite a short distance.

While most textbooks talk about the arterioles as being the primary site of peripheral resistance, this is an oversimplification. The arterioles are the smallest of the precapillary vessels, with luminal diameters of 200 μm or less, but in fact all the small muscular arteries less than around 1 mm in diameter that give rise to these arterioles also constitute a major source of resistance.

What may appear paradoxical is that the high resistance is restricted to the precapillary vasculature, while systemic capillaries have diameters of around 7 μm and so are rather narrower than even the smallest arteriole, yet impose less resistance to flow. The lower resistance in capillaries than arterioles reflects the fact that several capillaries arise from each arteriole, so that the total capillary cross-sectional area:surface area ratio is very much greater than is associated with any generation of arterioles. In terms of functional efficiency, it is of course essential for local resistance not to limit flow through the capillary bed.

Blood viscosity

The viscosity of a moving fluid represents the amount of friction between the components of the fluid, in contrast to the friction that occurs by interaction of the fluid with the surrounding tube surface. Any friction will increase the amount of energy that is needed to move a fluid along a tube, so viscosity must constitute a further factor contributing to flow resistance.

Different fluids have very different viscosities – think of water and honey – but all fluids that consist only of molecules in solution have viscosities that remain constant regardless of the velocity of fluid movement. Such solutions are termed Newtonian fluids. By contrast, fluids that contain suspended material (non-Newtonian fluids) have viscosities that vary with flow velocity, being greater at low rates of movement. This property is termed anomalous viscosity. Because blood is a suspension of cells in plasma, it behaves in a non-Newtonian fashion and this has several implications.

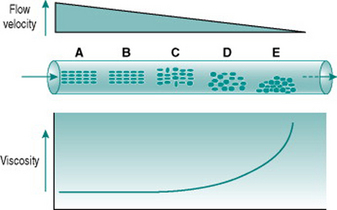
Figure 5.1 illustrates the processes that underlie anomalous viscosity in the bloodstream. When the blood is flowing relatively fast (A–B), the cellular components travel as a core in the centre of the vessel, surrounded by a cell-free layer of plasma. The cells are oriented so that they travel edge-on, producing minimal friction between the cell layers and between cells and plasma. The viscosity of the blood in this situation is around 50% greater than that of plasma alone. If the flow velocity falls sufficiently then the orientation of the suspension becomes less organized, with some cells starting to rotate and collide with adjacent cells. This process absorbs some of the energy creating the pressure gradient and so viscosity rises (C–D). If flow rate falls even further, the cellular constituents fall out of suspension and form an aggregate on the gravitationally lowest surface of the vessel. Because of the mass of the aggregate, a substantial amount of energy is required to lift the cells back into suspension again, reflected in a very high viscosity (E).

Figure 5.1 Changes in viscosity and the associated changes in red blood cell behaviour as the velocity of blood flow falls. A & B represent velocities typical of flow in the normal, intact circulation.

The dependence of blood viscosity on the cellular components has several implications. First, alteration of the haematocrit will change the size of the cell-rich core relative to surrounding plasma. Therefore, increased haematocrit will proportionately elevate viscosity. This can impose a substantial extra cardiac workload particularly during exercise. Thus, ‘blood doping’ with erythropoietin, although it is likely to improve maximal exercise performance by enhancing oxygen delivery to muscles, also carries a significant risk of damage to the heart. A second consequence of anomalous viscosity is that very low rates of blood flow can result in cells falling out of suspension. If the cell aggregates remain unsuspended for more than a few minutes, they begin to stick together and, in small vessels, may completely obstruct the lumen. This situation is most likely to occur in the postcapillary venules and will be discussed in Chapter 10 in relation to hypotensive states associated with prolonged exercise.

HANDY HINTS

The width of the cell-free plasma layer is relatively independent of vessel size, because it is dictated by the profiles of the endothelium and the blood cells. By contrast, the number of layers of blood cells that can travel in the cell-rich core must decrease progressively through the microcirculation; in the small arterioles only two or three cells will be able to travel in parallel. With a fall in vessel size, the local blood viscosity must also fall, both because there is reduced friction between the cell core and the surrounding plasma and because there is less friction between adjacent layers of cells. As a result, absolute viscosity in the smallest arterioles may be only about two-thirds that in the aorta.

This has practical implications for measurement of haematocrit during human experiments. Since the usual technique of blood sampling involves finger prick, the origin of the sample is primarily from the superficial microcirculation. It can be predicted that the haematocrit measured in this way is likely to underestimate the true value by at least several per cent and, further, that haematocrit will rise under conditions where the vessels of the finger microcirculation are dilated, such as during heat stress or exercise. Routinely warming the hand in hot water before taking finger prick samples ensures more reproducible and accurate measurements of haematocrit in resting subjects.

Blood flow through systemic capillaries is rather different to that through either precapillary or postcapillary vessels. All these other vessels have diameters greater than that of blood cells, whereas the typical capillary diameter of around 6 μm is marginally less than that of an erythrocytes (8 μm). In consequence, blood cells have to be partially folded in order to pass along the capillary. This process is important in that it ensures the closest contact possible between erythrocyte and endothelial membranes and so minimizes the distance for gas diffusion between blood and tissue. However, in theory it should also produce very high frictional forces between blood cells and the capillary wall, greatly increasing local viscosity and impeding the efficiency of capillary perfusion. To avoid such a disadvantageous situation, the endothelium of capillaries secretes a lubricant mucopolysaccharide that virtually eliminates frictional interaction with the blood cells and results in local viscosity that is almost as low as that of cell-free plasma.

Poiseuille’s law

The equation relating flow, pressure and resistance (see p. 45) can be rewritten by substitution of vessel radius (r) and length (L) and blood viscosity (V) for resistance, and adding a factor for numerical accuracy (k), thus:

This equation was derived by the scientist Poiseuille and is known as Poiseuille’s law. In its full form, with the factor k expressed numerically, it reads:

The practical importance of Poiseuille’s law is that it describes the main factors affecting the relationship between flow and pressure. It does not of course take account of homeostatic feedback so does not necessarily predict the end result of manipulating these factors in the whole body. For example, if blood pressure were elevated by a sudden increase in blood volume, there would normally be baroreflex compensation that would lower peripheral resistance and return the pressure to its initial level (see Chapter 7, p. 81). A second difference from the events in the intact circulation is that Poiseuille’s law assumes that the vasculature is a system of rigid tubes. As soon as we deal with tubes that might distend in response to internal pressure, then obviously the association between pressure and flow becomes different.

RESISTANCE TO FLOW OF DISTENSIBLE VESSELS

Roles of connective tissue and muscle in determining distensibility

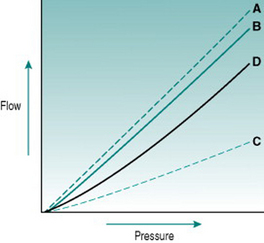
In rigid tubes, there is a linear relationship between the pressure gradient and the resulting volume flow, presuming that resistance remains constant (Fig 5.2A). In distensible tubes, by contrast, increased internal pressure will cause some increase in tube volume, so that the rate of volume flow rise with pressure will be lower. In blood vessels, distensibility is conferred by the presence of elastin in the vessel wall, while the presence of collagen confers rigidity (Fig. 5.2B–D). The property of distensibility is usually referred to as compliance.