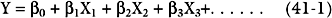General Versus Specific Risk-Scoring Systems

Risk-scoring systems may be classified as either general or specific. General scoring systems are widely used in ICU practice. Examples include the Acute Physiology and Chronic Health Evaluation (APACHE), which has undergone four iterations (I through IV); Mortality Probability Models (MPM) II; and the Simplified Acute Physiology Score (SAPS) II. With APACHE IV, mortality risk is calculated on the basis of multiple factors, including (1) acute derangements of 17 physiologic variables measured within 24 hours of ICU admission; (2) the patient’s age; (3) the presence of chronic, severe organ failure involving the heart, lungs, kidneys, liver, or immune system; (4) the admission diagnosis; (5) the pre-ICU length of hospital stay. (Downloadable risk calculators for APACHE IV are available from www.criticaloutcomes.cerner.com.) Although useful for most ICU patients, these general scoring systems are of limited value for cardiac surgery patients because many of the acute physiologic changes that occur in the first 24 hours are related to the effects of surgery and cardiopulmonary bypass and do not reflect patients’ risk for dying or suffering morbid events. Although APACHE IV has a mortality-prediction algorithm for use in patients who have had coronary artery bypass graft (CABG) surgery using postoperative day 1 variables, it may not be valid outside the United States and is not designed for use in patients undergoing other cardiac operations.² General scoring systems are not discussed further.

Specific risk-scoring systems apply to particular diseases, operations, or groups of operations. Adult cardiac surgery, which has a small number of operations, a large number of patients, and a relatively high incidence of complications, is well suited to risk-adjusted scoring. A number of cardiac risk-scoring systems are in use, including the European System for Cardiac Operative Risk Evaluation (EuroSCORE), the French score, the Cleveland Clinic score, the Ontario Province Risk Score, the Parsonnet score, and the score based on the Society of Thoracic Surgeons (STS) National Cardiac Surgery Database.

Principles of Cardiac Risk-Scoring Systems

To appreciate the strengths and weaknesses of risk-scoring systems, it is important to consider how they are developed and validated.^3–5

Development of Risk-Scoring Systems

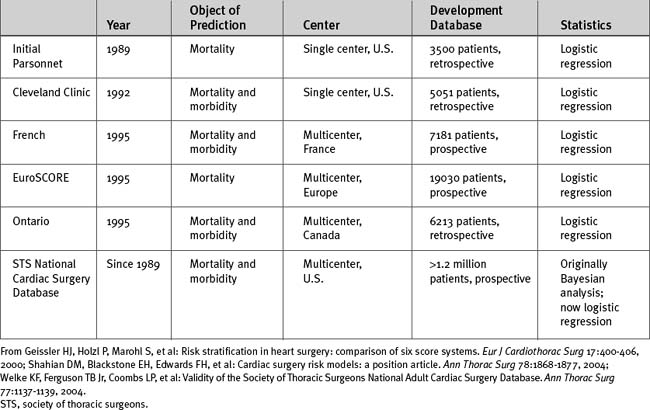
The most widely used statistical tool for developing risk models is logistic regression.⁶ First, univariate regression analysis is used to identify statistical associations between predictor variables and the outcome variable. From these variables, a multivariate logistic regression model is developed in which independent predictor variables are identified and included in a regression equation of the following general form:

(41-1)

Where Y is the outcome, β₀ is the regression constant, X₁ is a predictor variable, and β₁ is a constant, reflecting the weighting given to X₁. β₀ is typically negative (e.g., −4.789594 for the EuroSCORE), whereas β₁, β₂, β₃, etc., are typically positive and may be greater than 1. Outcome is calculated either directly, using the regression equation (logistic score) or by converting the β coefficients to integer values, which are then summed (additive score). Death is the primary outcome variable of cardiac risk scores. Some scores are also designed for morbidity prediction. Predictor variables must be chosen carefully. A large number of variables with multiple values (e.g., myocardial infarction within <6 hours; 6 to 24 hours; 1 to 7 days; 8 to 21 days; >21 days) may provide a highly accurate model but increases the likelihood of there being missing or incorrect data, leading to erroneous predictions. Variables that are likely to have missing data or are subject to observer bias should be removed from the model, even if they are independent outcome predictors. The number of predictor variables is limited by the size of the dataset from which the model is developed. As a rule of thumb, the number of deaths must be 10 times the number of predictor variables. Thus, for a mortality rate of 3%, a database of more than 5000 patients is required to develop a model with 15 predictor variables. With cardiac risk models, the number of variables ranges from 6 using the Ontario score to more than 20 using the STS score.

Other than database size, additional important issues are the time the data were collected, the geographic location of the patients in the database, whether the database is single-center or multicenter, and whether the data were collected prospectively or retrospectively (Table 41-1). For instance, the Parsonnet score—the first widely used cardiac risk-scoring system—was originally developed from a retrospective database of 3500 patients operated on between 1982 and 1987 in the United States. Given the changes in patient populations and surgical management since then, outcome predictions based on this patient population may no longer be valid, particularly outside the United States.

Table 41-1 Designs of Selected Risk Scores

Validating Risk-Scoring Systems

Once a risk model has been developed it must be validated in other patients to see whether it functions for its intended purpose and how well it applies to various populations over time. There are two major statistical approaches to evaluating the predictive accuracy of a scoring system: calibration and discrimination.

Calibration refers to how well the model assigns appropriate risk. It is evaluated by dividing patients into groups (usually deciles) according to expected risk and then comparing expected to observed risk within those groups. A well-calibrated model shows a close agreement between the observed and expected mortality rates, both overall and within each decile of risk. Most cardiac risk models are well calibrated in the midrange but less so for patients at the extremes of risk, both high and low.⁷

Discrimination refers to how well the model distinguishes patients who survive from those who die (Fig. 41-1). It is evaluated by analyzing receiver operating characteristic (ROC) curves.⁸ ROC curves are plots of sensitivity (true positive rate) against 1− specificity (false positive rate) at various levels of predicted risk (cutoffs). They graphically display the tradeoff between sensitivity and specificity as shown in Figure 41-2. For randomly selected pairs of patients with different outcomes (survival or death), a model should predict a higher mortality risk for the patient who dies than for the patient who survives. The area under the ROC curve (c-statistic) varies between 0.5 and 1.0 and indicates the probability that a randomly chosen patient who dies has a higher risk than a randomly chosen survivor. A model with no discrimination has an area under the ROC curve of 0.5 (see Fig. 41-2, graph B), meaning that the chance of correctly predicting the death in a randomly chosen pair is 50%, which is no better than the toss of a coin. By contrast, a model with an area under the ROC curve of 1 (see Fig. 41-2, graph A) implies perfect discrimination, meaning that the model always assigns a higher risk to a randomly chosen death than to a randomly chosen survival. In such a situation, there is no tradeoff between sensitivity and specificity; they are always 100% at every percentage risk prediction. A good explanation of ROC curves with applets allowing graphic manipulation of the threshold and sample population separation is given at http://www.anaesthetist.com/mnm/stats/roc/index.htm.

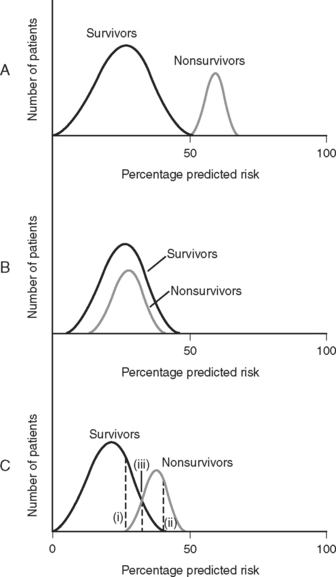
Figure 41.1 Discrimination of risk models. A, A risk model with perfect discrimination. In this example, all of the patients with a predicted mortality risk of 50% or less survive, and all of the patients with a predicted mortality risk of 50% or greater die. B, A risk model with no discrimination. C. Although an oversimplification, model C is more typical of a real-world cardiac risk model. Nonsurvivors tend to have a higher predicted mortality rate than survivors, but there is some overlap. No cutoff separates all survivors from all nonsurvivors. Line (i) represents the cutoff point corresponding to 100% sensitivity for predicting death. That is, 100% of nonsurvivors have a mortality prediction greater than line (i). Line (ii) represents the cutoff point corresponding to 100% specificity for predicting death. That is, there are no survivors beyond line (ii). Line (iii) represents the optimal tradeoff between sensitivity and specificity. Most of the patients who die have a risk score above this cutoff point, and most of the patients who survive have a risk score below this cutoff point. Sensitivity and specificity are further discussed in Appendix 2.

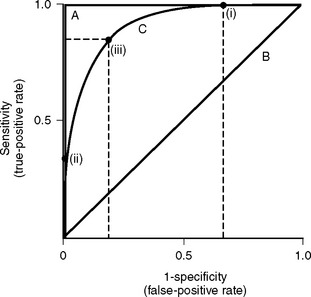
Figure 41.2 Receiver operating characteristic (ROC) curves for mortality prediction. ROC curves are constructed by plotting sensitivity (true-positive fraction) against 1-specificity (false-positive fraction) for all levels (cutoffs) of predicted risk from 0% to 100%. Three curves are shown; they correspond to A, B, and C in Fig. 41-1. For curve A, as sensitivity rises there is no loss of specificity (and as specificity rises, there is no loss of sensitivity). This model has perfect discrimination, and the area under the ROC curve is 1.0 (see text). For curve B, as sensitivity rises there is loss of specificity by an exactly equal amount, and vice versa. This model has no discrimination, and the area under the ROC curve is 0.5 (see text). Curve C is more typical of cardiac risk scores. A sensitivity of 100% is associated with a specificity of about 30% (i.e., 1-specificity of 0.7). This is shown as point (i) on curve C. A specificity of 100% (i.e., 1-specificity of 0) is associated with a sensitivity of about 30%. This is shown as point (ii) on curve C. Point (iii) represents the risk score at which sensitivity and specificity are both optimal, in this case about 80% for each. The area under curve C is about 0.85, which represents a high degree of discrimination—most risk models in medicine and surgery perform well below this. Sensitivity and specificity are defined formally in Appendix 2.

The discriminatory ability of cardiac risk scores is limited by the presence of unknown independent predictors, random catastrophic events (e.g., a severe protamine reaction), difficulty in measuring complex clinical states, and factors that are rare but if present may be prognostically important (e.g., the presence of a pheochromocytoma in a patient undergoing CABG surgery). In validation studies, most cardiac risk scores for mortality have an area under the ROC curve of 0.7 to 0.80, indicating moderate discrimination.

Choice of Risk Models

The two most important cardiac surgery risk-scoring systems currently in use are the EuroSCORE and the system developed from the STS National Cardiac Surgery Database. The STS database was established in 1989 and is the largest cardiac surgery database in the world. In 2004 there were 638 contributing hospitals, and it contained information from more than 2 million surgical procedures.^5,9 Participating hospitals submit their data to the STS on a biannual basis and receive detailed reports after analysis of the data from all participants. Reports contain risk-adjusted measures of mortality rates, which allow participating hospitals to benchmark their results against regional and national standards. The reports also provide data for research projects. Risk scoring is based on 24 patient-, cardiac-, and operation-related predictor variables. An online risk calculator is available from the STS website (www.sts.org) at http://66.89.112.110/STSWebRiskCalc/. The web calculator provides mortality predictions for five main operations: CABG surgery, aortic valve replacement, mitral valve replacement, CABG surgery plus aortic valve replacement, and CABG surgery plus mitral valve replacement. In addition, outcome predictions for five morbidities in CABG surgery are also provided: reoperation, permanent stroke, renal failure, deep sternal wound infection, and prolonged ventilation. Unlike other risk-scoring systems, the STS system has not released into the public domain the logistic regression equations it uses.

The EuroSCORE was developed from a prospective database of more than 19,000 patients involving 132 centers in eight European countries.¹⁰ Data were collected over a 3-month period in 1995. Two forms of the EuroSCORE have been developed—the additive score and the logistic score. Both are based on the same 17 predictor variables. The additive score is shown in Table 41-2. The EuroSCORE website (www.EuroSCORE.org) provides the β coefficients for the logistic regression equation and makes available online and downloadable risk calculators for the logistic score. In head-to-head comparisons, the EuroSCORE has been shown to have better discrimination than other scoring systems (i.e., a higher area under the ROC curve).^11–13 However, some investigators have found that the EuroSCORE (both additive and logistic) tends to overestimate observed mortality risk across a range of risk profiles (i.e., limited calibration).^12,14,15 This may indicate that the EuroSCORE should be recalibrated to account for changes in patients and practices since it was developed in the 1990s. By contrast, other investigators have found that the additive EuroSCORE tends to underestimate observed risk in high-risk patients^16,17 and in patients undergoing combined valve and CABG surgery.¹⁸

Table 41-2 The Additive EuroSCORE

Applications of Risk Scores

Risk models are used for four main purposes: (1) to predict risk for individual patients; (2) to evaluate care over time within an institution; (3) to compare care among institutions; (4) to compare care among surgeons.

It is important to appreciate an essential limitation in applying risk scores to individuals. For a dichotomous variable such as mortality, the observed outcome (died or survived) never matches the predicted outcome (e.g., 10% mortality risk) on an individual level (i.e., individuals cannot be 10% dead!). Thus, a risk model may correctly identify that 10 out of 100 patients with a given set of risk factors may die, but not which 10. Also, because mortality predictions are risk estimates, some authors have suggested that mortality-risk predictions for individual patients should be accompanied by confidence limits, indicating their uncertainty.^5,19 However, currently used risk models do not routinely provide these confidence limits. Furthermore, other authors have questioned the benefit of confidence limits because by not correcting for random or systematic errors, they do not cover the total uncertainty of the measurement.²⁰

Stay updated, free articles. Join our Telegram channel

Join