The current paradigm of primary prevention in cardiology uses traditional risk factors to estimate future cardiovascular risk. These risk estimates are based on prediction models derived from prospective cohort studies and are incorporated into guideline-based initiation algorithms for commonly used preventive pharmacologic treatments, such as aspirin and statins. However, risk estimates are more accurate for populations of similar patients than they are for any individual patient. It may be hazardous to presume that the point estimate of risk derived from a population model represents the most accurate estimate for a given patient. In this review, we exploit principles derived from physics as a metaphor for the distinction between predictions regarding populations versus patients. We identify the following: (1) predictions of risk are accurate at the level of populations but do not translate directly to patients, (2) perfect accuracy of individual risk estimation is unobtainable even with the addition of multiple novel risk factors, and (3) direct measurement of subclinical disease (screening) affords far greater certainty regarding the personalized treatment of patients, whereas risk estimates often remain uncertain for patients. In conclusion, shifting our focus from prediction of events to detection of disease could improve personalized decision-making and outcomes. We also discuss innovative future strategies for risk estimation and treatment allocation in preventive cardiology.
Preventive cardiology guidelines recommend statin treatment allocation based on estimates of cardiac risk using various risk scores. Indeed, 2013 American Heart Association-American College of Cardiology (AHA-ACC) guidelines abandon cholesterol targets altogether and place increased emphasis on risk assessment using a new atherosclerotic cardiovascular disease risk score. Unfortunately, there is an abundance of data demonstrating that our current risk-prediction paradigm often underperforms for given patients, even with the addition of novel risk factors. In this review, we explore possible reasons for this poor performance. In doing so, we make liberal use of analogies and metaphors drawn from the discipline of physics. Although these principles need not be interpreted literally in the clinical context, we believe that they provide an interesting logical framework for our discussion. In addition, we also review alternative strategies for estimating risk and allocating treatment in preventive cardiology.
Problems With the Current Paradigm of Risk Prediction in Preventive Cardiology
The person-population divide
Perhaps the most obvious problem with our current paradigm is the application of population-based risk estimation to individual patients. This brings the dichotomy between the person and the population into sharp focus. In particular, risk scores only provide accurate risk estimates on average and have high intrinsic variance for the prediction of cardiac risk when applied to a given patient. Although this divide is well recognized in the literature, it is often ignored in clinical practice. Thus, it is imperative that physicians understand this limitation when making treatment decisions.
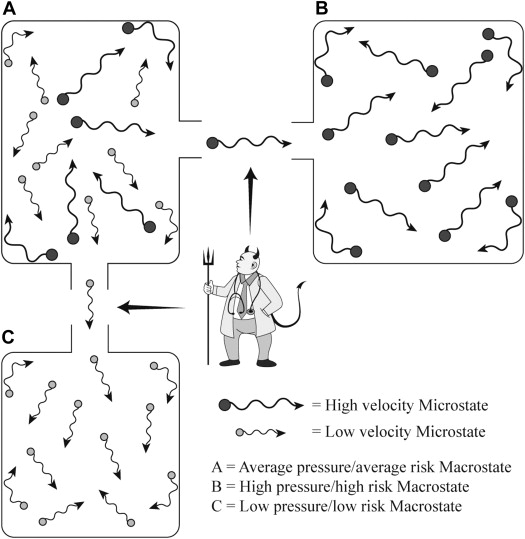
This person-population divide draws interesting comparisons with important phenomena described in other fields of science. In particular, the difference between risk in a person and risk for a population is analogous to a well-known phenomenon described by the kinetic theory of an ideal-gas. The behavior of an individual molecule of gas is unpredictable (as often with risk for an individual patient). In contrast, the behavior of the entire population of gas molecules is highly predictable through the probabilistic ideal-gas laws derived from statistical mechanics. Nevertheless, emergent qualities of the population (such as the temperature and pressure for gas) have no meaning when applied to an individual molecule. Although patients are clearly not molecules, this analogy helps explain why risk in populations and individuals cannot be described in the same way. The properties of one do not necessarily translate to the other, and risk estimates may have limited meaning for any given patient. This fundamental limitation also has broad ramifications for risk prediction models used elsewhere in medicine.
The underlying reason for this person-population divide is both complex and incompletely understood. The combination of stochastic effects and incomplete knowledge of causal factors included in our statistical models may contribute to residual error. However, the previously mentioned kinetic theory metaphor also reminds us that the application of population-based risk estimates to the subsequent prediction of patient risk may represent a form of ecologic fallacy (where inferences for patients are assumed based on inferences derived from the population to whom those patients belong). Risk is a group phenomenon, a population-level measure.
Thus, our ability to directly apply knowledge derived from populations to patient-treatment decisions in preventive cardiology is limited. Admittedly, the degree to which this is a problem depends on the context. For example, public health experts will justifiably argue that these risk prediction methods work well because accurate risk estimates at the level of the population should lead to effective treatment allocation at the level of the population. However, a given doctor facing an individual patient will never be certain that treatment decisions made using risk-model estimates will be accurate for that patient. This is a key problem with over-reliance on current guidelines.
Striving to achieve perfection
Aspiring to near-perfect accuracy in our current risk estimates is a lofty goal. Nonetheless, this aspiration is justified because we often allocate life-long treatments solely based on these estimates (e.g., current guidelines recommend statin therapy for most patients with 10-year atherosclerotic cardiovascular disease risk ≥7.5% ). Thus, the overriding focus of research in preventive cardiology has been on the search of “novel” risk factors that may more accurately classify patients based on risk estimates ( Table 1 ). A myriad of studies have added serologic (e.g., high-sensitivity C-reactive protein), genetic, and imaging (e.g., coronary artery calcium [CAC]) risk factors to improve the accuracy of the newly augmented prediction model.
| High sensitivity troponin |
| High sensitivity C-reactive protein |
| N-terminus pro-brain natriuretic peptide |
| Apolipoproteins (e.g., Apo-B) |
| Lipoprotein “little” a |
| Lipoprotein-associated phospholipase A 2 |
| Genetic polymorphisms (e.g., chromosome 9p21) |
| Carotid intima-media thickness |
| Ankle-brachial index |
| Coronary artery calcium |
∗ This list is not exhaustive; for a more detailed list, see the study by Brotman et al .
There is no doubt that this research has significant merit, as it is an important mechanism for the identification of new risk factors, which may lead to new therapeutic targets. In addition, the presumed intent of most investigators is to merely improve our estimates, not to achieve perfect estimates. However, it can also be argued that iteratively attempting to improve on previous improvements is self-similar to pursuing perfection. Thus, the ultimate, although often subliminal, logical goal of this enterprise is to achieve perfect or near-perfect calibration and discrimination in our risk predictions. The question is whether or not this is actually possible.
Most studies focus on discrimination by reporting the c-index, which can vary from 0.5 (no ability to discriminate) to 1.0 (perfect discrimination). Typical values based on traditional risk factor-based prediction of coronary heart disease (e.g., using the Framingham risk score [FRS]) are in the 0.60 to 0.70 range, depending on the population under study. However, even with the addition of the most powerful novel risk factors, the c-index for well-calibrated cardiac events rarely increases beyond 0.80.
Why cannot we improve risk estimation further? To begin with, there is an upper limit as to how well a “perfectly calibrated” model (important for reporting patient risk estimates) can discriminate (0.83). In addition, models may not translate well across populations and across time periods (because of temporal changes in exposure to risk factors and confounding). Our knowledge of cardiac risk factors also remains incomplete. However, although it is possible that we may one day be able to understand and measure all the factors contributing to a given clinical event, it is clear that mechanistic pathways of disease will become increasingly complex. Thus, although current uncertainty in risk estimates is likely driven most by unknown factors, it is also possible that uncertainty in known factors may become a consideration in the future.
We recognize that there are profound differences between clinical events and phenomena in the realm of quantum physics. However, this issue of uncertainty also draws comparison with another analogy from physics, the “Uncertainty Principle,” described in 1927 by Werner Heisenberg. This principle states that the position and momentum of a particle at any instant cannot be known with complete precision. For example, the more accurately the position of a particle is measured, the less accurately its momentum can be determined. However, perhaps more relevant to the domain of risk prediction, this uncertainty also holds true for energy and time (time is to position as energy is to momentum). Specifically, Energy = 1/2 mv 2 , where mass (m) can be considered analogous to the number of patients in a population and velocity (v) analogous to the average risk in the population (the rate of change over time).
Although quantum uncertainty rarely causes any real problems in clinical practice, the Uncertainty Principle is, nonetheless, clinically important. In particular, it has profound epistemologic implications for deterministic interpretations of risk. If we cannot precisely know every input into a system, especially as these systems become more complex and minute, the fundamental concept of a “Clockwork Universe” is no longer valid. Accordingly, “perfect accuracy” of risk is both logically flawed and operatively unattainable, and we can never eliminate uncertainty altogether. Thus, if risk estimates will continue to demonstrate high uncertainty for patients, should we continue to routinely use them to allocate effective lifelong preventive therapies? Or are alternative strategies that reduce patient uncertainty also worth considering?
Allocating preventive treatment by estimating events in the future versus screening for disease now
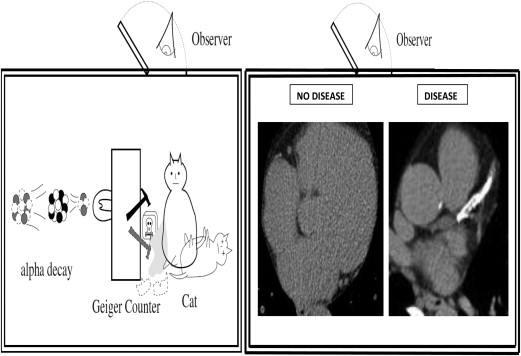
Could screening (measurement for the presence of subclinical disease) represent a more definitive way to personalize preventive treatment than the use of risk estimates for future events? This remains an important outstanding question in preventive cardiology, particularly given the previously mentioned concerns regarding the inherent uncertainty associated with contingent risk estimates at the level of the individual patient. Once again, another concept from physics, “Quantum Superposition,” may be a useful metaphor when considering this issue further. Quantum Superposition holds that objects exist partly in all theoretically possible states simultaneously until measured. For example, light exists as both a wave and particle. The quantum wave function describes this duality in terms of probabilities. When light is measured, the wave-function is collapsed, yielding a result corresponding to only one of the possible configurations (wave or particle) depending on the form of measurement.
By analogy, a patient, at least theoretically, has both disease and no disease until the act of measurement. More simply speaking, it is often clinically justified to treat a patient as if they had disease or as if they did not have disease (traditionally depending on risk estimates). However, once the presence or absence of disease is established (based on screening), only 1 of these 2 choices is proved correct. It is the act of the measurement itself that collapses the probability function for the patient and reveals the underlying diagnostic state. This may have important connotations for personalized treatment decisions. Quantum Superposition argues that basing patient treatment decisions (e.g., allocating preventive statins) on contingencies (risk estimates) that are inherently uncertain for patients may be a less effective personalized strategy than the allocation of treatment based on measurement of disease in that patient. Although we can never collapse the risk (probability) distribution for future cardiac events in each patient, the act of screening can collapse the probability distribution of disease in each patient. In this way, screening affords far superior patient certainty about the presence of disease than risk scores afford patient certainty about future events. By shifting our common focus from events in the future to the presence or absence of disease in the present, the preventive cardiology community could improve the certainty on which we base our personalized treatment decisions.
Nowhere is this better illustrated than the example of Schrödinger’s famous cat ( Figure 1 ). Like Schrödinger’s cat, one way we can increase the certainty of our preventive treatment decisions is to look inside the “box” to see whether disease is present or absent. Although current coronary artery screening (CAD) screening modalities do not themselves afford perfect accuracy for the detection of atherosclerosis and their use in a therapeutic decision algorithms needs to be tested in prospective randomized studies, it is important to reiterate that using risk estimates to allocate preventive cardiac treatments has never been formally tested either.
Another potential problem with allocating treatments based on traditional cardiac risk-prediction models is that these models incorporate variables that were derived based on their association with cardiac events, rather than the underlying disease (atherosclerosis). Although subtle, this approach inherently distinguishes between prognosis (estimating events) and diagnosis (measuring presence of disease by screening). Admittedly, early cardiovascular epidemiology pioneers constructed this event-based method within the limits of the technology of their day. This was the era of “black-box” epidemiology (making causal inferences on the basis of statistical findings, without worrying about the mechanisms that might underlie them).
Thus, the “inputs” into our current risk-prediction models are by convention risk factors for events, not for the presence of disease. Although most event risk factors are also causally important in the development of disease, this is not necessarily the case. This distinction is therapeutically important because, with few exceptions, without the disease (e.g., atherosclerosis), one cannot have the related event (e.g., myocardial infarction)—irrespective of risk factor burden. For example, elderly patients (>75 years) without evidence of CAD have lower event rates than younger patients (<45 years) with high burdens of CAD. As a consequence, although imaging-based metrics (like CAC) have been interpreted as “risk factors” for cardiac events, given that they are actual measures of the disease (atherosclerosis) causing these events, they may be best interpreted as distinct from traditional risk factors.
The use of traditional event risk factors that are not causally linked to either the disease pathogenesis or the mechanisms of action of treatment may have important implications for the allocation of such treatment. For example, current prevention guidelines recommend that statin therapy be initiated based on traditional risk estimates (e.g., for those with a 2013 AHA-ACC atherosclerotic cardiovascular disease risk score of >7.5%), although there remains no randomized-trial evidence supporting statin administration based on risk estimates that are heavily influenced by nonlipid factors (the main causal pathway by which statins act), such as age and gender. In contrast, screening for cardiac disease could focus on statin therapy on patients who actually have evidence for disease and who may benefit from the plaque delipidation and stabilization properties of statins.
Implications for Future Research
We believe that the previously mentioned issues have important clinical implications for preventive cardiology. In particular, they call into question the paradigm of using population-based risk estimates for the allocation of treatment in a given patient (despite the inclusion of novel risk markers). Indeed, using risk prediction algorithms to bridge the divide between epidemiologic risk (the population) and clinical treatment (the patient), preventive cardiologists have been recapitulating the efforts of Maxwell’s Demon ( Figure 2 ). James Clerk Maxwell introduced his demon in a thought experiment designed to raise questions about the second law of thermodynamics, a concept relating to the aforementioned kinetic theory of gas (Maxwell J.C. Theory of Heat , Longmans, London, 1871),
“… if we conceive of a being whose faculties are so sharpened that he can follow every molecule in its course, such a being, whose attributes are as essentially finite as our own, would be able to do what is impossible to us. For we have seen that molecules in a vessel full of air at uniform temperature are moving with velocities by no means uniform, though the mean velocity of any great number of them, arbitrarily selected, is almost exactly uniform. Now let us suppose that such a vessel is divided into two portions, A and B, by a division in which there is a small hole, and that a being, who can see the individual molecules, opens and closes this hole, so as to allow only the swifter molecules to pass from A to B, and only the slower molecules to pass from B to A. He will thus, without expenditure of work, raise the temperature of B and lower that of A, in contradiction to the second law of thermodynamics.”