Fig. 12.1
Illustration of the effect of system latency on the target localization accuracy (from Sharp et al. [13])
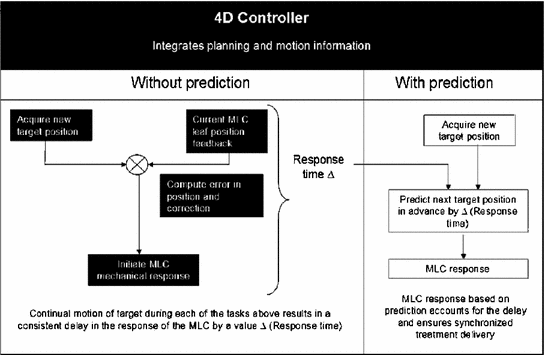
Fig. 12.2
Necessity for predicting respiratory motion, illustrated in the framework of a MLC based linear accelerator design (from Vedam et al. [15])
Predicting the position of the target in advance is therefore considered as an approach to minimize positioning errors due to the lag in system response. The ultimate goal of prediction is to ensure that the radiation beam encompasses the target as it moves throughout the respiratory cycle. Figure 12.2 illustrates the necessity for predicting respiratory motion within the framework of an MLC based gantry mounted linear accelerator design.
12.2 Understanding Respiratory Motion Prediction
Respiratory motion in radiation therapy is typically monitored through mainly two approaches: (a) Direct tumor tracking or (b) Indirect tumor surrogate tracking. Direct tumor tracking is usually implemented through on board imaging systems that track the position of the tumor through radiographic/fluoroscopic imaging or electromagnetic transponder tracking. Such approaches, more often than not, involve implantation of fiducials into or in the vicinity of the tumor volume. Indirect tumor surrogate tracking involves monitoring the position of internal or external anatomy based surrogates that have an established position correlation with respect to the actual tumor motion throughout the respiratory cycle. An example of an external surrogate is chest/abdominal wall motion. The lung/diaphragm interface is considered a good internal surrogate for certain thoracic and abdominal tumors. All of the above approaches provide the input data necessary for predicting respiratory motion.
In order to understand the concepts behind respiratory motion prediction, it is useful to introduce and define some basic terminology. The following terms represent the various parameters that will find mention in all of the predictive models that will be discussed henceforth.
12.2.1 Sampling Rate
Sampling rate refers to the frequency at which respiratory motion data is sensed or acquired. It is usually quantified in terms of samples/sec or Hz. Faster sampling rates result in greater resolution of respiratory motion, thereby inspiring higher confidence in the accuracy/precision of respiratory motion monitoring. Direct tumor tracking, being a typically resource intensive process yields slower sampling rates (of the order of 10 samples/sec) as compared to indirect tumor surrogate tracking, which can yield near real time (30 samples/sec) sampling rates.
12.2.2 Latency
Adaptive systems require a finite amount of time to sense and react to changes in the sensed parameter, which presently, is respiratory motion. Such a time interval is usually indicative of the lag in the response of the system to the change in respiratory tumor position, and is therefore defined as latency. It is usually quantified in milliseconds or seconds.
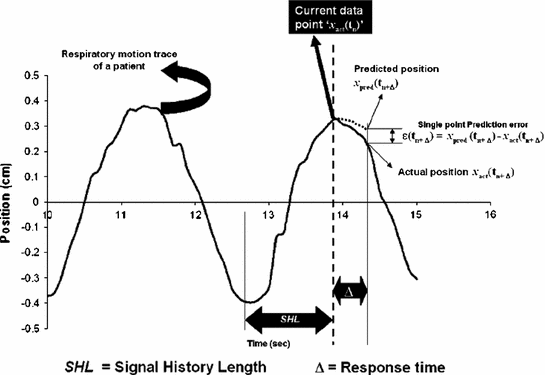

Fig. 12.3
Illustration of the prediction parameters, signal history length and response time relative to the current data point in the respiratory motion trace (from Vedam et al. [15])
12.2.3 Signal History/Training Length
Predicting respiratory tumor position at a future time instant is always based on respiratory motion information collected from the past. The duration of such past motion history used for prediction is referred to as signal history length or training length. It is usually quantified in milliseconds or seconds.
12.2.4 Response Time
The time interval in advance for which the prediction of respiratory tumor position is made is referred to as response time. It is usually quantified in milliseconds.
Figure 12.3 provides an illustration of the above parameters in the context of respiratory motion prediction.
12.3 Respiratory Motion Prediction Models
In increasing order of complexity, predictive filter algorithms span the range from the simpler stationary linear filter models to the highly complex adaptive nonlinear filter models [15]. Several predictive models have been studied recently for the purpose of image guided and adaptive radiotherapy. The following sections provide a brief insight into some of these predictive models.
For any given random sequence 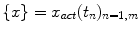 at a given time instant
at a given time instant 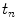 , prediction provides an estimate
, prediction provides an estimate 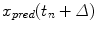 of
of 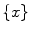 , ahead by an interval
, ahead by an interval 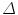 . The prediction
. The prediction 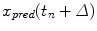 is based on a number of previous values of the sequence, referred to as signal history window; the length of which is referred to as signal history length SHL, as seen in the equation below:
is based on a number of previous values of the sequence, referred to as signal history window; the length of which is referred to as signal history length SHL, as seen in the equation below:
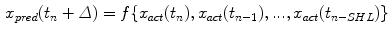
Depending on how one employs the chosen signal history for prediction, several different approaches are available to obtain the predicted position at a time instance in the future.
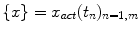 at a given time instant
at a given time instant 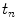 , prediction provides an estimate
, prediction provides an estimate 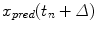 of
of 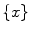 , ahead by an interval
, ahead by an interval 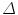 . The prediction
. The prediction 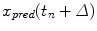 is based on a number of previous values of the sequence, referred to as signal history window; the length of which is referred to as signal history length SHL, as seen in the equation below:
is based on a number of previous values of the sequence, referred to as signal history window; the length of which is referred to as signal history length SHL, as seen in the equation below: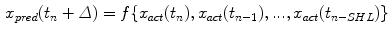
(12.1)
12.3.1 Parametric Models
If one makes assumptions about the functional form of the respiratory signal, these functions can be used to guide a prediction algorithm. This approach has been studied by Vedam et al. [15]; employing a sinusoidal model to predict external chest wall position. They found that the sinusoidal model did reduce the geometric error introduced by the response time compared with no prediction; adaptive prediction models performed better in reducing the geometric uncertainty.
12.3.2 Empirical Algorithms
In this approach, the prediction is based on a combination (linear/non linear) of prior inputs from some past history of the respiratory motion signal, as shown below:
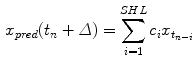
where 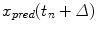 is the predicted position in advance by a time
is the predicted position in advance by a time 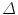 , {c} is the vector of filter coefficients and
, {c} is the vector of filter coefficients and 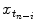 represents a vector of past respiratory motion signal inputs. In such a formulation, the problem of optimal prediction is essentially a problem of optimization of the filter coefficient vector {c}. For stationary input signals with known statistics, the optimal {c} values are given by the Yule-Walker equations [1], or a least mean squares algorithm approach, resulting in what is referred to as linear filtering/prediction.
represents a vector of past respiratory motion signal inputs. In such a formulation, the problem of optimal prediction is essentially a problem of optimization of the filter coefficient vector {c}. For stationary input signals with known statistics, the optimal {c} values are given by the Yule-Walker equations [1], or a least mean squares algorithm approach, resulting in what is referred to as linear filtering/prediction.
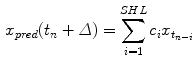
(12.2)
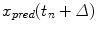 is the predicted position in advance by a time
is the predicted position in advance by a time 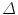 , {c} is the vector of filter coefficients and
, {c} is the vector of filter coefficients and 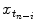 represents a vector of past respiratory motion signal inputs. In such a formulation, the problem of optimal prediction is essentially a problem of optimization of the filter coefficient vector {c}. For stationary input signals with known statistics, the optimal {c} values are given by the Yule-Walker equations [1], or a least mean squares algorithm approach, resulting in what is referred to as linear filtering/prediction.
represents a vector of past respiratory motion signal inputs. In such a formulation, the problem of optimal prediction is essentially a problem of optimization of the filter coefficient vector {c}. For stationary input signals with known statistics, the optimal {c} values are given by the Yule-Walker equations [1], or a least mean squares algorithm approach, resulting in what is referred to as linear filtering/prediction.In the case of real-time respiratory motion, such statistics may not be completely available. Therefore, linear adaptive filtering is employed for determining optimal values of {c}, which are further used for prediction, according to Eq. (12.2). In adaptive filtering, coefficient vector {c} is updated after each prediction 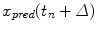 through a correction term that is proportional to the prediction error
through a correction term that is proportional to the prediction error 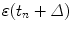 of the most recent prediction, thereby introducing a feedback that attempts to minimize prediction error
of the most recent prediction, thereby introducing a feedback that attempts to minimize prediction error 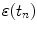 . Linear prediction and adaptive linear prediction methods have been studied by Sharp et al. [13], Vedam et al. [15] and Murphy et al. [5].
. Linear prediction and adaptive linear prediction methods have been studied by Sharp et al. [13], Vedam et al. [15] and Murphy et al. [5].
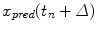 through a correction term that is proportional to the prediction error
through a correction term that is proportional to the prediction error 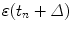 of the most recent prediction, thereby introducing a feedback that attempts to minimize prediction error
of the most recent prediction, thereby introducing a feedback that attempts to minimize prediction error 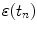 . Linear prediction and adaptive linear prediction methods have been studied by Sharp et al. [13], Vedam et al. [15] and Murphy et al. [5].
. Linear prediction and adaptive linear prediction methods have been studied by Sharp et al. [13], Vedam et al. [15] and Murphy et al. [5].Other increasingly complex approaches to empirical algorithms have been examined. McCall et al. [4], have employed a dual component model to separate the respiratory motion pattern into periodic and non periodic components. The periodic component is usually a representative mean respiratory motion trace, estimated from a set of recent respiratory motion data. The non periodic component, which is the difference in between the respiratory signal and the magnitude of its corresponding periodic component, is described as an auto regressive moving average (ARMA) model. Ren et al. [8], have also employed a variation of the above ARMA model to predict respiratory motion. To account for instability inherent in respiratory motion patterns, they have employed an iterative least mean squares approach to adapt the ARMA coefficients in order to minimize prediction errors.
Ruan et al. [10], have reported on a comprehensive approach to respiratory motion prediction based on local regression models. Their approach addresses the problem in three stages. These include (a) capturing representative system dynamics or determine a representative state of a portion of the input respiratory motion data, (b) developing a local regression based training model to train the predictor from previous observations of respiratory motion and (c) iteratively adjusting the weights of coefficients in the training model to incorporate any residual fading temporal correlations.
< div class='tao-gold-member'>
Only gold members can continue reading. Log In or Register to continue
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


