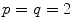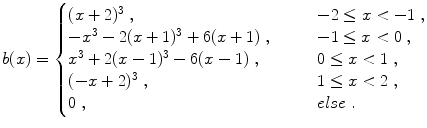, Xiaoyi Jiang1, Mohammad Dawood2 and Klaus P. Schäfers2
(1)
Department of Mathematics and Computer Science, University of Münster, Münster, Germany
(2)
European Institute for Molecular Imaging, University of Münster, Münster, Germany
In the introduction of this book we have seen that PET image acquisition is susceptible to motion artifacts. The first step to overcome this problem is the separation of the measured data into different motion states via gating as described in Sect. 1.3. The next step is the estimation of motion between these gated reconstructions. This step is crucial as its accuracy highly influences the quality of the final motion corrected image.
In this chapter we discuss different algorithmic paradigms in terms of image registration and optical flow for motion estimation. For both paradigms, a focus is laid on the preservation of radioactivity (mass-preservation) to incorporate a priori information. For image registration, different data terms are introduced which are suitable for monomodal PET registration in combination with mass-preservation. In particular, a data term adopted to noisy PET data is proposed with the SAD measure. The preservation of mass requires diffeomorphic transformations to be a valid assumption. Thus, different regularization schemes will be introduced and discussed. In addition to the non-parametric transformation model we also present motion estimation using the popular parametric transformation model based on B-splines for image registration. For optical flow, classical local and global approaches are introduced and advanced methods are briefly discussed. In particular, mass-preserving optical flow in combination with non-quadratic penalization is addressed. The last part of this chapter compares the two algorithmic paradigms and intends to provide some guidance to finding an appropriate method for motion estimation and its configuration in practice.
2.1 Image Registration
Image registration is a versatile approach to motion estimation and provides a full range of application-specific options. We give an introduction to image registration including suitable options for the data term in Sect. 2.1.1 and the regularization functional in Sect. 2.1.2. The alternative to non-parametric image registration in terms of B-spline transformations is discussed in Sect. 2.1.3. One of the main messages of this book is the mass-preserving transformation model introduced in Sect. 2.1.4 which is tailored for gated PET. We refer to the comprehensive reviews of image registration for further reading [18, 49, 63, 66, 88, 90, 94, 95, 139].
The aim of image registration is to spatially align two corresponding images. In order to formulate this definition of image registration mathematically, we need to find a way to measure the similarity of two images. The objective is then to find a meaningful spatial transformation that, applied to one of the images, maximizes the similarity.
For motion estimation, a so-called template image 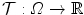 is registered onto a reference image
is registered onto a reference image 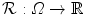 , where
, where 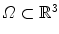 is the image domain. This yields a spatial transformation
is the image domain. This yields a spatial transformation 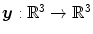 representing point-to-point correspondences between
representing point-to-point correspondences between 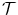 and
and 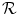 . To find
. To find 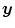 , the following functional has to be minimized
, the following functional has to be minimized
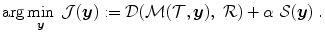
Here 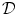 denotes the distance functional measuring the dissimilarity between the transformed template image and the fixed reference image.
denotes the distance functional measuring the dissimilarity between the transformed template image and the fixed reference image. 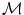 is the transformation model specifying how the transformation
is the transformation model specifying how the transformation 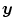 should be applied to the template image
should be applied to the template image 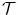 .
. 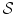 is the regularization functional which penalizes non-smooth transformations and thus enforces meaningful solutions.
is the regularization functional which penalizes non-smooth transformations and thus enforces meaningful solutions.
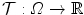 is registered onto a reference image
is registered onto a reference image 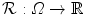 , where
, where 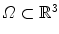 is the image domain. This yields a spatial transformation
is the image domain. This yields a spatial transformation 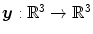 representing point-to-point correspondences between
representing point-to-point correspondences between 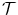 and
and 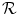 . To find
. To find 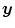 , the following functional has to be minimized
, the following functional has to be minimized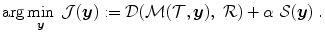
(2.1)
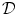 denotes the distance functional measuring the dissimilarity between the transformed template image and the fixed reference image.
denotes the distance functional measuring the dissimilarity between the transformed template image and the fixed reference image. 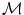 is the transformation model specifying how the transformation
is the transformation model specifying how the transformation 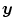 should be applied to the template image
should be applied to the template image 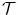 .
. 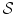 is the regularization functional which penalizes non-smooth transformations and thus enforces meaningful solutions.
is the regularization functional which penalizes non-smooth transformations and thus enforces meaningful solutions.The standard transformation model is simply given by an interpolation of 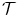 at the transformed grid
at the transformed grid 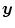
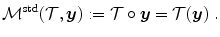
We will discuss an alternative transformation model for mass-preserving image registration in Definition 2.11. A discussion of different options for the data term 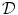 is given in the next Sect. 2.1.1 and for the regularization term
is given in the next Sect. 2.1.1 and for the regularization term 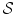 in Sect. 2.1.2.
in Sect. 2.1.2.
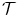 at the transformed grid
at the transformed grid 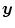
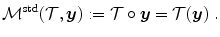
(2.2)
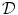 is given in the next Sect. 2.1.1 and for the regularization term
is given in the next Sect. 2.1.1 and for the regularization term 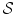 in Sect. 2.1.2.
in Sect. 2.1.2.2.1.1 Data Terms
The data term measures the dissimilarity, i.e., reversal of the similarity, of two input images. In Eq. (2.1) the transformed template image is compared to the reference image. For simplicity we will use the original template image (without transformation) for the following definitions without loss of generality.
(Dis)similarity measures for monomodal registration tasks are best suited for motion correction of gated PET data. We thus restrict the discussion in the rest of this section to these monomodal measures. For a more detailed discussion of similarity measures for multimodal studies, such as mutual information (which measures the amount of shared information of two images) or normalized gradient fields (which measures deviations in the gradients of the input images), we refer to [95].
A common dissimilarity measure for monomodal image registration is 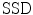 , which is introduced in the following Definition. Differences of the reference and the template image are measured quadratically.
, which is introduced in the following Definition. Differences of the reference and the template image are measured quadratically.
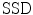 , which is introduced in the following Definition. Differences of the reference and the template image are measured quadratically.
, which is introduced in the following Definition. Differences of the reference and the template image are measured quadratically.Definition 2.1 (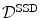 – Sum of squared differences).
– Sum of squared differences).
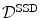 – Sum of squared differences).
– Sum of squared differences).The sum of squared differences (SSD) of two images 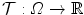 and
and 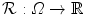 on a domain
on a domain 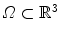 is defined as
is defined as
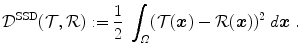
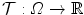 and
and 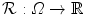 on a domain
on a domain 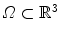 is defined as
is defined as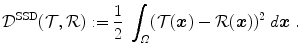
(2.3)
SSD measures the point-wise distances of image intensities. For images with locally similar intensities the measure gets low. SSD has to be minimized and has its optimal value at 0.
Large differences in the input images are often induced by noise which consequently leads to a high energy in the data term. L1-like distance measures are often used in optical flow techniques [19] to overcome this problem. The L1 distance of two images 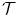 and
and 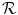 is defined as
is defined as
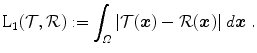
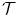 and
and 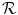 is defined as
is defined as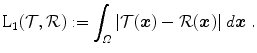
(2.4)
Using this functional as a data term in Eq. (2.1) raises problems as we require differentiability of all components during optimization. As the absolute value function is not differentiable at zero, the idea is thus to create a differentiable version of the L1 distance by adding a differentiable outer function ψ to the difference in Eq. (2.4) with a similar behavior to the absolute value function.
Definition 2.2 (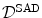 – Sum of absolute differences).
– Sum of absolute differences).
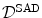 – Sum of absolute differences).
– Sum of absolute differences).The (approximated) sum of absolute differences (SAD) of two images 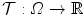 and
and 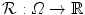 on a domain
on a domain 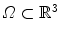 is defined as
is defined as
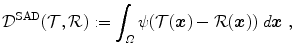
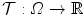 and
and 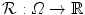 on a domain
on a domain 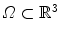 is defined as
is defined as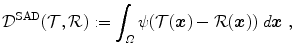
(2.5)
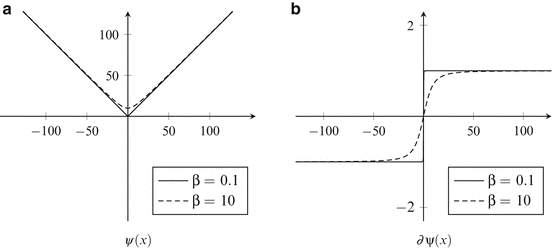
where 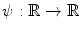 is the continuously differentiable Charbonnier penalizing function [28] with a small positive constant
is the continuously differentiable Charbonnier penalizing function [28] with a small positive constant 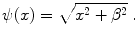
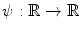 is the continuously differentiable Charbonnier penalizing function [28] with a small positive constant
is the continuously differentiable Charbonnier penalizing function [28] with a small positive constant 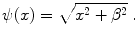
(2.6)
Remark 2.2.
The function ψ in Eq. (2.6) is always greater than zero. Consequently, 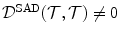 . This issue could be fixed by subtracting β
. This issue could be fixed by subtracting β
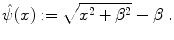
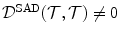 . This issue could be fixed by subtracting β
. This issue could be fixed by subtracting β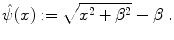
(2.7)
For minimization of the registration functional we need to compute the derivatives of the functional and hence the first
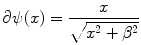
and second derivative of ψ
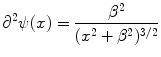
are given here for completeness.
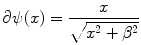
(2.8)
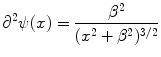
(2.9)
The behavior of the penalizing function ψ for different values of β is shown in Fig. 2.1. It can be observed that ψ becomes more quadratic around zero for higher β values. This might prevent abrupt jumps in the first derivative between − 1 and 1 during optimization, thus stabilizing the optimization process.
2.1.2 Regularization
According to Hadamard [61] a problem is called well-posed if there
1.
Exists a solution that is
2.
Unique and when
3.
Small changes in data lead only to small changes in the result.
In image registration, small changes in the data can lead to large changes in the results. Further, as the uniqueness is generally not given, image registration is ill-posed [48]. This makes regularization inevitable and essential to find feasible transformations.
Regularization restricts the space of possible transformations to a smaller set of reasonable functions. Regularization should be chosen depending on the application and can either be implicit or explicit. If the transformation is regularized by the properties of the space itself, as in parametric image registration, we speak of implicit regularization. For example, for a rigid 3D transformation only a total of three rotation and three translation parameters need to be estimated instead of a 3D motion vector for each voxel. In explicit regularization, a penalty is added to the registration functional to avoid non-smooth transformations. The penalty is often based on a model that is physically sound and fits the processed data.
As the regularization for parametric transformations is implicitly given we will only analyze penalties for non-linear image registration in this section. In the rest of this section we will introduce the following regularizers:
These regularizers are specifically chosen as diffusion regularization is typically used for optical flow applications. Further, Vampire relies on hyperelastic regularization, which is a non-linear generalization of linear elastic regularization. More information about regularization (e.g., curvature or log-elasticity) and additional constraints, which are beyond the scope of this book, can be found in [3, 48, 94, 99, 107].
Hereinafter, we assume a given transformation 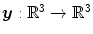 which is composed of the spatial position
which is composed of the spatial position 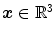 and a deformation (or displacement)
and a deformation (or displacement) 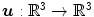 at position
at position 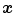 , i.e.,
, i.e., 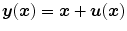 .
.
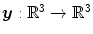 which is composed of the spatial position
which is composed of the spatial position 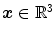 and a deformation (or displacement)
and a deformation (or displacement) 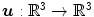 at position
at position 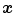 , i.e.,
, i.e., 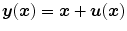 .
.2.1.2.1 Diffusion Regularization
One of the simplest ways to control the behavior of the transformation is diffusion regularization [47]. The basic idea is to disallow large variations in the gradient of the motion vector between neighboring voxels, i.e., oscillations in the deformation 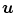 are penalized.
are penalized.
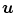 are penalized.
are penalized.The motivation is thus simply a demanded smoothness of the transformation and no physical one. An advantage of diffusion regularization over other methods is its low computational complexity which allows fast computations and the treatment of high-dimensional data [94]. This becomes important when striving for real-time computations, which is why diffusion regularization is popular for optical flow techniques, cf. Sect. 2.2.
Definition 2.3 (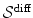 – Diffusion regularization).
– Diffusion regularization).
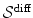 – Diffusion regularization).
– Diffusion regularization).For a transformation 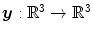 with
with 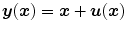 and
and 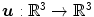 , the diffusion regularization energy is defined as
, the diffusion regularization energy is defined as
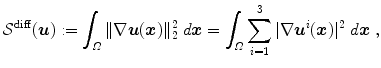
where the (squared) Frobenius norm is defined as 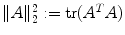 for matrices
for matrices  .
. 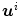 denotes the i-th component of
denotes the i-th component of 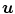 with i ∈ { 1, 2, 3}.
with i ∈ { 1, 2, 3}.
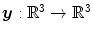 with
with 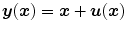 and
and 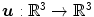 , the diffusion regularization energy is defined as
, the diffusion regularization energy is defined as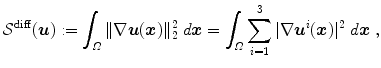
(2.10)
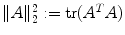 for matrices
for matrices  .
. 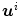 denotes the i-th component of
denotes the i-th component of 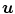 with i ∈ { 1, 2, 3}.
with i ∈ { 1, 2, 3}.2.1.2.2 Elastic Regularization
As indicated in the introduction of this section, regularization methods can be motivated physically. This is the case for linear elastic regularization which measures the forces of a transformation applied to an elastic material [17] (Lagrange frame). In the language of elasticity we would say that the stress due to strain is measured. Or vice versa, in a more physical motivation, the deformation (strain) is a reaction of force (stress) [94] (Euler frame).
Definition 2.4 (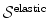 – Elastic regularization).
– Elastic regularization).
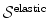 – Elastic regularization).
– Elastic regularization).For a transformation 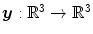 with
with 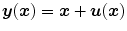 and
and 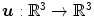 , the elastic regularization energy is defined as
, the elastic regularization energy is defined as
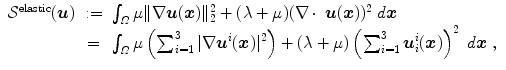
where ![$$\mu \in \mathbb{R}^{>0}$$
” src=”/wp-content/uploads/2016/09/A319392_1_En_2_Chapter_IEq49.gif”></SPAN> and <SPAN id=IEq50 class=InlineEquation><IMG alt=]() 0}$$
” src=”/wp-content/uploads/2016/09/A319392_1_En_2_Chapter_IEq50.gif”> are the Lamé constants according to Ciarlet [30]. Again,
0}$$
” src=”/wp-content/uploads/2016/09/A319392_1_En_2_Chapter_IEq50.gif”> are the Lamé constants according to Ciarlet [30]. Again, 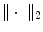 is the Frobenius norm (see Eq. (2.10)) and
is the Frobenius norm (see Eq. (2.10)) and 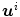 denotes the i-th component of
denotes the i-th component of 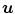 with i ∈ { 1, 2, 3}.
with i ∈ { 1, 2, 3}.
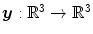 with
with 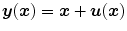 and
and 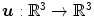 , the elastic regularization energy is defined as
, the elastic regularization energy is defined as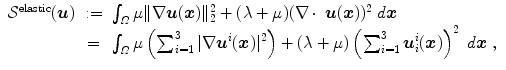
(2.11)
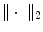 is the Frobenius norm (see Eq. (2.10)) and
is the Frobenius norm (see Eq. (2.10)) and 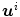 denotes the i-th component of
denotes the i-th component of 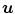 with i ∈ { 1, 2, 3}.
with i ∈ { 1, 2, 3}.To better understand the physical interpretation of the elastic energy we will take a look at some useful properties of elasticity in terms of the Poisson ratio and Young’s modulus.
Definition 2.5 (ν – Poisson ratio).
The Poisson (contraction) ratio is defined as
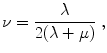
for the Lamé constants ![$$\mu \in \mathbb{R}^{>0}$$
” src=”/wp-content/uploads/2016/09/A319392_1_En_2_Chapter_IEq54.gif”></SPAN> and <SPAN id=IEq55 class=InlineEquation><IMG alt=]() 0}$$
” src=”/wp-content/uploads/2016/09/A319392_1_En_2_Chapter_IEq55.gif”> in Definition 2.4.
0}$$
” src=”/wp-content/uploads/2016/09/A319392_1_En_2_Chapter_IEq55.gif”> in Definition 2.4.
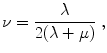
(2.12)
The Poisson ratio ν measures the amount of compression for the linear elastic model. If a material is compressed in one direction, the Poisson ratio measures the quotient of this value and the expansion in the other directions. For compressible materials we thus have a small quotient and for incompressible materials a large one. To model incompressible materials in the registration setting, the Poisson ratio needs to be weighted high. Note that this interpretation only holds for small displacements since we are dealing with a linear model.
Definition 2.6 (E – Young’s modulus).
Young’s modulus is defined as
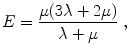
for the Lamé constants ![$$\mu \in \mathbb{R}^{>0}$$
” src=”/wp-content/uploads/2016/09/A319392_1_En_2_Chapter_IEq56.gif”></SPAN> and <SPAN id=IEq57 class=InlineEquation><IMG alt=]() 0}$$
” src=”/wp-content/uploads/2016/09/A319392_1_En_2_Chapter_IEq57.gif”> in Definition 2.4.
0}$$
” src=”/wp-content/uploads/2016/09/A319392_1_En_2_Chapter_IEq57.gif”> in Definition 2.4.
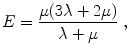
(2.13)
Young’s modulus E is the quotient of stress (tension) and strain (stretch) in the same direction. The connection between the Lamé constants, Poisson ratio, and Young’s modulus is given by
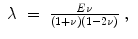
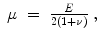
![$$\displaystyle{ T^{d}=\left [\begin{array}{*{10}c} 15.1 &-5.0&-7.2&-0.3& & & & & 0\\ -5.0 & 23.9 &-4.5 &-7.2 &-0.3 & & & & \\ -7.2&-4.5& 24.0 &-4.5&-7.2&-0.3& & &\\ -0.3 &-7.2 &-4.5 & 24.0 &-4.5 &-7.2 &-0.3 && \\ & \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & \ddots &\\ & &-0.3 &-7.2 &-4.5 & 24.0 &-4.5 &-7.2&-0.3 \\ & & &-0.3&-7.2&-4.5& 24.0 &-4.5&-7.2\\ & & & &-0.3 &-7.2 &-4.5 & 23.9 &-5.0 \\ 0 & & & & &-0.3&-7.2&-5.0& 15.1 \end{array} \right ] \in \mathbb{R}^{n^{d},n^{d} } }$$](/wp-content/uploads/2016/09/A319392_1_En_2_Chapter_Equ41.gif)
with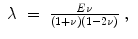
(2.14)
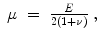
(2.15)
2.1.2.3 Hyperelastic Regularization
In many medical applications of image registration the user has a priori knowledge about the processed data concerning the allowed deformations. For example the invertibility of the transformation is a general requirement. More specific knowledge, like, e.g., the degree of compressibility of tissue can also be controlled. We have seen in the linear elastic case that the Poisson ratio (Definition 2.6) gives a measure for compressibility of small deformations. In the non-linear case, the determinant of the Jacobian of the transformation measures the volume change and can thus be used to control the compression behavior – even for large deformations. This is done with polyconvex hyperelastic regularization [22, 30, 40]. The regularization functional 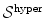 controls changes in length, area of the surface, and volume of
controls changes in length, area of the surface, and volume of 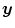 and guarantees thereby in particular the invertibility of the estimated transformation.
and guarantees thereby in particular the invertibility of the estimated transformation.
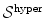 controls changes in length, area of the surface, and volume of
controls changes in length, area of the surface, and volume of 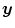 and guarantees thereby in particular the invertibility of the estimated transformation.
and guarantees thereby in particular the invertibility of the estimated transformation.Definition 2.7 (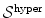 – Hyperelastic regularization).
– Hyperelastic regularization).
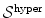 – Hyperelastic regularization).
– Hyperelastic regularization).Let 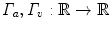 be positive and strictly convex functions, with Γ v satisfying
be positive and strictly convex functions, with Γ v satisfying 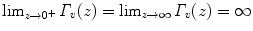 . The hyperelastic regularization energy caused by the transformation
. The hyperelastic regularization energy caused by the transformation 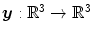 with
with 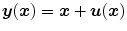 and
and 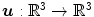 is defined as
is defined as
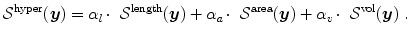
The three summands individually control changes in length, area of the surface, and volume
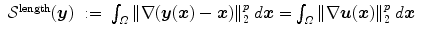
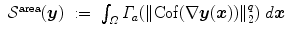
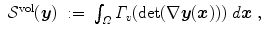
where 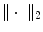 is the Frobenius norm (see Eq. (2.10)) and
is the Frobenius norm (see Eq. (2.10)) and 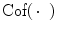 denotes the cofactor matrix.
denotes the cofactor matrix.
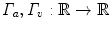 be positive and strictly convex functions, with Γ v satisfying
be positive and strictly convex functions, with Γ v satisfying  . The hyperelastic regularization energy caused by the transformation
. The hyperelastic regularization energy caused by the transformation 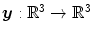 with
with 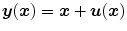 and
and 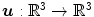 is defined as
is defined as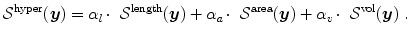
(2.17)
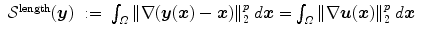
(2.18)
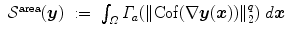
(2.19)
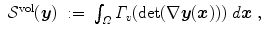
(2.20)
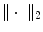 is the Frobenius norm (see Eq. (2.10)) and
is the Frobenius norm (see Eq. (2.10)) and 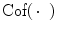 denotes the cofactor matrix.
denotes the cofactor matrix.In the formulation in Eq. (2.1), the positive real number α balances between minimizing the data driven energy term (maximizing the image similarity) and retaining smooth and realistic transformations, which is controlled by the regularization energy. As each term of the hyperelastic regularizer has an individual weighting factor, α can be set to 1 and only α l , α a , and α v need to be determined.
For α v > 0, the conditions for Γ v claimed above ensure 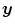 is a diffeomorphism [40]. This allows us to omit the absolute value bars later in Eq. (2.45) of the mass-preserving transformation model. Hyperelastic regularization has the ability of modeling tissue characteristics like compressibility, improves the robustness against noise and thus enforces realistic cardiac and respiratory motion estimates.
is a diffeomorphism [40]. This allows us to omit the absolute value bars later in Eq. (2.45) of the mass-preserving transformation model. Hyperelastic regularization has the ability of modeling tissue characteristics like compressibility, improves the robustness against noise and thus enforces realistic cardiac and respiratory motion estimates.
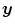 is a diffeomorphism [40]. This allows us to omit the absolute value bars later in Eq. (2.45) of the mass-preserving transformation model. Hyperelastic regularization has the ability of modeling tissue characteristics like compressibility, improves the robustness against noise and thus enforces realistic cardiac and respiratory motion estimates.
is a diffeomorphism [40]. This allows us to omit the absolute value bars later in Eq. (2.45) of the mass-preserving transformation model. Hyperelastic regularization has the ability of modeling tissue characteristics like compressibility, improves the robustness against noise and thus enforces realistic cardiac and respiratory motion estimates.2.1.2.4 Relations
To deepen the understanding of the regularization energies described in this section, we highlight some similarities and differences. This helps us to understand the relations between the different regularization variants. As we will see in Sect. 2.1.4, controlling volume changes plays an important role in connection with the mass-preserving motion estimation approach Vampire. Accordingly, this aspect is highlighted in particular.
Diffusion ↔ Elastic
As we have seen, the elastic energy consists of the two terms 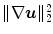 and
and 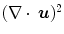 . The interpretation of the latter is revealed as a measure of compressibility, i.e., of volume changes. The first term is the known diffusion regularization term, which is hence integrated into the elastic energy.
. The interpretation of the latter is revealed as a measure of compressibility, i.e., of volume changes. The first term is the known diffusion regularization term, which is hence integrated into the elastic energy.
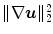 and
and 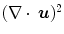 . The interpretation of the latter is revealed as a measure of compressibility, i.e., of volume changes. The first term is the known diffusion regularization term, which is hence integrated into the elastic energy.
. The interpretation of the latter is revealed as a measure of compressibility, i.e., of volume changes. The first term is the known diffusion regularization term, which is hence integrated into the elastic energy.Diffusion ↔ Hyperelastic
Diffusion regularization is included into hyperelastic regularization. The length term 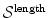 in Eq. 2.17 equals the diffusion regularization term. The hyperelastic regularization energy has two additional energy terms –
in Eq. 2.17 equals the diffusion regularization term. The hyperelastic regularization energy has two additional energy terms – 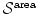 measuring changes in area and
measuring changes in area and 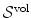 measuring changes in volume.
measuring changes in volume.
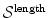 in Eq. 2.17 equals the diffusion regularization term. The hyperelastic regularization energy has two additional energy terms –
in Eq. 2.17 equals the diffusion regularization term. The hyperelastic regularization energy has two additional energy terms – 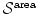 measuring changes in area and
measuring changes in area and 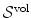 measuring changes in volume.
measuring changes in volume.Elastic ↔ Hyperelastic
The Jacobian determinant 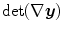 represents the exact volume change due to a transformation
represents the exact volume change due to a transformation 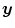 . Consequently, a value of one characterizes incompressibility. Let us recall, the Poisson ratio ν in the linear elastic model (Definition 2.5) also controls the amount of incompressibility. Large values of ν (incompressible) results from large values of λ. For large values of λ compared to μ, the elastic energy is dominated by
. Consequently, a value of one characterizes incompressibility. Let us recall, the Poisson ratio ν in the linear elastic model (Definition 2.5) also controls the amount of incompressibility. Large values of ν (incompressible) results from large values of λ. For large values of λ compared to μ, the elastic energy is dominated by 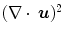 . The Jacobian determinant can by approximated by
. The Jacobian determinant can by approximated by 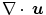 if the
if the 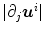 are sufficiently small:
are sufficiently small:
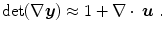
This shows the approximate behavior of linear elastic regularization. To conclude, hyperelastic regularization holds for large deformations whereas linear elastic regularization is restricted to small deformations. Further, the area energy term in hyperelastic regularization, which is missing in elastic regularization, serves as a link between the length and volume term [22].
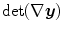 represents the exact volume change due to a transformation
represents the exact volume change due to a transformation 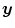 . Consequently, a value of one characterizes incompressibility. Let us recall, the Poisson ratio ν in the linear elastic model (Definition 2.5) also controls the amount of incompressibility. Large values of ν (incompressible) results from large values of λ. For large values of λ compared to μ, the elastic energy is dominated by
. Consequently, a value of one characterizes incompressibility. Let us recall, the Poisson ratio ν in the linear elastic model (Definition 2.5) also controls the amount of incompressibility. Large values of ν (incompressible) results from large values of λ. For large values of λ compared to μ, the elastic energy is dominated by 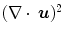 . The Jacobian determinant can by approximated by
. The Jacobian determinant can by approximated by 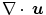 if the
if the 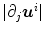 are sufficiently small:
are sufficiently small: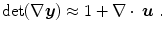
(2.21)
2.1.3 B-Spline Transformation
So far only non-parametric transformations were discussed. However, in some cases the search space for the desired transformation can be restricted by using a suitable parametric transformation model. As an example, for many brain alignment tasks the transformation can be assumed to be rigid. This can increase the robustness of the registration task. The most prominent parametric transformations are scaling, rigid, affine, and spline-based transformations [95]. For non-linear transformations, as required for PET motion estimation, the parametric B-spline transformation is of particular interest.
In parametric image registration the transformation is given in terms of a parametric function 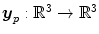 .
. 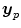 is defined by a parameter vector p. The task is to find the parameter set p minimizing the distance between
is defined by a parameter vector p. The task is to find the parameter set p minimizing the distance between 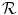 and the transformed input image
and the transformed input image 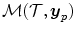
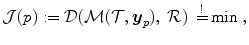
where 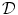 is a data term according to Sect. 2.1.1 and
is a data term according to Sect. 2.1.1 and 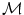 is a transformation model according to Eq. (2.2) or (2.46).
is a transformation model according to Eq. (2.2) or (2.46).
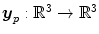 .
. 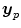 is defined by a parameter vector p. The task is to find the parameter set p minimizing the distance between
is defined by a parameter vector p. The task is to find the parameter set p minimizing the distance between 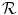 and the transformed input image
and the transformed input image 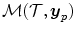
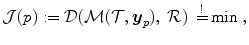
(2.22)
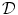 is a data term according to Sect. 2.1.1 and
is a data term according to Sect. 2.1.1 and 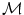 is a transformation model according to Eq. (2.2) or (2.46).
is a transformation model according to Eq. (2.2) or (2.46).Definition 2.8 (Spline transformation).
Given a number 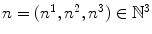 of spline coefficients and a spline basis function
of spline coefficients and a spline basis function 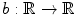 , the spline transformation or free-form transformation
, the spline transformation or free-form transformation 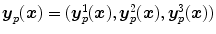 for a point
for a point 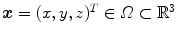 is defined as
is defined as
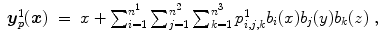
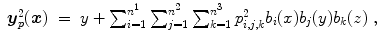
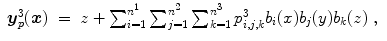
where
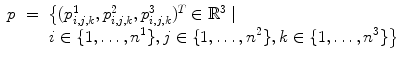
are the spline coefficients and 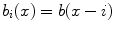 for i ∈ { 1, …, n 1},
for i ∈ { 1, …, n 1}, 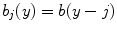 for j ∈ { 1, …, n 2},
for j ∈ { 1, …, n 2}, 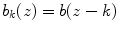 for k ∈ { 1, …, n 3}. Note that this notation is only valid for
for k ∈ { 1, …, n 3}. Note that this notation is only valid for 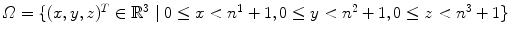 .
.
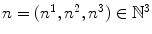 of spline coefficients and a spline basis function
of spline coefficients and a spline basis function 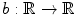 , the spline transformation or free-form transformation
, the spline transformation or free-form transformation 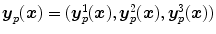 for a point
for a point 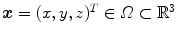 is defined as
is defined as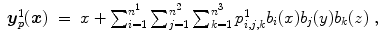
(2.23)
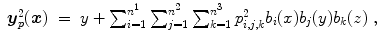
(2.24)
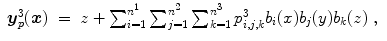
(2.25)
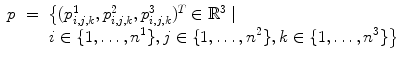
(2.26)
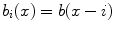 for i ∈ { 1, …, n 1},
for i ∈ { 1, …, n 1}, 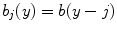 for j ∈ { 1, …, n 2},
for j ∈ { 1, …, n 2}, 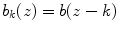 for k ∈ { 1, …, n 3}. Note that this notation is only valid for
for k ∈ { 1, …, n 3}. Note that this notation is only valid for 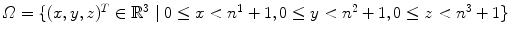 .
.
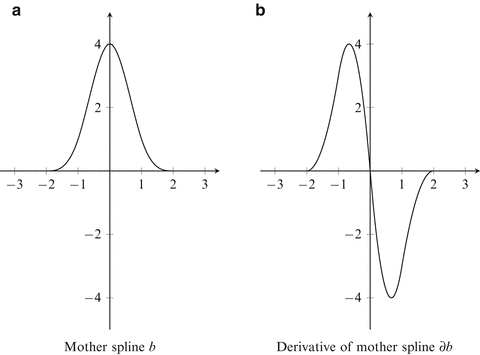
Fig. 2.2
The mother spline b defined in Eq. (2.27) is shown in (a). b is continuously differentiable and its derivative is plotted in (b)
Parametric transformations are implicitly regularized by the reduced number of parameters compared to non-parametric transformations, as discussed in Sect. 2.1.2. Hence, regularization of, e.g., rigid or affine transformations, is usually not necessary. However, regularization becomes of importance for spline transformations due to the non-linearity [48]. Possible regularization variants for spline transformations are discussed in the following. For parametric transformations the functional in Eq. (2.22) becomes
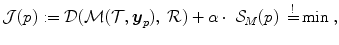
for a regularization term  and a scalar weighting factor
and a scalar weighting factor ![$$\alpha \in \mathbb{R}^{>0}$$
” src=”/wp-content/uploads/2016/09/A319392_1_En_2_Chapter_IEq98.gif”></SPAN> balancing between the data and regularization term.</DIV><br />
<DIV id=Sec12 class=]()
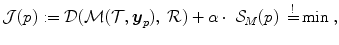
(2.28)
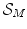 and a scalar weighting factor
and a scalar weighting factor 2.1.3.1 Hyperelastic Regularization
Hyperelastic regularization, introduced for non-parametric transformations in Definition 2.7, can also be applied to the B-spline transformation model. The transformation 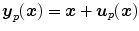 is written in the discrete setting of [95] as
is written in the discrete setting of [95] as
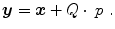
The deformation 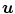 is represented by a projection of the spline coefficients, given by the parameter vector p, into the image space by the projection matrix Q
is represented by a projection of the spline coefficients, given by the parameter vector p, into the image space by the projection matrix Q
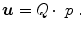
For the hyperelastic regularization the transformation 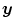 is first determined according to Eq. (2.29) and is then regularized as described in Eq. (2.17). The regularization functional in Eq. (2.28) is then defined as
is first determined according to Eq. (2.29) and is then regularized as described in Eq. (2.17). The regularization functional in Eq. (2.28) is then defined as
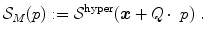
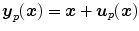 is written in the discrete setting of [95] as
is written in the discrete setting of [95] as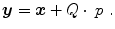
(2.29)
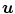 is represented by a projection of the spline coefficients, given by the parameter vector p, into the image space by the projection matrix Q
is represented by a projection of the spline coefficients, given by the parameter vector p, into the image space by the projection matrix Q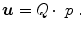
(2.30)
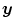 is first determined according to Eq. (2.29) and is then regularized as described in Eq. (2.17). The regularization functional in Eq. (2.28) is then defined as
is first determined according to Eq. (2.29) and is then regularized as described in Eq. (2.17). The regularization functional in Eq. (2.28) is then defined as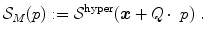
(2.31)
2.1.3.2 Coefficient-Based Regularization
The regularization term 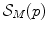 in Eq. (2.28) is based on the coefficient vector p in the case of coefficient-based regularization and is a weighted norm of the form
in Eq. (2.28) is based on the coefficient vector p in the case of coefficient-based regularization and is a weighted norm of the form
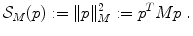
The matrix M determines the regularization type. Instead of regularizing the deformation 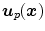 for each spatial position
for each spatial position 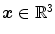 as in the non-parametric case (cf. Sect. 2.1.2) we now regularize directly on p. We speak of coefficient-based regularization in image space if the regularization on p considers the projection matrix Q and thus regularizes Q ⋅ p. If only p is taken into account we speak of coefficient-based regularization in coefficient space.
as in the non-parametric case (cf. Sect. 2.1.2) we now regularize directly on p. We speak of coefficient-based regularization in image space if the regularization on p considers the projection matrix Q and thus regularizes Q ⋅ p. If only p is taken into account we speak of coefficient-based regularization in coefficient space.
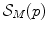 in Eq. (2.28) is based on the coefficient vector p in the case of coefficient-based regularization and is a weighted norm of the form
in Eq. (2.28) is based on the coefficient vector p in the case of coefficient-based regularization and is a weighted norm of the form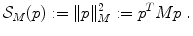
(2.32)
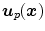 for each spatial position
for each spatial position 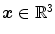 as in the non-parametric case (cf. Sect. 2.1.2) we now regularize directly on p. We speak of coefficient-based regularization in image space if the regularization on p considers the projection matrix Q and thus regularizes Q ⋅ p. If only p is taken into account we speak of coefficient-based regularization in coefficient space.
as in the non-parametric case (cf. Sect. 2.1.2) we now regularize directly on p. We speak of coefficient-based regularization in image space if the regularization on p considers the projection matrix Q and thus regularizes Q ⋅ p. If only p is taken into account we speak of coefficient-based regularization in coefficient space.With Tikhonov regularization we will discuss one option for coefficient-based regularization in coefficient space. Tikhonov regularization punishes gradients in the spline coefficients and is the coefficient-based analog of diffusion regularization introduced in Definition 2.3.
Definition 2.9 (Tikhonov regularization (coefficient space)).
Tikhonov regularization in coefficient space is defined by the choice of
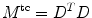
in Eq. (2.32). The superscript tc denotes (t)ikhonov in (c)oefficient space. D is defined by
![$$\displaystyle{ D = I_{3}\otimes \left [\begin{array}{*{10}c} D^{1} \\ D^{2} \\ D^{3} \end{array} \right ]\;. }$$](/wp-content/uploads/2016/09/A319392_1_En_2_Chapter_Equ34.gif)
Here I 3 is the 3 × 3 identity matrix and ⊗ denotes the Kronecker product [16]. The 1D derivative operators are defined by
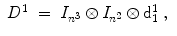
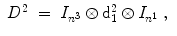
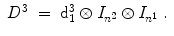
The 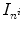 denote identity matrices with the size n i × n i , i ∈ { 1, 2, 3}, and the n i defined according to Definition 2.8. The discrete 1D first derivative operators for each dimension are defined by
denote identity matrices with the size n i × n i , i ∈ { 1, 2, 3}, and the n i defined according to Definition 2.8. The discrete 1D first derivative operators for each dimension are defined by
![$$\displaystyle{ \mathrm{d}_{1}^{i} = \left [\begin{array}{*{10}c} -1&1& &0\\ & \ddots & \ddots & \\ 0 & &-1&1 \end{array} \right ] \in \mathbb{R}^{n^{i}-1,n^{i} },\;i \in \{ 1,2,3\}\;. }$$](/wp-content/uploads/2016/09/A319392_1_En_2_Chapter_Equ38.gif)
(2.33)
![$$\displaystyle{ D = I_{3}\otimes \left [\begin{array}{*{10}c} D^{1} \\ D^{2} \\ D^{3} \end{array} \right ]\;. }$$](/wp-content/uploads/2016/09/A319392_1_En_2_Chapter_Equ34.gif)
(2.34)
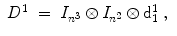
(2.35)
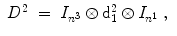
(2.36)
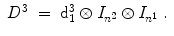
(2.37)
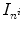 denote identity matrices with the size n i × n i , i ∈ { 1, 2, 3}, and the n i defined according to Definition 2.8. The discrete 1D first derivative operators for each dimension are defined by
denote identity matrices with the size n i × n i , i ∈ { 1, 2, 3}, and the n i defined according to Definition 2.8. The discrete 1D first derivative operators for each dimension are defined by![$$\displaystyle{ \mathrm{d}_{1}^{i} = \left [\begin{array}{*{10}c} -1&1& &0\\ & \ddots & \ddots & \\ 0 & &-1&1 \end{array} \right ] \in \mathbb{R}^{n^{i}-1,n^{i} },\;i \in \{ 1,2,3\}\;. }$$](/wp-content/uploads/2016/09/A319392_1_En_2_Chapter_Equ38.gif)
(2.38)
The analog of the above definition in image space is given with the following Definition 2.10. As the real displacements and not the corresponding coefficients are processed, this version is even more related to the diffusion regularization energy in Definition 2.3.
Definition 2.10 (Tikhonov regularization (image space)).
Let the number of spline coefficients be 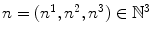 and
and 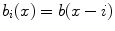 for i ∈ { 1, …, n d }, d ∈ { 1, 2, 3}, be the translated spline basis function b defined in Eq. (2.27). The Tikhonov regularization matrix in image space is defined as
for i ∈ { 1, …, n d }, d ∈ { 1, 2, 3}, be the translated spline basis function b defined in Eq. (2.27). The Tikhonov regularization matrix in image space is defined as
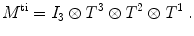
The matrices 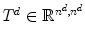 are defined by
are defined by
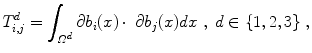
where i ∈ { 1, …, n d }, j ∈ { 1, …, n d }, and 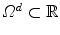 is the 1D subspace of Ω in dimension d ∈ { 1, 2, 3}.
is the 1D subspace of Ω in dimension d ∈ { 1, 2, 3}.
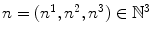 and
and 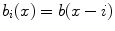 for i ∈ { 1, …, n d }, d ∈ { 1, 2, 3}, be the translated spline basis function b defined in Eq. (2.27). The Tikhonov regularization matrix in image space is defined as
for i ∈ { 1, …, n d }, d ∈ { 1, 2, 3}, be the translated spline basis function b defined in Eq. (2.27). The Tikhonov regularization matrix in image space is defined as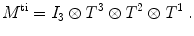
(2.39)
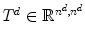 are defined by
are defined by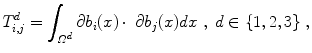
(2.40)
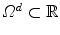 is the 1D subspace of Ω in dimension d ∈ { 1, 2, 3}.
is the 1D subspace of Ω in dimension d ∈ { 1, 2, 3}.The concrete numbers for the matrix T d (including boundary treatment) are
![$$\displaystyle{ T^{d}=\left [\begin{array}{*{10}c} 15.1 &-5.0&-7.2&-0.3& & & & & 0\\ -5.0 & 23.9 &-4.5 &-7.2 &-0.3 & & & & \\ -7.2&-4.5& 24.0 &-4.5&-7.2&-0.3& & &\\ -0.3 &-7.2 &-4.5 & 24.0 &-4.5 &-7.2 &-0.3 && \\ & \ddots & \ddots & \ddots & \ddots & \ddots & \ddots & \ddots &\\ & &-0.3 &-7.2 &-4.5 & 24.0 &-4.5 &-7.2&-0.3 \\ & & &-0.3&-7.2&-4.5& 24.0 &-4.5&-7.2\\ & & & &-0.3 &-7.2 &-4.5 & 23.9 &-5.0 \\ 0 & & & & &-0.3&-7.2&-5.0& 15.1 \end{array} \right ] \in \mathbb{R}^{n^{d},n^{d} } }$$](/wp-content/uploads/2016/09/A319392_1_En_2_Chapter_Equ41.gif)
(2.41)
for d ∈ { 1, 2, 3}. The entries of the matrix T d are obtained by calculating the integral in Eq. (2.40) for each index i ∈ { 1, …, n d } and j ∈ { 1, …, n d }, d ∈ { 1, 2, 3}.
2.1.4 Mass-Preserving Image Registration
The standard transformation model for image registration in Eq. (2.2) does not guarantee the preservation of mass, i.e., in general
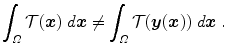
Further, the distance functional 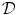 typically entails the assumption of similar intensities at corresponding points. This assumption is not valid for the standard transformation model
typically entails the assumption of similar intensities at corresponding points. This assumption is not valid for the standard transformation model 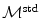 in case of dual gated PET as discussed in connection with Fig. 1.11. Consequently, the standard transformation model needs some modification to express this feature.
in case of dual gated PET as discussed in connection with Fig. 1.11. Consequently, the standard transformation model needs some modification to express this feature.
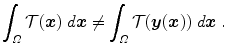
(2.42)
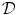 typically entails the assumption of similar intensities at corresponding points. This assumption is not valid for the standard transformation model
typically entails the assumption of similar intensities at corresponding points. This assumption is not valid for the standard transformation model 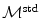 in case of dual gated PET as discussed in connection with Fig. 1.11. Consequently, the standard transformation model needs some modification to express this feature.
in case of dual gated PET as discussed in connection with Fig. 1.11. Consequently, the standard transformation model needs some modification to express this feature.The requirement for the desired transformation model 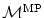 is the preservation of mass
is the preservation of mass
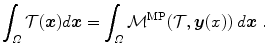
From the integration by substitution theorem for multiple variables we know that the following equation holds
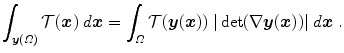
With respect to PET, Eq. (2.44) guarantees already the same total amount of radioactivity before and after applying the transformation 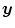 to
to 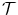 . The Jacobian determinant
. The Jacobian determinant 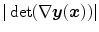 accounts for the volume change induced by the transformation
accounts for the volume change induced by the transformation 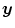 , representing the mass-preserving component. As
, representing the mass-preserving component. As 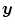 should reflect cardiac and respiratory motion, transformations that are not bijective are anatomically not meaningful and have therefore to be excluded. For example, the hyperelastic regularization functional in Sect. 2.1.2.3 guarantees
should reflect cardiac and respiratory motion, transformations that are not bijective are anatomically not meaningful and have therefore to be excluded. For example, the hyperelastic regularization functional in Sect. 2.1.2.3 guarantees 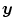 to be diffeomorphic and orientation preserving, which allows us to drop the absolute value bars
to be diffeomorphic and orientation preserving, which allows us to drop the absolute value bars
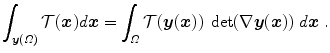
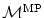 is the preservation of mass
is the preservation of mass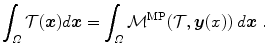
(2.43)
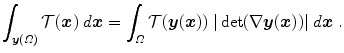
(2.44)
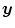 to
to 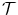 . The Jacobian determinant
. The Jacobian determinant 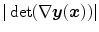 accounts for the volume change induced by the transformation
accounts for the volume change induced by the transformation 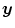 , representing the mass-preserving component. As
, representing the mass-preserving component. As 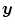 should reflect cardiac and respiratory motion, transformations that are not bijective are anatomically not meaningful and have therefore to be excluded. For example, the hyperelastic regularization functional in Sect. 2.1.2.3 guarantees
should reflect cardiac and respiratory motion, transformations that are not bijective are anatomically not meaningful and have therefore to be excluded. For example, the hyperelastic regularization functional in Sect. 2.1.2.3 guarantees 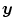 to be diffeomorphic and orientation preserving, which allows us to drop the absolute value bars
to be diffeomorphic and orientation preserving, which allows us to drop the absolute value bars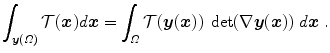
(2.45)
We derived the Vampire (Variational Algorithm for Mass-Preserving Image REgistration) based on the above considerations in our previous work [51]. The source code of Vampire can be downloaded at [52].
Definition 2.11 (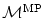 – Mass-preserving transformation model).
– Mass-preserving transformation model).
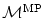 – Mass-preserving transformation model).
– Mass-preserving transformation model).For an image 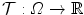 on the domain
on the domain 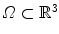 and a transformation
and a transformation 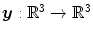 the mass-preserving transformation model is defined as
the mass-preserving transformation model is defined as
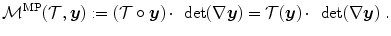
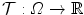 on the domain
on the domain 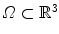 and a transformation
and a transformation 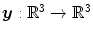 the mass-preserving transformation model is defined as
the mass-preserving transformation model is defined as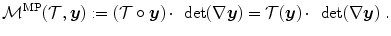
(2.46)
In the mass-preserving transformation model of Vampire the template image 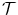 is transformed by interpolation on the deformed grid
is transformed by interpolation on the deformed grid 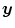 with an additional multiplication by the volume change. The multiplication by the Jacobian is a physiological and realistic modeling for density-based images [128, 138]. It guarantees similar intensities at corresponding points after transformation with a simultaneous preservation of the total amount of radioactivity.
with an additional multiplication by the volume change. The multiplication by the Jacobian is a physiological and realistic modeling for density-based images [128, 138]. It guarantees similar intensities at corresponding points after transformation with a simultaneous preservation of the total amount of radioactivity.
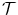 is transformed by interpolation on the deformed grid
is transformed by interpolation on the deformed grid 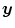 with an additional multiplication by the volume change. The multiplication by the Jacobian is a physiological and realistic modeling for density-based images [128, 138]. It guarantees similar intensities at corresponding points after transformation with a simultaneous preservation of the total amount of radioactivity.
with an additional multiplication by the volume change. The multiplication by the Jacobian is a physiological and realistic modeling for density-based images [128, 138]. It guarantees similar intensities at corresponding points after transformation with a simultaneous preservation of the total amount of radioactivity.A simple 2D example for the mass-preserving transformation model is shown in Fig. 2.3 for illustration. We will use the same notation as in the 3D case for 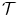 ,
, 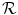 , Ω,
, Ω, 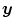 , and
, and 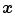 . Thus, we redefine
. Thus, we redefine 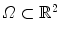 ,
, 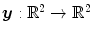 , and
, and 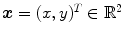 for the 2D example.
for the 2D example. 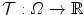 and
and 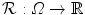 are defined in the same way but for the new domain Ω.
are defined in the same way but for the new domain Ω.
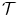 ,
, 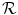 , Ω,
, Ω, 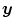 , and
, and 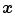 . Thus, we redefine
. Thus, we redefine 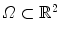 ,
, 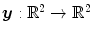 , and
, and 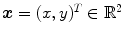 for the 2D example.
for the 2D example. 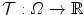 and
and 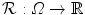 are defined in the same way but for the new domain Ω.
are defined in the same way but for the new domain Ω.
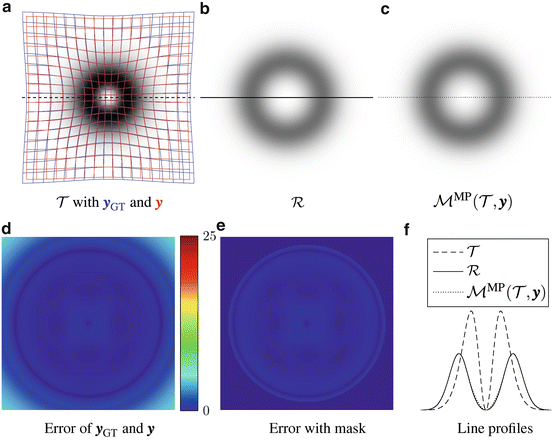
Fig. 2.3
2D example for the mass-preserving transformation model. The template image 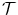 in (a) is registered to the reference image
in (a) is registered to the reference image 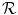 in (b) with Vampire resulting in (c). The average endpoint error e between the estimated transformation
in (b) with Vampire resulting in (c). The average endpoint error e between the estimated transformation 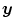 and the ground-truth transformation
and the ground-truth transformation 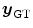 is visualized in (d). The same plot restricted to a mask where
is visualized in (d). The same plot restricted to a mask where  and
and  have an intensity above 1 is shown in (e). The color map for both error plots is given in-between. Line profiles are shown in (f)
have an intensity above 1 is shown in (e). The color map for both error plots is given in-between. Line profiles are shown in (f)
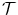 in (a) is registered to the reference image
in (a) is registered to the reference image 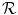 in (b) with Vampire resulting in (c). The average endpoint error e between the estimated transformation
in (b) with Vampire resulting in (c). The average endpoint error e between the estimated transformation 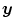 and the ground-truth transformation
and the ground-truth transformation 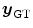 is visualized in (d). The same plot restricted to a mask where
is visualized in (d). The same plot restricted to a mask where 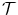 and
and 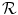 have an intensity above 1 is shown in (e). The color map for both error plots is given in-between. Line profiles are shown in (f)
have an intensity above 1 is shown in (e). The color map for both error plots is given in-between. Line profiles are shown in (f)The images of the example are constructed to be similar to SA views of the heart to a certain degree, cf. Fig. 1.14b. Further, they have the same total mass (by construction) and thus exactly fulfill the conditions for mass-preservation. The template and reference image represent smooth signals based on Gaussian distributions. The template image is created by subtracting two Gaussian distributions with different standard deviation 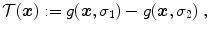
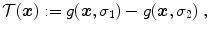
(2.47)
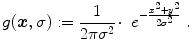
(2.48)
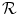 is created by applying a known transformation
is created by applying a known transformation 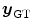 to
to  according to the mass-preserving transformation model
according to the mass-preserving transformation model 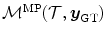 in Eq. (2.46). Hence,
in Eq. (2.46). Hence, 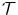 and
and 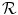 have the same global mass. The ground-truth transformation is defined by
have the same global mass. The ground-truth transformation is defined by