Fig. 5.1
(a) ASM model highlighting main components of the encoding of a force response by [Ca2+]cyt where propagating [Ca2+]cyt oscillations give rise to a sustained force response. (b) Demonstration of the sustained response of force due to a sequence of [Ca2+]cyt increases by flash photolytic release of caged Ca2+. (c) Decreasing the flash interval time of photolytic release of Ca2+ resulted in a correlated increase in level of steady-state force
The [Ca2+]cyt response to agonist stimulation, which oscillates, travels as a wave which radiates out from a discrete site. The “Ca2 + wave” usually originates from the same site within an ASM cell after repeated stimulus and also maintains the same wave front direction across the cytosol [73, 79, 81]. Also, before stimulation, spontaneous yet spatially isolated [Ca2 +]cyt transients, known as “Ca2 + sparks,” can be observed at random locations within the ASM cell [73]. Ca2 + sparks are rapid with an estimated rise time of ~30–90 ms and fall time of ~60–300 ms [73]. Ca2 + sparks are attributed to the activation kinetics of RyR channels [72, 73, 96]. The Ca2 + spark, a stochastic event, is the most elementary of Ca2 + release events [72, 73, 96].
The frequency as well as propagation velocity of [Ca2 +]cyt oscillations increases with agonist concentration [79, 81] and may be reflections of RyR-mediated CICR sensitivity [81]. Frequency modulation of [Ca2 +]cyt during agonist stimulation is proposed as a mode of control of the contractile response (Fig. 5.1) [79, 81].
Excitation-Contraction Coupling Time Frame
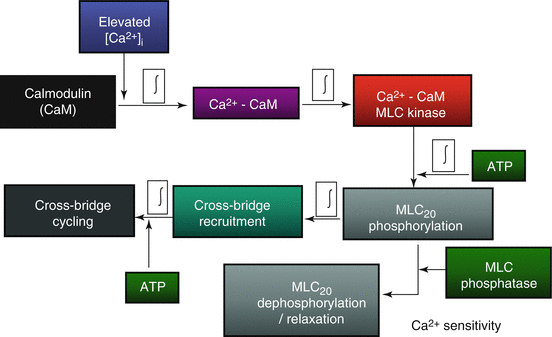
When ASM cells are exposed to 1 μM ACh, an elevation in [Ca2 +]cyt is induced, yet evidence of muscle shortening is delayed by several hundred milliseconds [94]. This time delay reflects the time required for a cascade of events (Fig. 5.2) that can be summarized into four main steps: (1) mobilization of CaM, (2) binding of Ca2+ to CaM and subsequent activation of MLCK, (3) phosphorylation of MLC20, and finally (4) crossbridge recruitment. The relative contribution of each the four delays have been quantified in ASM by measuring the response to rapid (virtually instantaneous) release of caged compounds by flash photolysis [94]. The results of this study indicate that mobilization of CaM is the most significant delay, while the delay due to phosphorylation of MLC20 and crossbridge recruitment is minor [94].
Mechanical Function and ATP Hydrolysis
The primary role of muscle (skeletal muscle or smooth muscle) is to perform mechanical work through contraction force generation. To perform mechanical work, muscles require chemical energy in the form of ATP hydrolysis. The relationship between muscle work and ATP hydrolysis is not as well defined in smooth muscle compared to skeletal muscle. Therefore, to provide a conceptual framework for the dynamic range of energy demand in smooth muscle, the relationship between mechanical work and energy consumption in skeletal muscle will serve as a point of reference.
The molecular mechanism responsible for contraction in smooth muscle, like all muscle, is the contractile protein apparatus, actin and myosin, conferred by its dual ability to enzymatically harvest chemical energy and, subsequently, perform mechanical work. Chemical energy is harvested via ATP hydrolysis by the actin-activated myosin ATPase (actomyosin ATPase). The energy released by hydrolysis of ATP is coupled to the intrinsic force development by cyclic attachment and detachment of myosin heads to actin (crossbridge cycling).
The intrinsic structural unit that underlies force generation and contraction in skeletal muscle is the actin-myosin crossbridge. Andrew Huxley originally proposed this relationship in a simple model where crossbridge cycling reflected the repetitive transition between two possible mechanical states: (1) myosin attached to actin and generating force and (2) myosin detached from actin [53, 54]. In this model, the hydrolysis of ATP occurs during the transition between attached and detached states. Thus, the Huxley model provides a simplified conceptual framework for both excitation-contraction coupling and excitation-energy coupling.
Skeletal muscle actin-myosin orientation is precisely ordered into units of repeating architecture referred to as sarcomeres – which are important context for application of the Huxley model to skeletal muscle. In brief, the sarcomere is made up of an interlacing, crystalline formation of thick filaments (myosin) and thin filaments (actin). The boundary of a sarcomere is formed by a dense Z-disk or Z-line, which fasten the actin filaments. Actin filaments extend from Z-line to the midline of the sarcomere. The myosin filaments, centered at the midline of the sarcomere, lie between and parallel to actin filaments such that there are six actin filaments surrounding each myosin filament. During muscle contraction, crossbridge cycling within the overlapping regions of the actin and myosin filaments within a half-sarcomere pulls its associated Z-line towards the midline. Thus, the force and contraction vectors are determined by actin-myosin crossbridges within a half-sarcomere. For more details, see review by [93].
The Huxley model has been expanded to a quantitative form by [8, 9]. To summarize, the fraction of strongly bound crossbridges in the force-generating state (Huxley’s two-state model) is represented as “α fs”. A strongly bound crossbridge is able to supply a unit of force, which is approximated as an averaged quantity of force per crossbridge and designated by “f”. The maximal number of myosin heads available for crossbridges formation within a half-sarcomere is represented as “n”. The combination of these factors determines force (F) generated by a muscle fiber as shown in Eq. 5.1.
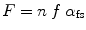
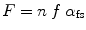
(5.1)
The fraction of crossbridges in a force-generating state (α fs) is a function of the rates of transition between the two mechanical/structural states of the Huxley model as shown in Eq. 5.2 below, where “ƒapp” is the apparent rate constant for transition to the attached state, and “g app” is the apparent rate constant for transition to the detached state.
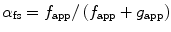
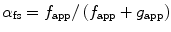
(5.2)
Relationships that characterize skeletal muscle function (force vs. Ca2+, force vs. length, and force vs. cross-sectional area) can be accounted for by this model. The parameter α fs can be increased by an increase in [Ca2 +]cyt which promotes transition to the attached, force-generating state of crossbridges (force-Ca2+ relationship). Muscle length, which in turn defines sarcomere length and the extent of actin-myosin filament overlap, also affects α fs without an effect on n (force-length relationship). Finally, fiber cross-sectional area reflects the number of sarcomeres in parallel and, thus, myosin content per half-sarcomere (myosin content determines n) [95].
Using this conceptual framework, a relationship can also be described for ATP consumption assuming a stoichiometry of 1 mole ATP consumed per crossbridge detachment. This relationship is shown in Eq. 5.3 where “b” represents the number of half-sarcomeres within the fiber.
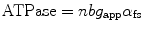
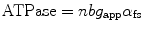
(5.3)
The load opposing the intrinsic crossbridge-induced sarcomeric contraction slows crossbridge cycling rate due to its effect on g app. From Eq. 5.2, this slowing of g app has the effect of increasing α fs and thereby increasing force generation to the point where there is no contraction (isometric force). The rate of contraction (shortening velocity) depends inversely on external load imposed on the sarcomere and therefore determines the force (or load)-velocity relationship. From Eq. 5.3, the rate of ATP hydrolysis (“ATPase” in Eq. 5.3) also depends on g app; thus, external load and intrinsic force generation opposing the load will influence the rate of ATP hydrolysis. The direct relationship between heat (reflecting energy consumption) and power output of muscle due to contraction (the product of force and shortening velocity) is known as the Fenn effect and was first described in 1923 [29]. Thus, the maximum rate of ATP hydrolysis occurs at peak power output in skeletal muscle [93, 95, 97].
In skeletal muscle fibers, isometric force generation at any given level of Ca2 + activation is accompanied by a sustained rate of ATP hydrolysis as described by Eq. 5.3 [95] .Thus, the energy cost of force generation does not change during a given level of isometric activation. In contrast, during sustained isometric force generation of smooth muscle, the rate of ATP hydrolysis decreases with time even as force is sustained [25, 48, 104]. This indicates that in smooth muscle, the energy cost of producing force decreases with time – sustained smooth muscle force generation becomes more energy efficient. The energy cost of force generation in smooth muscle can be explained by the Huxley model with consideration of the differences between smooth and skeletal muscle mechanics. For example, there are key differences in actin-myosin alignment, actin-myosin remodeling, and Ca2 + regulation of crossbridge recruitment. Each of these factors will be considered in the next sections.
Actin-Myosin Alignment
Monomeric myosin is assembled into polymers or thick filaments in a nonhelical, side-polar configuration in smooth muscle [50, 110], while in skeletal muscle myosin filaments form a helical, bipolar configuration (Fig. 5.3). The bipolar arrangement forms a “bare area” at the middle of the myosin thick filament. This bare area and the steric constraints of the sarcomeric structure impose limits on muscle length in skeletal muscle that do not exist in smooth muscle. The side-polar arrangement of actin-myosin filaments in smooth muscle allows a significantly greater length range [91, 110].
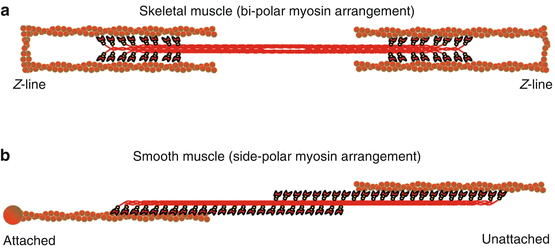

Fig. 5.3
(a) Schematic representation of the bipolar arrangement of myosin in skeletal muscle and (b) the side-polar arrangement of myosin in smooth muscle. The interaction of myosin (red) with actin (brown) is compared between both muscle types where in skeletal muscle (a) actin-myosin structure is fastened by Z-lines whereas in smooth muscle (b) the actin-myosin lattice structure is dynamic and can potentially be fastened to dense bodies or membrane-associated dense plaques (represented by the attached end) and/or potentially unloaded (Represented by the unattached end)
Actin-Myosin Remodeling
In both smooth and skeletal muscle, myosin thick filaments interact with actin thin filaments to form crossbridges. However, in skeletal muscle, actin filaments are anchored in a regular fashion by the Z-disks of the sarcomere, whereas in smooth muscle, actin filaments are clustered into regions called dense bodies or membrane-associated dense plaques (Fig. 5.3) [39, 93]. The dense bodies fasten the side-polar actin-myosin lattice and allow force transmission [50, 63] – analogous to the Z-disk in skeletal muscle sarcomeres [39]. However, the internal arrangement of the contractile apparatus (actin-myosin filaments, dense bodies, and dense plaques) in smooth muscle is not regularly ordered and may undergo remodeling during the contractile response (see reviews [41, 91, 113]). Thus, although external isometric conditions may be maintained, dynamic internal remodeling may change the length and overlap relationships between actin and myosin filaments. From Eq. 5.1, force in skeletal muscle is dependent on the number of myosin heads (n) and the fraction of myosin heads forming crossbridges (α fs). Actin and myosin filament remodeling in smooth muscle will affect both n and α fs. In addition, actin and myosin filament remodeling will result in changes in internal loading that affect crossbridge cycling rate (g app from Eq. 5.2), α fs (Eq. 5.1), and the rate of ATP hydrolysis (Eq. 5.3).
There is evidence of changes in actin polymerization during Ca2 + activation and force generation in smooth muscle [40, 49, 68]. Actin exists in two distinct but interchangeable forms: polymeric, filamentous actin (F-actin) and monomeric actin (G-actin) [41, 58, 68]. During contraction, there is a decrease in G-actin content in ASM [68]. Pharmacological inhibition of actin polymerization reduces isometric force generation in smooth muscle [40, 58, 68], which suggests that actin polymerization plays an important role in the contractile response. In addition to actin polymerization, there is a reorganization of the contractile network through myosin polymerization [1, 55, 64, 65, 91] that changes the length of the myosin filaments and thus the number of myosin heads that can potentially form crossbridges (n in Eq. 5.1). Filamentous actin is also coupled to the extracellular matrix (ECM) by focal adhesion complexes (membrane-bound dense plaques) [40]. Focal adhesion complexes are comprised of a scaffold of structural and signaling proteins, including mechanosensitive transmembrane integrins [41, 113]. The location of focal adhesion complexes around the PM is dynamically regulated during contraction [3, 32]. In other cell types which are motile, focal adhesions orchestrate actin polymerization to cause cell movement [41, 113]. A similar process may occur in the ASM where focal adhesions recruit actin polymerization (increasing internal loading) according to local mechanical stimuli.
In addition to internal aspects of a contractile stimulus, the ECM transmits mechanical loads (external load) onto the focal adhesions. This external load in vivo is dynamic due to inflation and deflation of the lung [40, 41, 113]. Dynamic changes in external loading may stimulate changes (perhaps via integrin-mediated pathways) in actin-myosin filament architecture. The actin-myosin architecture at any given moment is therefore a function of the history of mechanical stimuli [39, 49, 64] and influences internal loading of crossbridges.
Mechanisms of Ca2+-Induced Activation
In response to an elevation of [Ca2 +]cyt,, crossbridge recruitment in smooth muscle is myosin-activated, whereas in skeletal muscle Ca2 + regulation of crossbridge recruitment is actin-regulated. Skeletal muscle actin is associated with other proteins, troponin and tropomyosin, that regulate exposure of the myosin-binding site on actin. In skeletal muscle, with an increase in [Ca2 +]cyt, troponin C binds Ca2 +, which induces a conformational change in troponin I and troponin T followed by transposition of tropomyosin uncovering the myosin-binding site on the actin filament. With the myosin-binding site uncovered, crossbridge recruitment and cycling proceeds [93].
In contrast, in smooth muscle, Ca2 +-dependent regulation of crossbridge recruitment requires phosphorylation of the regulatory domain of myosin (MLC20) by myosin light-chain kinase (MLCK) (Fig. 5.2). MLCK activity is stimulated by an increase in [Ca2 +]cyt through the binding of Ca2 + to calmodulin (CaM). The extent of MLC20 phosphorylation is also regulated by myosin light-chain phosphatase (MLCP), which is not Ca2+-dependent but is regulated by a Rho kinase pathway [98]. As a consequence, the phosphorylation of MLC20 reflects the balance between MLCK and MLCP activities and, therefore, Ca2 +-dependent and independent (i.e., Ca2 + sensitivity) mechanisms.
“Latch-Bridge” Hypothesis
Smooth muscle force generation and contraction is generally initiated by a transient elevation of [Ca2 +]cyt with an associated transient increase in MLC20 phosphorylation. Yet, force generation in smooth muscle can be maintained at a constant level despite transients in [Ca2 +]cyt or MLC20 phosphorylation. Therefore, there are two distinct phases of force generation in smooth muscle initiated by a transient elevation of [Ca2 +]cyt: (1) the initial increase in both force and MLC20 phosphorylation and (2) the maintenance of force despite decreasing [Ca2 +]cyt and MLC20 phosphorylation. This second phase of smooth muscle activation is also associated with a slowing of shortening velocity (crossbridge cycling rate) and has been termed the “latch state” [44, 69]. According to this hypothesis, a unique crossbridge state – the “latch-bridge” – is formed when the myosin head of an attached crossbridge (due to prior MLC20 phosphorylation) is then dephosphorylated. These “latch-bridges” cycle at a slower rate with an increased duty cycle (amount of time attached vs. detached) and, therefore, maintain force at a lower level of MLC20 phosphorylation or [Ca2 +]cyt reflecting increased Ca2 + sensitivity of force generation. The main assumption of the latch-bridge model is that the extent of MLC20 phosphorylation determines the “latch” or energetic state of smooth muscle force generation [44].
In a Triton X-100 permeabilized ASM preparation [57] directly tested the latch-bridge model by measuring changes in isometric force, MLC20 phosphorylation, and the rate of ATP hydrolysis during maximum Ca2+ activation (10 μM Ca2+). With maximum Ca2+ activation, force increased with a concomitant increase in both MLC20 phosphorylation and the rate of ATP hydrolysis. As Ca2+ activation remained constant, isometric force was sustained, as was the level of MLC20 phosphorylation. However, after peaking, the rate of ATP hydrolysis decreased while force and the level of MLC20 phosphorylation were sustained, reflecting a reduction in energy cost, consistent with a “latch” state, but without a change in MLC20 phosphorylation [57]. To further test the latch-bridge hypothesis, thiophosphorylation (accomplished by incubation with ATPγS) was used to prevent dephosphorylation of MLC20 [57]. After thiophosphorylation, the dynamic change in the rate of ATP hydrolysis with sustained Ca2 + activation was unaffected, also indicating that there is a slowing of crossbridge cycling rate that is independent of any change in the level of MLC20 phosphorylation. This indicates that the level of MLC20 phosphorylation can be dissociated from the rate of ATP hydrolysis and that the “latch-bridge” as proposed does not actually exist.
“Internal Loading” Hypothesis
An alternate “internal loading” hypothesis may explain the decline in the rate of ATP hydrolysis (or energy cost) in ASM during sustained Ca2 + activation [58]. In this hypothesis, internal loading on crossbridges in ASM is not fixed under isometric conditions, but can change by dynamic cytoskeletal remodeling. It has been demonstrated in ASM that inhibition of actin reorganization with phalloidin (which binds F-actin, preventing its depolymerization) significantly lessens the decline in the rate of ATP hydrolysis during sustained Ca2 + activation, thereby increasing the energy cost of force generation [58]. The “internal loading” model can be broken down into two phases: (1) an initial phase when crossbridges are recruited by MLC20 phosphorylation (increasing α fs with an associated increase in the rate of ATP hydrolysis as predicted by Eqs. 5.3 and 5.2) and (2) a delayed phase where there is an increase in internal loading due to cytoskeletal remodeling, with an associated slowing g app and decrease in the rate of ATP hydrolysis (Eq. 5.3). During the initial phase of Ca2+ activation, a portion of the actin-myosin filaments are not fully attached to the internal cytoskeletal structure, resulting in lower internal loading, faster g app, and a high rate of ATP hydrolysis. Subsequently, with cytoskeletal remodeling, there is an increase in actin-myosin filament attachment to the cytoskeleton imposing increased internal loading with a concomitant slowing of the rate of ATP hydrolysis.
Efficiency Versus Power
Peak energy consumption of ASM attains a rate of ~0.12 nmol ATP mm−3 s−1 at peak power output. This is an approximate threefold increase from the ATP consumption rate during maximum isometric force (~0.04 nmol ATP mm−3 s−1) [95]. In contrast, the rate of ATP hydrolysis in skeletal muscle increases from ~1.2 nmol ATP mm−3 s−1 during maximum isometric force generation to ~2.7 nmol ATP mm−3 s−1 during peak power output [95]. The energy cost of force generation in skeletal muscle ranges from ~16,000–35,000 nmol ATP s−1 mN−1 depending on fiber type. In contrast, the energy cost of force generation in smooth muscle is 6–14-fold lower at ~2,500 nmol ATP s−1 mN−1 [95]. The energy demands of skeletal and smooth muscle are reflections of the quality of their mechanical functions. Smooth muscles perform slower, yet sustained mechanical functions, while skeletal muscles are able to achieve more intense mechanical behaviors – the maximum power output of skeletal muscle is ~10–100 times that produced by smooth muscle [95]. Also, in skeletal muscle, there is a relatively large pool of phosphocreatine (PCr) that is available to buffer ATP hydrolysis transients [77]. In contrast, smooth muscle contains a relatively small PCr pool, which indicates a strong dependence on ATP production rather than on PCr buffering [56, 62, 100]. In summary, it appears that the skeletal muscle contractile response is optimized for maximum power output, while it could be argued that smooth muscle is optimized for maximum energy efficiency. Therefore, efficient matching of energy supply with energy demand may be a more significant governing factor for the ASM contractile response.
A Conceptual Framework for the Role of [Ca2+]mito in Excitation-Energy Coupling in ASM
The mitochondria provide for most of the energy demands of the cell by replenishing ATP levels through oxidative phosphorylation. The overall outcome of oxidative phosphorylation is to consume both intramitochondrial NADH and O2 to synthesize ATP from ADP and Pi. In vascular smooth muscle, it is observed that isometric force is strongly correlated to O2 consumption [56, 62, 77], which implies a dependence on mitochondrial oxidative phosphorylation to supply ATP during contraction. Accordingly, this conceptual framework will define energy homeostasis of the ASM during contraction as a two-part system: ATP hydrolysis by actomyosin ATPase and ATP synthesis by oxidative phosphorylation.
Mitochondrial Ca2+ and ATP Production
Due to a substantial amount of evidence to support the role of Ca2 + in cellular energetics, this conceptual framework highlights intramitochondrial Ca2 +([Ca2 +]mito) as principal effector of mitochondrial ATP production, although other effectors (such as ADP [16, 17], Pi [7], O2, and fuel/substrate) likely play a role [11].
An emerging consensus is that elevated [Ca2 +]mito stimulates mitochondrial NADH production which in turn may stimulate ATP production (Fig. 5.4a) [25, 26, 36, 37, 104]. Increased NADH production in response to [Ca2 +]mito can be attributed to Ca2 +-sensitive intramitochondrial dehydrogenases associated with the tricarboxylic acid (TCA) cycle – pyruvate dehydrogenase (PDH), NAD-isocitrate dehydrogenase (ICDH), and oxoglutarate dehydrogenase (OGDH) – which are stimulated by different physiological levels of Ca2 + [25]. The mechanisms by which Ca2 + activates the dehydrogenases are not the same. Specifically, PDH is regulated by PDH-associated kinase and phosphatase – the phosphatase is Ca2 +-sensitive which promotes the active form of PDH. In the case of ICDH and OGDH, Ca2+ binds to the enzyme which increases the enzyme’s affinity for substrate [25]. The relationship between dehydrogenase activity and Ca2 + can also be inhibited by an excess of end product (e.g., excess acetyl-CoA in the case of PDH) and can also be modulated by ATP/ADP ratios and substrate availability within the mitochondria [25]. In addition to [Ca2 +]mito, increased [Ca2 +]cyt can also increase NADH levels in the mitochondria by stimulating mitochondrial shuttle systems (the glycerol phosphate shuttle [25] and the aspartate/glutamate transporters [75]).
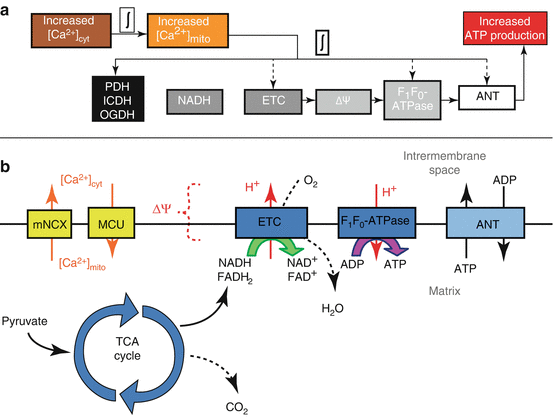

Fig. 5.4
(a) Excitation-energy coupling in airway smooth muscle cells indicating main temporal delays. The delay between [Ca2+]cyt and [Ca2+]mito is estimated to be ~10 s while the delay between [Ca2+]mito and increased ATP production is anticipated to be much faster. (b) ATP production in mitochondria summarized by main processes and intermediates also including the linkage between [Ca2+]cyt and [Ca2+]mito as mediated by Ca2+ uptake by the MCU and Ca2+ release by the mNCX. PDH pyruvate dehydrogenase, ICDH NAD-isocitrate dehydrogenase, OGDH oxoglutarate dehydrogenase, ETC electron transport chain, ΔΨ mitochondrial membrane potential, ANT adenine nucleotide transporter, mNCX mitochondrial Na+/Ca2+ exchanger, MCU mitochondrial Ca2+ uniporter, TCA cycle tricarboxylic acid cycle
The impact of increased NADH is summarized briefly (Fig. 5.4b). NADH donates electrons to the electron transport chain (ETC) within the inner membrane of the mitochondria. As the ETC catalyzes electron flow, H+ is pumped against its concentration gradient out of the mitochondrial matrix. The final stage of the ETC requires O2 to accept electrons (at Complex IV). Therefore, electrons flowing through the ETC results in O2 consumption and, due to H+ pumping, the formation of a proton-motive force (pmf) which has electrical (ΔΨ) and chemical (ΔpH) features. The pmf favors the flow of protons into the mitochondrial matrix. The F1Fo-ATPase (also called Complex V), which is permeable to H+, uses the energy dissipated by pmf-driven proton flow into the matrix to synthesize ATP from ADP and Pi. Synthesized ATP is then transported to the cytosol in exchange for cytosolic ADP by the adenine nucleotide transporter (ANT).
Clearly, mitochondrial ATP production is a multistep process and, therefore, contains many potential regulatory sites upstream and downstream [11, 38, 90]. A recent review [36] outlines a role for Ca2 + to stimulate ATP production that is not solely dependent on NADH increases, but rather affects multiple sites to result in a “balanced activation” of mitochondrial energy production. For example, the impact of [Ca2 +]mito on mitochondrial ATP production is suspected to extend beyond dehydrogenase activation and may involve constituents of the ETC, F1Fo-ATPase, substrate import, as well as others (Fig. 5.4a) [36].
Temporal Linkage Between Cytosolic [Ca2+] and Mitochondrial [Ca2+]
It has been found in many cell types [30, 46, 88], including smooth muscle [18, 24, 27, 70, 102], that an increase in [Ca2 +]cyt is temporally related to an increase in [Ca2 +]mito (Fig. 5.5). Accordingly, an increase in [Ca2 +]cyt is a main step in a multistep cascade, called excitation-contraction coupling (ECC), which causes muscle to generate force or contract in response to agonist stimulation. Given that [Ca2 +]mito can influence mitochondrial ATP production, the spatial and temporal aspects of [Ca2 +]cyt transients, which likely influence [Ca2 +]mito, are anticipated to play an important role in excitation-energy coupling.
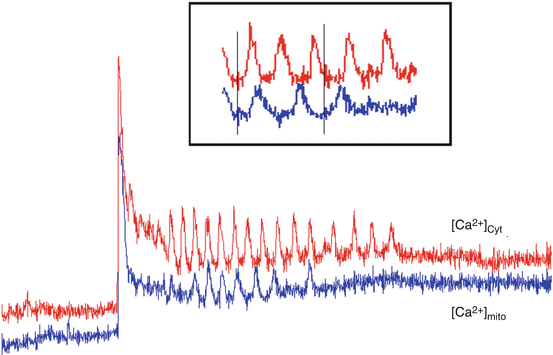





Fig. 5.5
In cells loaded with both fluo-3 (cytosolic Ca2+, [Ca2+]cyt, red) and rhod-2 (mitochondrial Ca2+; [Ca2+]mito, blue), 1 mM ACh-induced [Ca2+]cyt oscillations that were reflected by delayed (~10 s), dampened [Ca2+]mito oscillations. These data suggest that mitochondria take up [Ca2+]cyt during agonist stimulation
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree