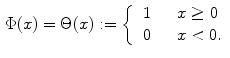Fig. 2.1
Equivalent circuit diagram for the cell membrane. The cell membrane is modeled as a capacitor that is charged to the membrane voltage 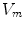 by the Nernst potentials (
by the Nernst potentials (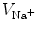 ,…) of different ion species. Variable resistors indicate varying individual permeability of the membrane for each ion species. The current source corresponds to ion transporters in the membrane necessary for ion homeostasis
,…) of different ion species. Variable resistors indicate varying individual permeability of the membrane for each ion species. The current source corresponds to ion transporters in the membrane necessary for ion homeostasis
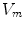 by the Nernst potentials (
by the Nernst potentials (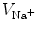 ,…) of different ion species. Variable resistors indicate varying individual permeability of the membrane for each ion species. The current source corresponds to ion transporters in the membrane necessary for ion homeostasis
,…) of different ion species. Variable resistors indicate varying individual permeability of the membrane for each ion species. The current source corresponds to ion transporters in the membrane necessary for ion homeostasis 2.1.1 Single Cell Dynamics
Following Hodgkin’s and Huxleys’s scheme, the electrical behavior of the cell membrane can be modeled by an equivalent circuit as shown in Fig. 2.1: The (impermeable part of the) cell membrane is represented by a capacitor with capacity 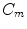 . It can be charged by the accumulation of charge on its two plates (the inner and outer surfaces of the cell membrane) and the potential difference
. It can be charged by the accumulation of charge on its two plates (the inner and outer surfaces of the cell membrane) and the potential difference 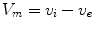 between the intracellular and the extracellular potential is called membrane potential, as explained in Sect. 1.2.1. This happens through passive and active ion channels that determine the permeability and thus the electrical conductivity of the membrane for specific ionic species (
between the intracellular and the extracellular potential is called membrane potential, as explained in Sect. 1.2.1. This happens through passive and active ion channels that determine the permeability and thus the electrical conductivity of the membrane for specific ionic species (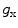 for ion species
for ion species 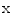 ). Denoting the current through the membrane of ion species
). Denoting the current through the membrane of ion species 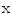 by
by 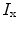 and the charge on the capacitor by
and the charge on the capacitor by 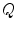 , Kirchhoff’s current law implies that the sum of all currents (through the vertical elements in Fig. 2.1) is zero
, Kirchhoff’s current law implies that the sum of all currents (through the vertical elements in Fig. 2.1) is zero
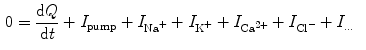
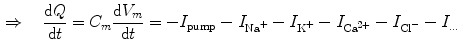
resulting in the above equation for the membrane potential 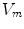 . In the above equation, the convention was used that positive currents point out of the cell, i.e. from intracellular to extracellular, which implies that the charge
. In the above equation, the convention was used that positive currents point out of the cell, i.e. from intracellular to extracellular, which implies that the charge 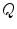 is the one on the intracellular “plate” of the capacitor. The right hand side is sometimes summarized in a term
is the one on the intracellular “plate” of the capacitor. The right hand side is sometimes summarized in a term 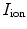 . Each term
. Each term 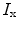 , according to the circuit diagram in Fig. 2.1 is of the form
, according to the circuit diagram in Fig. 2.1 is of the form
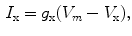
where 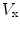 is the reversal potential of the ion species
is the reversal potential of the ion species 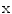 . The dots in Eq. (2.2) and Fig. 2.1 represent additional ion species and dynamic elements that could be included in the model. Due to the existence of multiple ion channel types for the same ionic species, the currents associated with each species in Fig. 2.1 have to be interpreted as net currents and
. The dots in Eq. (2.2) and Fig. 2.1 represent additional ion species and dynamic elements that could be included in the model. Due to the existence of multiple ion channel types for the same ionic species, the currents associated with each species in Fig. 2.1 have to be interpreted as net currents and 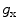 as a net (average) conductivity. Thus, the model could be refined by treating each ion channel type as a separate circuit element. This is indeed done in physiologically detailed models such as the Wang-Sobie model [15], but it is not necessary for the purpose of this thesis.
as a net (average) conductivity. Thus, the model could be refined by treating each ion channel type as a separate circuit element. This is indeed done in physiologically detailed models such as the Wang-Sobie model [15], but it is not necessary for the purpose of this thesis.
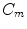 . It can be charged by the accumulation of charge on its two plates (the inner and outer surfaces of the cell membrane) and the potential difference
. It can be charged by the accumulation of charge on its two plates (the inner and outer surfaces of the cell membrane) and the potential difference 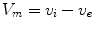 between the intracellular and the extracellular potential is called membrane potential, as explained in Sect. 1.2.1. This happens through passive and active ion channels that determine the permeability and thus the electrical conductivity of the membrane for specific ionic species (
between the intracellular and the extracellular potential is called membrane potential, as explained in Sect. 1.2.1. This happens through passive and active ion channels that determine the permeability and thus the electrical conductivity of the membrane for specific ionic species (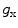 for ion species
for ion species 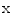 ). Denoting the current through the membrane of ion species
). Denoting the current through the membrane of ion species 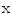 by
by 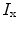 and the charge on the capacitor by
and the charge on the capacitor by 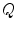 , Kirchhoff’s current law implies that the sum of all currents (through the vertical elements in Fig. 2.1) is zero
, Kirchhoff’s current law implies that the sum of all currents (through the vertical elements in Fig. 2.1) is zero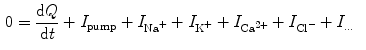
(2.1)
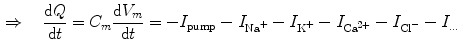
(2.2)
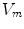 . In the above equation, the convention was used that positive currents point out of the cell, i.e. from intracellular to extracellular, which implies that the charge
. In the above equation, the convention was used that positive currents point out of the cell, i.e. from intracellular to extracellular, which implies that the charge 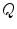 is the one on the intracellular “plate” of the capacitor. The right hand side is sometimes summarized in a term
is the one on the intracellular “plate” of the capacitor. The right hand side is sometimes summarized in a term 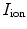 . Each term
. Each term 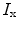 , according to the circuit diagram in Fig. 2.1 is of the form
, according to the circuit diagram in Fig. 2.1 is of the form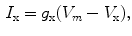
(2.3)
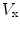 is the reversal potential of the ion species
is the reversal potential of the ion species  . The dots in Eq. (2.2) and Fig. 2.1 represent additional ion species and dynamic elements that could be included in the model. Due to the existence of multiple ion channel types for the same ionic species, the currents associated with each species in Fig. 2.1 have to be interpreted as net currents and
. The dots in Eq. (2.2) and Fig. 2.1 represent additional ion species and dynamic elements that could be included in the model. Due to the existence of multiple ion channel types for the same ionic species, the currents associated with each species in Fig. 2.1 have to be interpreted as net currents and 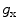 as a net (average) conductivity. Thus, the model could be refined by treating each ion channel type as a separate circuit element. This is indeed done in physiologically detailed models such as the Wang-Sobie model [15], but it is not necessary for the purpose of this thesis.
as a net (average) conductivity. Thus, the model could be refined by treating each ion channel type as a separate circuit element. This is indeed done in physiologically detailed models such as the Wang-Sobie model [15], but it is not necessary for the purpose of this thesis.In contrast, an important aspect that has to be taken into account and that is at the basis of the nonlinear phenomenon of action potential formation is the variability of the conductances 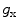 . These are functions of time as well as the quantity gating the channel (membrane potential, individual ion concentrations or mechanical stress, cf. Sect. 1.2.1 and Ref. [16]). As mentioned in the introduction of this chapter, the development of the Hodgkin-Huxley formalism preceded the discovery of the molecular functioning of ion channels. Still, from the measured current traces in voltage clamp experiments, it was already clear that the dynamics of the individual ion conductances can themselves only be modeled by dynamical systems for the so-called gating variables. These describe the transitions between different states of the ion channel or its subunits, the main parameters being the transition rates that are, in turn, determined by the quantity responsible for gating the channel (e.g.,
. These are functions of time as well as the quantity gating the channel (membrane potential, individual ion concentrations or mechanical stress, cf. Sect. 1.2.1 and Ref. [16]). As mentioned in the introduction of this chapter, the development of the Hodgkin-Huxley formalism preceded the discovery of the molecular functioning of ion channels. Still, from the measured current traces in voltage clamp experiments, it was already clear that the dynamics of the individual ion conductances can themselves only be modeled by dynamical systems for the so-called gating variables. These describe the transitions between different states of the ion channel or its subunits, the main parameters being the transition rates that are, in turn, determined by the quantity responsible for gating the channel (e.g., 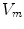 for voltage-gated channels). Depending on the absolute number of channels, a stochastic or deterministic model for the gating variables is required to accurately model the overall membrane conductance for a particular ionic species [17, 18]. As this thesis deals with macroscopic systems only, deterministic dynamics modeled by differential equations will be assumed in the following. In general, each current term in Eq. (2.2) is thus supplemented by a number of additional ordinary differential equations describing its (in-)activation dynamics. The full system of equations describing a single cell electrophysiological model in its most abstract form thus reads
for voltage-gated channels). Depending on the absolute number of channels, a stochastic or deterministic model for the gating variables is required to accurately model the overall membrane conductance for a particular ionic species [17, 18]. As this thesis deals with macroscopic systems only, deterministic dynamics modeled by differential equations will be assumed in the following. In general, each current term in Eq. (2.2) is thus supplemented by a number of additional ordinary differential equations describing its (in-)activation dynamics. The full system of equations describing a single cell electrophysiological model in its most abstract form thus reads
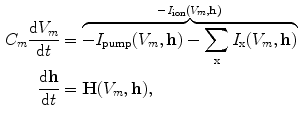
where the vector 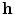 consists of the gating and all further variables necessary to model the individual components (this may also include ion concentrations, etc.). All current electrophysiological cell models have the form of Eq. (2.4) and the number of terms on the right hand side varies with model complexity, either absorbing many summands into one term or splitting some of them up into individual contributions (see Sect. 2.1.6 for details).
consists of the gating and all further variables necessary to model the individual components (this may also include ion concentrations, etc.). All current electrophysiological cell models have the form of Eq. (2.4) and the number of terms on the right hand side varies with model complexity, either absorbing many summands into one term or splitting some of them up into individual contributions (see Sect. 2.1.6 for details).
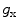 . These are functions of time as well as the quantity gating the channel (membrane potential, individual ion concentrations or mechanical stress, cf. Sect. 1.2.1 and Ref. [16]). As mentioned in the introduction of this chapter, the development of the Hodgkin-Huxley formalism preceded the discovery of the molecular functioning of ion channels. Still, from the measured current traces in voltage clamp experiments, it was already clear that the dynamics of the individual ion conductances can themselves only be modeled by dynamical systems for the so-called gating variables. These describe the transitions between different states of the ion channel or its subunits, the main parameters being the transition rates that are, in turn, determined by the quantity responsible for gating the channel (e.g.,
. These are functions of time as well as the quantity gating the channel (membrane potential, individual ion concentrations or mechanical stress, cf. Sect. 1.2.1 and Ref. [16]). As mentioned in the introduction of this chapter, the development of the Hodgkin-Huxley formalism preceded the discovery of the molecular functioning of ion channels. Still, from the measured current traces in voltage clamp experiments, it was already clear that the dynamics of the individual ion conductances can themselves only be modeled by dynamical systems for the so-called gating variables. These describe the transitions between different states of the ion channel or its subunits, the main parameters being the transition rates that are, in turn, determined by the quantity responsible for gating the channel (e.g., 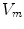 for voltage-gated channels). Depending on the absolute number of channels, a stochastic or deterministic model for the gating variables is required to accurately model the overall membrane conductance for a particular ionic species [17, 18]. As this thesis deals with macroscopic systems only, deterministic dynamics modeled by differential equations will be assumed in the following. In general, each current term in Eq. (2.2) is thus supplemented by a number of additional ordinary differential equations describing its (in-)activation dynamics. The full system of equations describing a single cell electrophysiological model in its most abstract form thus reads
for voltage-gated channels). Depending on the absolute number of channels, a stochastic or deterministic model for the gating variables is required to accurately model the overall membrane conductance for a particular ionic species [17, 18]. As this thesis deals with macroscopic systems only, deterministic dynamics modeled by differential equations will be assumed in the following. In general, each current term in Eq. (2.2) is thus supplemented by a number of additional ordinary differential equations describing its (in-)activation dynamics. The full system of equations describing a single cell electrophysiological model in its most abstract form thus reads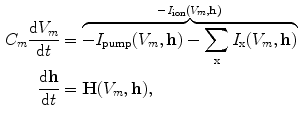
(2.4)
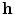 consists of the gating and all further variables necessary to model the individual components (this may also include ion concentrations, etc.). All current electrophysiological cell models have the form of Eq. (2.4) and the number of terms on the right hand side varies with model complexity, either absorbing many summands into one term or splitting some of them up into individual contributions (see Sect. 2.1.6 for details).
consists of the gating and all further variables necessary to model the individual components (this may also include ion concentrations, etc.). All current electrophysiological cell models have the form of Eq. (2.4) and the number of terms on the right hand side varies with model complexity, either absorbing many summands into one term or splitting some of them up into individual contributions (see Sect. 2.1.6 for details).2.1.2 Bi-domain Description of Cardiac Tissue
The single-cell model introduced in Sect. 2.1.1 can be thought of as a description for an average piece of the cell membrane without any spatial extent. In this case, 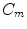 ,
, 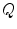 and the current
and the current 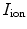 in Eq. (2.4) have to be interpreted as capacitance, charge and current per unit membrane area. This can be used to construct a model of a
in Eq. (2.4) have to be interpreted as capacitance, charge and current per unit membrane area. This can be used to construct a model of a 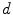 -dimensional domain of cardiac tissue by extending the so-called core conductor model of neuronal cable theory [19], an idea that emerged during efforts in the 1970s to model surface electrocardiograms [20–22]. The resulting mathematical framework is currently viewed as the standard and most accurate model of cardiac tissue as a continuum [23–25]. If an extended slab of cardiac tissue is considered, the intracellular potentials,
-dimensional domain of cardiac tissue by extending the so-called core conductor model of neuronal cable theory [19], an idea that emerged during efforts in the 1970s to model surface electrocardiograms [20–22]. The resulting mathematical framework is currently viewed as the standard and most accurate model of cardiac tissue as a continuum [23–25]. If an extended slab of cardiac tissue is considered, the intracellular potentials, 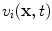 and
and 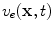 , respectively, become functions of the position
, respectively, become functions of the position 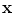 in space, i.e.
in space, i.e. 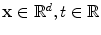 . The idea behind this is that both intracellular and extracellular spaces are defined in the whole tissue domain (thus occupying the same physical space) and have conductivity tensors
. The idea behind this is that both intracellular and extracellular spaces are defined in the whole tissue domain (thus occupying the same physical space) and have conductivity tensors 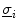 and
and 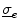 , respectively, that are averaged quantities over multiple cells. The relative volumes of the physical intracellular and extracellular spaces and the geometrical arrangement of cells are implicitly contained in these averaged conductivities, as is the additional resistance introduced by gap junctions in the intracellular domain. The two domains represent spatially extended versions of the capacitor plates considered in the single cell model. Current densities within each domain caused by the corresponding potentials are:
, respectively, that are averaged quantities over multiple cells. The relative volumes of the physical intracellular and extracellular spaces and the geometrical arrangement of cells are implicitly contained in these averaged conductivities, as is the additional resistance introduced by gap junctions in the intracellular domain. The two domains represent spatially extended versions of the capacitor plates considered in the single cell model. Current densities within each domain caused by the corresponding potentials are:
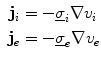
The current densities enter continuity equations for the charge densities 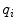 and
and 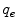 in the intracellular and extracellular domain, respectively. It is assumed that no charge accumulates anywhere in the tissue, such that
in the intracellular and extracellular domain, respectively. It is assumed that no charge accumulates anywhere in the tissue, such that 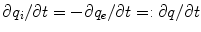 and
and
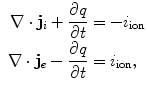
where the lowercase quantities 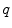 and
and 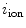 are charge and membrane current per unit volume, respectively. Otherwise, the same sign conventions as in Sect. 2.1.1 apply. The membrane currents appear as sources and sinks for the extracellular and intracellular domain, respectively, as crossing the cell membrane is the only way for charge to leave one of the two domains (in the absence of current injection via electrodes). As the corresponding quantities
are charge and membrane current per unit volume, respectively. Otherwise, the same sign conventions as in Sect. 2.1.1 apply. The membrane currents appear as sources and sinks for the extracellular and intracellular domain, respectively, as crossing the cell membrane is the only way for charge to leave one of the two domains (in the absence of current injection via electrodes). As the corresponding quantities 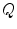 and
and 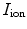 are given per unit membrane area, these quantities have to be converted using the surface-to-volume ratio
are given per unit membrane area, these quantities have to be converted using the surface-to-volume ratio 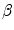 (units: area per volume) which specifies how much membrane surface there is on average for a given volume of tissue. Combining Eqs. (2.5) and (2.6), the Bi-domain equations for the tissue domain
(units: area per volume) which specifies how much membrane surface there is on average for a given volume of tissue. Combining Eqs. (2.5) and (2.6), the Bi-domain equations for the tissue domain 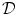 are obtained:
are obtained:
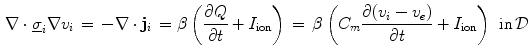
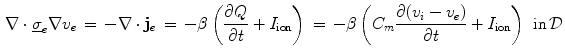
These equations have to be completed by boundary conditions for 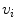 and
and 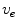 at the boundary
at the boundary 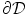 of the tissue domain
of the tissue domain 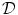 . Assuming the space outside the tissue domain
. Assuming the space outside the tissue domain 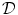 is a mono-domain with conductivity
is a mono-domain with conductivity 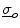 and a corresponding outside potential
and a corresponding outside potential 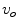 , these boundary conditions are
, these boundary conditions are
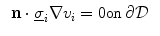
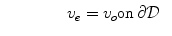
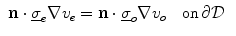
where 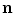 is a local unit vector perpendicular to the boundary
is a local unit vector perpendicular to the boundary 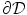 . Equation (2.8a) is a no-flux boundary condition, expressing the fact that the intracellular space ends at the tissue boundary and thus no current in the intracellular domain can cross this boundary. Equations (2.8b) and (2.8c) ensure the continuity of the extracellular potential and currents at the interface between the extracellular space inside the tissue and the mono-domain outside the tissue (e.g., the bath).
. Equation (2.8a) is a no-flux boundary condition, expressing the fact that the intracellular space ends at the tissue boundary and thus no current in the intracellular domain can cross this boundary. Equations (2.8b) and (2.8c) ensure the continuity of the extracellular potential and currents at the interface between the extracellular space inside the tissue and the mono-domain outside the tissue (e.g., the bath).
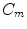 ,
, 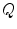 and the current
and the current 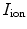 in Eq. (2.4) have to be interpreted as capacitance, charge and current per unit membrane area. This can be used to construct a model of a
in Eq. (2.4) have to be interpreted as capacitance, charge and current per unit membrane area. This can be used to construct a model of a 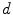 -dimensional domain of cardiac tissue by extending the so-called core conductor model of neuronal cable theory [19], an idea that emerged during efforts in the 1970s to model surface electrocardiograms [20–22]. The resulting mathematical framework is currently viewed as the standard and most accurate model of cardiac tissue as a continuum [23–25]. If an extended slab of cardiac tissue is considered, the intracellular potentials,
-dimensional domain of cardiac tissue by extending the so-called core conductor model of neuronal cable theory [19], an idea that emerged during efforts in the 1970s to model surface electrocardiograms [20–22]. The resulting mathematical framework is currently viewed as the standard and most accurate model of cardiac tissue as a continuum [23–25]. If an extended slab of cardiac tissue is considered, the intracellular potentials, 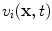 and
and 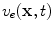 , respectively, become functions of the position
, respectively, become functions of the position 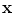 in space, i.e.
in space, i.e. 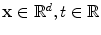 . The idea behind this is that both intracellular and extracellular spaces are defined in the whole tissue domain (thus occupying the same physical space) and have conductivity tensors
. The idea behind this is that both intracellular and extracellular spaces are defined in the whole tissue domain (thus occupying the same physical space) and have conductivity tensors 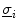 and
and 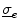 , respectively, that are averaged quantities over multiple cells. The relative volumes of the physical intracellular and extracellular spaces and the geometrical arrangement of cells are implicitly contained in these averaged conductivities, as is the additional resistance introduced by gap junctions in the intracellular domain. The two domains represent spatially extended versions of the capacitor plates considered in the single cell model. Current densities within each domain caused by the corresponding potentials are:
, respectively, that are averaged quantities over multiple cells. The relative volumes of the physical intracellular and extracellular spaces and the geometrical arrangement of cells are implicitly contained in these averaged conductivities, as is the additional resistance introduced by gap junctions in the intracellular domain. The two domains represent spatially extended versions of the capacitor plates considered in the single cell model. Current densities within each domain caused by the corresponding potentials are: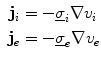
(2.5)
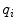 and
and 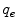 in the intracellular and extracellular domain, respectively. It is assumed that no charge accumulates anywhere in the tissue, such that
in the intracellular and extracellular domain, respectively. It is assumed that no charge accumulates anywhere in the tissue, such that 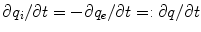 and
and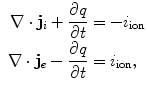
(2.6)
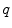 and
and 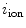 are charge and membrane current per unit volume, respectively. Otherwise, the same sign conventions as in Sect. 2.1.1 apply. The membrane currents appear as sources and sinks for the extracellular and intracellular domain, respectively, as crossing the cell membrane is the only way for charge to leave one of the two domains (in the absence of current injection via electrodes). As the corresponding quantities
are charge and membrane current per unit volume, respectively. Otherwise, the same sign conventions as in Sect. 2.1.1 apply. The membrane currents appear as sources and sinks for the extracellular and intracellular domain, respectively, as crossing the cell membrane is the only way for charge to leave one of the two domains (in the absence of current injection via electrodes). As the corresponding quantities 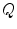 and
and 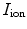 are given per unit membrane area, these quantities have to be converted using the surface-to-volume ratio
are given per unit membrane area, these quantities have to be converted using the surface-to-volume ratio 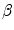 (units: area per volume) which specifies how much membrane surface there is on average for a given volume of tissue. Combining Eqs. (2.5) and (2.6), the Bi-domain equations for the tissue domain
(units: area per volume) which specifies how much membrane surface there is on average for a given volume of tissue. Combining Eqs. (2.5) and (2.6), the Bi-domain equations for the tissue domain 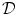 are obtained:
are obtained: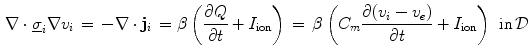
(2.7a)
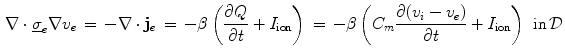
(2.7b)
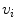 and
and 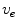 at the boundary
at the boundary 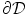 of the tissue domain
of the tissue domain 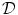 . Assuming the space outside the tissue domain
. Assuming the space outside the tissue domain 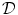 is a mono-domain with conductivity
is a mono-domain with conductivity 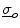 and a corresponding outside potential
and a corresponding outside potential 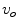 , these boundary conditions are
, these boundary conditions are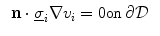
(2.8a)
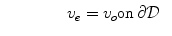
(2.8b)
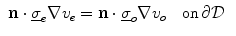
(2.8c)
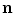 is a local unit vector perpendicular to the boundary
is a local unit vector perpendicular to the boundary 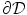 . Equation (2.8a) is a no-flux boundary condition, expressing the fact that the intracellular space ends at the tissue boundary and thus no current in the intracellular domain can cross this boundary. Equations (2.8b) and (2.8c) ensure the continuity of the extracellular potential and currents at the interface between the extracellular space inside the tissue and the mono-domain outside the tissue (e.g., the bath).
. Equation (2.8a) is a no-flux boundary condition, expressing the fact that the intracellular space ends at the tissue boundary and thus no current in the intracellular domain can cross this boundary. Equations (2.8b) and (2.8c) ensure the continuity of the extracellular potential and currents at the interface between the extracellular space inside the tissue and the mono-domain outside the tissue (e.g., the bath).For practical calculations, a different linear combination of the system (2.7) is used which corresponds to a change of variables from 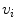 and
and 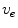 to
to 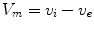 and
and 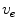 :
:
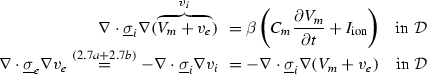 Reordering the terms in both equations yields
Reordering the terms in both equations yields
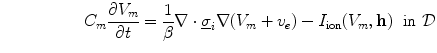
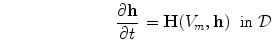
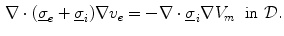
Having been omitted so far, Eq. (2.9b) was reinserted from Eq. (2.4) for completeness. Equation (2.9c) does not contain 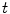 and thus states that the extracellular potential can be determined from the membrane potential at any given instant. In Eq. (2.9a), the term
and thus states that the extracellular potential can be determined from the membrane potential at any given instant. In Eq. (2.9a), the term 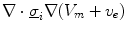 is more favorable than the seemingly simpler
is more favorable than the seemingly simpler 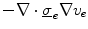 , because in this way, the equation stays valid in the limit
, because in this way, the equation stays valid in the limit 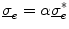 for
for 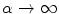 . This will be useful in the next section. For the boundary conditions (2.8), the change of variables can be achieved by replacing
. This will be useful in the next section. For the boundary conditions (2.8), the change of variables can be achieved by replacing 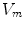 in Eq. (2.8a):
in Eq. (2.8a):
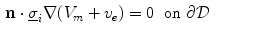
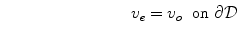
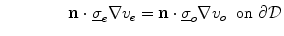
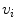 and
and 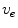 to
to 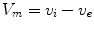 and
and 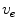 :
: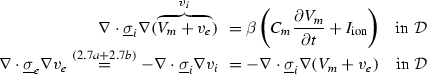
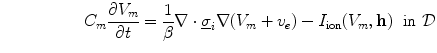
(2.9a)
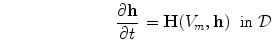
(2.9b)
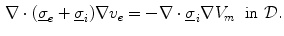
(2.9c)
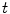 and thus states that the extracellular potential can be determined from the membrane potential at any given instant. In Eq. (2.9a), the term
and thus states that the extracellular potential can be determined from the membrane potential at any given instant. In Eq. (2.9a), the term 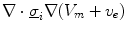 is more favorable than the seemingly simpler
is more favorable than the seemingly simpler 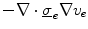 , because in this way, the equation stays valid in the limit
, because in this way, the equation stays valid in the limit 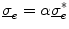 for
for 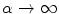 . This will be useful in the next section. For the boundary conditions (2.8), the change of variables can be achieved by replacing
. This will be useful in the next section. For the boundary conditions (2.8), the change of variables can be achieved by replacing 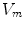 in Eq. (2.8a):
in Eq. (2.8a):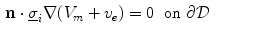
(2.10a)
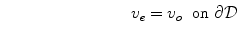
(2.10b)
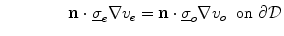
(2.10c)
2.1.3 Mono-domain Descriptions of Cardiac Tissue
For full numerical simulations using the bi-domain equations (2.9), one would have to time-step the membrane potential 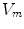 using Eq. (2.9a) from a given present state and calculate the corresponding extracellular potential by solving Eq. (2.9c) for
using Eq. (2.9a) from a given present state and calculate the corresponding extracellular potential by solving Eq. (2.9c) for 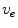 . The latter requires solving a large system of linear equations, an operation that is computationally very costly. Because of this, there exists an approximation that only involves a single partial differential equation (PDE) for
. The latter requires solving a large system of linear equations, an operation that is computationally very costly. Because of this, there exists an approximation that only involves a single partial differential equation (PDE) for 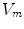 that can be solved by time stepping, the so-called mono-domain equation. Although the mono-domain model is used extensively in the literature and is regarded a valid model in its own right without further justification, it is important to know its connection to the full and more realistic bi-domain formulation. In particular, this is true for understanding the effects of electric fields near tissue boundaries, which is one of the aims of this thesis. In the following two sub-sections, two different ways of deriving the mono-domain equation with different physical interpretation will be presented. When working with a mono-domain equation, one has to ensure that modifications to the equations are consistent with the choice of interpretation.
that can be solved by time stepping, the so-called mono-domain equation. Although the mono-domain model is used extensively in the literature and is regarded a valid model in its own right without further justification, it is important to know its connection to the full and more realistic bi-domain formulation. In particular, this is true for understanding the effects of electric fields near tissue boundaries, which is one of the aims of this thesis. In the following two sub-sections, two different ways of deriving the mono-domain equation with different physical interpretation will be presented. When working with a mono-domain equation, one has to ensure that modifications to the equations are consistent with the choice of interpretation.
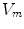 using Eq. (2.9a) from a given present state and calculate the corresponding extracellular potential by solving Eq. (2.9c) for
using Eq. (2.9a) from a given present state and calculate the corresponding extracellular potential by solving Eq. (2.9c) for 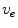 . The latter requires solving a large system of linear equations, an operation that is computationally very costly. Because of this, there exists an approximation that only involves a single partial differential equation (PDE) for
. The latter requires solving a large system of linear equations, an operation that is computationally very costly. Because of this, there exists an approximation that only involves a single partial differential equation (PDE) for 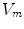 that can be solved by time stepping, the so-called mono-domain equation. Although the mono-domain model is used extensively in the literature and is regarded a valid model in its own right without further justification, it is important to know its connection to the full and more realistic bi-domain formulation. In particular, this is true for understanding the effects of electric fields near tissue boundaries, which is one of the aims of this thesis. In the following two sub-sections, two different ways of deriving the mono-domain equation with different physical interpretation will be presented. When working with a mono-domain equation, one has to ensure that modifications to the equations are consistent with the choice of interpretation.
that can be solved by time stepping, the so-called mono-domain equation. Although the mono-domain model is used extensively in the literature and is regarded a valid model in its own right without further justification, it is important to know its connection to the full and more realistic bi-domain formulation. In particular, this is true for understanding the effects of electric fields near tissue boundaries, which is one of the aims of this thesis. In the following two sub-sections, two different ways of deriving the mono-domain equation with different physical interpretation will be presented. When working with a mono-domain equation, one has to ensure that modifications to the equations are consistent with the choice of interpretation.2.1.3.1 Neglecting the Extracellular Potential
Assume a very well-conducting extracellular space,2 i.e. 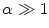 for
for 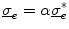 . In the limit
. In the limit 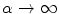 , Eq. (2.9c) reduces to
, Eq. (2.9c) reduces to 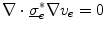 . This means that for large
. This means that for large 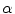 the source term for the extracellular potential becomes negligible and one possible form of solution is
the source term for the extracellular potential becomes negligible and one possible form of solution is 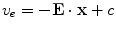 with some fixed electric field vector
with some fixed electric field vector 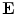 and an arbitrary constant
and an arbitrary constant 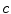 (if boundary conditions (2.10b) and (2.10c) permit).3 For this solution, it has to be assumed that
(if boundary conditions (2.10b) and (2.10c) permit).3 For this solution, it has to be assumed that 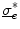 is spatially constant. If we assume the extracellular space is insulated (
is spatially constant. If we assume the extracellular space is insulated (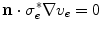 ) or grounded (
) or grounded (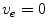 ) on
) on 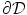 , this solution reduces even further to
, this solution reduces even further to 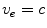 or
or 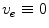 , respectively. In contrast, Eq. (2.9a) is still valid. The mono-domain equation in this scenario therefore is
, respectively. In contrast, Eq. (2.9a) is still valid. The mono-domain equation in this scenario therefore is
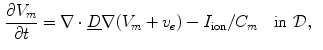
where the diffusion tensor is given by 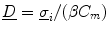 and
and 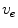 is merely a parameter for the problem, which is usually set to zero following the line of thoughts above. To make this problem well-defined, the boundary condition (2.10a) is sufficient:
is merely a parameter for the problem, which is usually set to zero following the line of thoughts above. To make this problem well-defined, the boundary condition (2.10a) is sufficient:
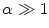 for
for 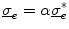 . In the limit
. In the limit 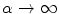 , Eq. (2.9c) reduces to
, Eq. (2.9c) reduces to 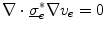 . This means that for large
. This means that for large 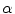 the source term for the extracellular potential becomes negligible and one possible form of solution is
the source term for the extracellular potential becomes negligible and one possible form of solution is 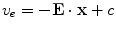 with some fixed electric field vector
with some fixed electric field vector 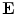 and an arbitrary constant
and an arbitrary constant 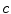 (if boundary conditions (2.10b) and (2.10c) permit).3 For this solution, it has to be assumed that
(if boundary conditions (2.10b) and (2.10c) permit).3 For this solution, it has to be assumed that 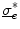 is spatially constant. If we assume the extracellular space is insulated (
is spatially constant. If we assume the extracellular space is insulated (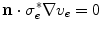 ) or grounded (
) or grounded (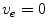 ) on
) on 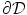 , this solution reduces even further to
, this solution reduces even further to 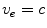 or
or 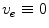 , respectively. In contrast, Eq. (2.9a) is still valid. The mono-domain equation in this scenario therefore is
, respectively. In contrast, Eq. (2.9a) is still valid. The mono-domain equation in this scenario therefore is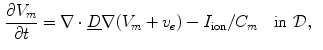
(2.11)
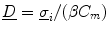 and
and 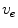 is merely a parameter for the problem, which is usually set to zero following the line of thoughts above. To make this problem well-defined, the boundary condition (2.10a) is sufficient:
is merely a parameter for the problem, which is usually set to zero following the line of thoughts above. To make this problem well-defined, the boundary condition (2.10a) is sufficient: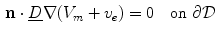
(2.12)
2.1.3.2 Equivalent Mono-domain Description
In Sect. 2.1.3.1, a mono-domain formulation of the bi-domain model was obtained by changing the physics of the problem. The extent to which the dynamics is altered can be significantly reduced in the case were the intracellular and extracellular conductivity tensors are scaled versions of the same tensor: 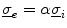 . In this case, Eq. (2.7b) can be subtracted from Eq. (2.7a):
. In this case, Eq. (2.7b) can be subtracted from Eq. (2.7a):
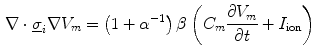 Rearranging for
Rearranging for 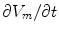 yields the mono-domain equation
yields the mono-domain equation
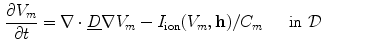
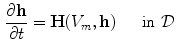
where now ![$${\underline{D}}={\underline{\sigma }}_i/[\beta C_m(1+\alpha ^{-1})]$$](/wp-content/uploads/2016/11/A328193_1_En_2_Chapter_IEq83.gif) . In the limit
. In the limit 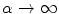 , the definition of
, the definition of 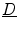 is equal to that in Eq. (2.11). Similarly, the
is equal to that in Eq. (2.11). Similarly, the 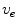 term in Eq. (2.11) becomes irrelevant if
term in Eq. (2.11) becomes irrelevant if 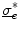 is a scaled
is a scaled 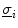 , because then
, because then 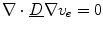 follows from
follows from 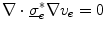 . Equations (2.11) and (2.13) are thus consistent in the sense that they are equivalent when the assumptions for both mono-domain descriptions are fulfilled.
. Equations (2.11) and (2.13) are thus consistent in the sense that they are equivalent when the assumptions for both mono-domain descriptions are fulfilled.
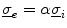 . In this case, Eq. (2.7b) can be subtracted from Eq. (2.7a):
. In this case, Eq. (2.7b) can be subtracted from Eq. (2.7a):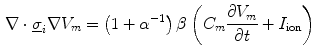
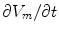 yields the mono-domain equation
yields the mono-domain equation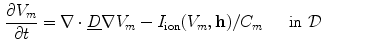
(2.13a)
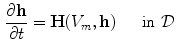
(2.13b)
![$${\underline{D}}={\underline{\sigma }}_i/[\beta C_m(1+\alpha ^{-1})]$$](/wp-content/uploads/2016/11/A328193_1_En_2_Chapter_IEq83.gif) . In the limit
. In the limit  , the definition of
, the definition of  is equal to that in Eq. (2.11). Similarly, the
is equal to that in Eq. (2.11). Similarly, the 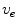 term in Eq. (2.11) becomes irrelevant if
term in Eq. (2.11) becomes irrelevant if 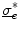 is a scaled
is a scaled 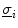 , because then
, because then 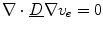 follows from
follows from 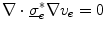 . Equations (2.11) and (2.13) are thus consistent in the sense that they are equivalent when the assumptions for both mono-domain descriptions are fulfilled.
. Equations (2.11) and (2.13) are thus consistent in the sense that they are equivalent when the assumptions for both mono-domain descriptions are fulfilled.Note that the mono-domain description (2.13) is completely equivalent to the full bi-domain model, but numerically cheap compared to Eq. (2.9). Consequently, for the case 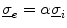 , numerical simulation of the bi-domain model is usually superfluous. There is, however, one caveat: from the set of boundary conditions (2.10), no boundary condition for the membrane potential alone can be derived. Also, unlike in Eq. (2.11),
, numerical simulation of the bi-domain model is usually superfluous. There is, however, one caveat: from the set of boundary conditions (2.10), no boundary condition for the membrane potential alone can be derived. Also, unlike in Eq. (2.11), 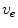 is not decoupled from the membrane potential dynamics and so Eq. (2.10a) cannot be enforced unless
is not decoupled from the membrane potential dynamics and so Eq. (2.10a) cannot be enforced unless 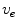 is calculated, which would defeat the original purpose of a mono-domain formulation. The usual (somewhat nonphysical) solution to this dilemma is to apply the ad-hoc no-flux boundary condition
is calculated, which would defeat the original purpose of a mono-domain formulation. The usual (somewhat nonphysical) solution to this dilemma is to apply the ad-hoc no-flux boundary condition
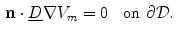
This is sufficient for modeling the dynamics inside a tissue domain  , where the boundary of the domain is not meant to be a physical part of the system but rather a computational necessity. However, it is only a valid simplification, if one can rule out any influence of the boundary condition on the effects one wants to study. Sometimes, the no-flux boundary condition is physically justified, for example, if the extracellular space is known to be insulated electrically at the tissue boundary. However, in particular in this thesis, investigating effects at the boundaries of the tissue due to the conductive connection of the extracellular space to the surrounding environment is the original purpose of the modeling. In this case, an alternative solution is to assume that
, where the boundary of the domain is not meant to be a physical part of the system but rather a computational necessity. However, it is only a valid simplification, if one can rule out any influence of the boundary condition on the effects one wants to study. Sometimes, the no-flux boundary condition is physically justified, for example, if the extracellular space is known to be insulated electrically at the tissue boundary. However, in particular in this thesis, investigating effects at the boundaries of the tissue due to the conductive connection of the extracellular space to the surrounding environment is the original purpose of the modeling. In this case, an alternative solution is to assume that  and the outside conductivity
and the outside conductivity  are large, which decouples the corresponding potentials from the dynamics of the membrane potential and makes them parameters as seen for Eq. (2.11). This way, an extracellular or outside potential (e.g., a uniform electric field) can be assumed rather than calculated, which makes it possible to use Eq. (2.10a) itself or a boundary condition obtained by subtracting Eq. (2.10c) from Eq. (2.10a):
are large, which decouples the corresponding potentials from the dynamics of the membrane potential and makes them parameters as seen for Eq. (2.11). This way, an extracellular or outside potential (e.g., a uniform electric field) can be assumed rather than calculated, which makes it possible to use Eq. (2.10a) itself or a boundary condition obtained by subtracting Eq. (2.10c) from Eq. (2.10a):
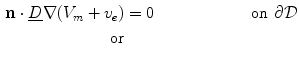
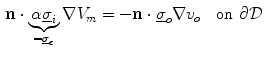
The second boundary condition (2.16) will be used in Sect. 3.2 to study the effect of electric fields near boundaries of the tissue. As for the bi-domain model (2.9), the mono-domain equation (2.13) has to be supplemented by a concrete model  for the local variables
for the local variables 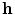 and the corresponding ionic currents
and the corresponding ionic currents 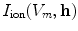 . The models used in this thesis will be introduced in Sect. 2.1.6.
. The models used in this thesis will be introduced in Sect. 2.1.6.
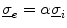 , numerical simulation of the bi-domain model is usually superfluous. There is, however, one caveat: from the set of boundary conditions (2.10), no boundary condition for the membrane potential alone can be derived. Also, unlike in Eq. (2.11),
, numerical simulation of the bi-domain model is usually superfluous. There is, however, one caveat: from the set of boundary conditions (2.10), no boundary condition for the membrane potential alone can be derived. Also, unlike in Eq. (2.11), 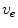 is not decoupled from the membrane potential dynamics and so Eq. (2.10a) cannot be enforced unless
is not decoupled from the membrane potential dynamics and so Eq. (2.10a) cannot be enforced unless 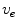 is calculated, which would defeat the original purpose of a mono-domain formulation. The usual (somewhat nonphysical) solution to this dilemma is to apply the ad-hoc no-flux boundary condition
is calculated, which would defeat the original purpose of a mono-domain formulation. The usual (somewhat nonphysical) solution to this dilemma is to apply the ad-hoc no-flux boundary condition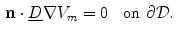
(2.14)
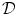 , where the boundary of the domain is not meant to be a physical part of the system but rather a computational necessity. However, it is only a valid simplification, if one can rule out any influence of the boundary condition on the effects one wants to study. Sometimes, the no-flux boundary condition is physically justified, for example, if the extracellular space is known to be insulated electrically at the tissue boundary. However, in particular in this thesis, investigating effects at the boundaries of the tissue due to the conductive connection of the extracellular space to the surrounding environment is the original purpose of the modeling. In this case, an alternative solution is to assume that
, where the boundary of the domain is not meant to be a physical part of the system but rather a computational necessity. However, it is only a valid simplification, if one can rule out any influence of the boundary condition on the effects one wants to study. Sometimes, the no-flux boundary condition is physically justified, for example, if the extracellular space is known to be insulated electrically at the tissue boundary. However, in particular in this thesis, investigating effects at the boundaries of the tissue due to the conductive connection of the extracellular space to the surrounding environment is the original purpose of the modeling. In this case, an alternative solution is to assume that 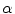 and the outside conductivity
and the outside conductivity 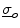 are large, which decouples the corresponding potentials from the dynamics of the membrane potential and makes them parameters as seen for Eq. (2.11). This way, an extracellular or outside potential (e.g., a uniform electric field) can be assumed rather than calculated, which makes it possible to use Eq. (2.10a) itself or a boundary condition obtained by subtracting Eq. (2.10c) from Eq. (2.10a):
are large, which decouples the corresponding potentials from the dynamics of the membrane potential and makes them parameters as seen for Eq. (2.11). This way, an extracellular or outside potential (e.g., a uniform electric field) can be assumed rather than calculated, which makes it possible to use Eq. (2.10a) itself or a boundary condition obtained by subtracting Eq. (2.10c) from Eq. (2.10a):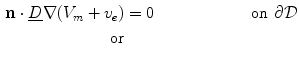
(2.15)
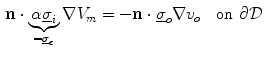
(2.16)
 for the local variables
for the local variables 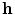 and the corresponding ionic currents
and the corresponding ionic currents 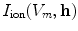 . The models used in this thesis will be introduced in Sect. 2.1.6.
. The models used in this thesis will be introduced in Sect. 2.1.6.2.1.4 Anisotropy
Although all simulations in this thesis are carried out assuming isotropic diffusion, for completeness of the mathematical framework, the construction of the corresponding tensors for the specific requirements of cardiac tissue shall be mentioned here briefly: The anisotropic conductivity of cardiac tissue due to the fiber orientation and sheet structure of the muscle (see Sect. 1.3) can be implemented in the bi-domain and in the mono-domain model by choosing the diffusion tensor 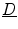 or equivalently the conductivity tensors.
or equivalently the conductivity tensors. 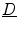 can be constructed from its three eigenvectors, each of which represents a direction in which a potential gradient leads to a current density in the same direction, with a conductivity equal to the corresponding eigenvalue. The fiber orientation determines one of these directions, the other two are uniquely defined by the normal vector of the laminar sheets (the remaining vector thus corresponds to the direction perpendicular to the fibers within the sheet). These three eigenvectors form an orthonormal basis of
can be constructed from its three eigenvectors, each of which represents a direction in which a potential gradient leads to a current density in the same direction, with a conductivity equal to the corresponding eigenvalue. The fiber orientation determines one of these directions, the other two are uniquely defined by the normal vector of the laminar sheets (the remaining vector thus corresponds to the direction perpendicular to the fibers within the sheet). These three eigenvectors form an orthonormal basis of 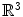 , implying that
, implying that 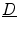 must be a real, symmetric matrix. Using these properties, the entire tensor
must be a real, symmetric matrix. Using these properties, the entire tensor 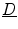 is determined by two unit vectors in space defining the fiber direction
is determined by two unit vectors in space defining the fiber direction 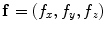 and the direction normal to the sheet plane
and the direction normal to the sheet plane 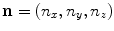 and by diffusion constants
and by diffusion constants  along the fibers,
along the fibers,  perpendicular to the fibers (within the sheet) and
perpendicular to the fibers (within the sheet) and 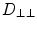 normal to the sheets (see Eq. 17 in [25]):
normal to the sheets (see Eq. 17 in [25]):
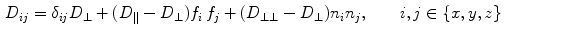
A common simplification is to ignore the sheet structure and thus assume 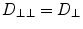 , which eliminates one of the terms in Eq. (2.17). Note also that, in general, both the directions and diffusion constants may vary spatially.
, which eliminates one of the terms in Eq. (2.17). Note also that, in general, both the directions and diffusion constants may vary spatially.
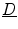 or equivalently the conductivity tensors.
or equivalently the conductivity tensors. 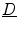 can be constructed from its three eigenvectors, each of which represents a direction in which a potential gradient leads to a current density in the same direction, with a conductivity equal to the corresponding eigenvalue. The fiber orientation determines one of these directions, the other two are uniquely defined by the normal vector of the laminar sheets (the remaining vector thus corresponds to the direction perpendicular to the fibers within the sheet). These three eigenvectors form an orthonormal basis of
can be constructed from its three eigenvectors, each of which represents a direction in which a potential gradient leads to a current density in the same direction, with a conductivity equal to the corresponding eigenvalue. The fiber orientation determines one of these directions, the other two are uniquely defined by the normal vector of the laminar sheets (the remaining vector thus corresponds to the direction perpendicular to the fibers within the sheet). These three eigenvectors form an orthonormal basis of  , implying that
, implying that 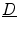 must be a real, symmetric matrix. Using these properties, the entire tensor
must be a real, symmetric matrix. Using these properties, the entire tensor 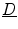 is determined by two unit vectors in space defining the fiber direction
is determined by two unit vectors in space defining the fiber direction 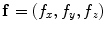 and the direction normal to the sheet plane
and the direction normal to the sheet plane 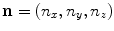 and by diffusion constants
and by diffusion constants  along the fibers,
along the fibers,  perpendicular to the fibers (within the sheet) and
perpendicular to the fibers (within the sheet) and 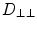 normal to the sheets (see Eq. 17 in [25]):
normal to the sheets (see Eq. 17 in [25]):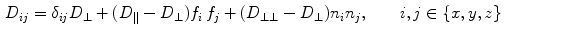
(2.17)
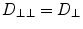 , which eliminates one of the terms in Eq. (2.17). Note also that, in general, both the directions and diffusion constants may vary spatially.
, which eliminates one of the terms in Eq. (2.17). Note also that, in general, both the directions and diffusion constants may vary spatially.The so-called anisotropy ratio is defined as the quotient 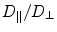 . In the bi-domain equations, the two conductivity tensors
. In the bi-domain equations, the two conductivity tensors 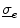 and
and 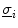 can be chosen independently. While the fiber orientation for both is the same, because it is given by the geometrical arrangement of the cells, the anisotropy ratio can be different. The case of equal anisotropy ratio is the one considered in the mono-domain approximation of Sect. 2.1.3.2.
can be chosen independently. While the fiber orientation for both is the same, because it is given by the geometrical arrangement of the cells, the anisotropy ratio can be different. The case of equal anisotropy ratio is the one considered in the mono-domain approximation of Sect. 2.1.3.2.
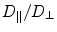 . In the bi-domain equations, the two conductivity tensors
. In the bi-domain equations, the two conductivity tensors 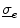 and
and 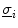 can be chosen independently. While the fiber orientation for both is the same, because it is given by the geometrical arrangement of the cells, the anisotropy ratio can be different. The case of equal anisotropy ratio is the one considered in the mono-domain approximation of Sect. 2.1.3.2.
can be chosen independently. While the fiber orientation for both is the same, because it is given by the geometrical arrangement of the cells, the anisotropy ratio can be different. The case of equal anisotropy ratio is the one considered in the mono-domain approximation of Sect. 2.1.3.2.2.1.5 The Phase-Field Method
As outlined in Sect. 2.1.3, boundary conditions constitute an important part of any problem described by a PDE on a spatial domain  . It was mentioned that a widely-used boundary condition for mono-domain cardiac models is no-flux. Another possibility which was derived for the case of a predetermined extracellular/outside potential is that of Eq. (2.16) in the same section. Both boundary conditions are of the Neumann type, i.e. they fix the normal fluxes
. It was mentioned that a widely-used boundary condition for mono-domain cardiac models is no-flux. Another possibility which was derived for the case of a predetermined extracellular/outside potential is that of Eq. (2.16) in the same section. Both boundary conditions are of the Neumann type, i.e. they fix the normal fluxes 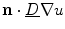 on the boundary
on the boundary  . As will be shown in Sect. 2.2.3, for a finite-difference numerical scheme, no-flux boundary conditions are straightforward to implement, if the boundaries of the domain
. As will be shown in Sect. 2.2.3, for a finite-difference numerical scheme, no-flux boundary conditions are straightforward to implement, if the boundaries of the domain 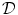 are parallel to the coordinate axes, e.g., rectangles in cartesian coordinates or (fractional) annuli in polar coordinates. For arbitrarily shaped domains
are parallel to the coordinate axes, e.g., rectangles in cartesian coordinates or (fractional) annuli in polar coordinates. For arbitrarily shaped domains 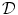 , there is no such natural way of imposing zero flux on the domain boundary. In this case, one usually resorts to more complex and computationally intensive numerical schemes like finite-volume or finite-element methods (see Sect. 6.3 of Ref. [25] and references therein).
, there is no such natural way of imposing zero flux on the domain boundary. In this case, one usually resorts to more complex and computationally intensive numerical schemes like finite-volume or finite-element methods (see Sect. 6.3 of Ref. [25] and references therein).
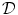 . It was mentioned that a widely-used boundary condition for mono-domain cardiac models is no-flux. Another possibility which was derived for the case of a predetermined extracellular/outside potential is that of Eq. (2.16) in the same section. Both boundary conditions are of the Neumann type, i.e. they fix the normal fluxes
. It was mentioned that a widely-used boundary condition for mono-domain cardiac models is no-flux. Another possibility which was derived for the case of a predetermined extracellular/outside potential is that of Eq. (2.16) in the same section. Both boundary conditions are of the Neumann type, i.e. they fix the normal fluxes 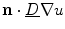 on the boundary
on the boundary 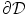 . As will be shown in Sect. 2.2.3, for a finite-difference numerical scheme, no-flux boundary conditions are straightforward to implement, if the boundaries of the domain
. As will be shown in Sect. 2.2.3, for a finite-difference numerical scheme, no-flux boundary conditions are straightforward to implement, if the boundaries of the domain 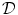 are parallel to the coordinate axes, e.g., rectangles in cartesian coordinates or (fractional) annuli in polar coordinates. For arbitrarily shaped domains
are parallel to the coordinate axes, e.g., rectangles in cartesian coordinates or (fractional) annuli in polar coordinates. For arbitrarily shaped domains 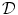 , there is no such natural way of imposing zero flux on the domain boundary. In this case, one usually resorts to more complex and computationally intensive numerical schemes like finite-volume or finite-element methods (see Sect. 6.3 of Ref. [25] and references therein).
, there is no such natural way of imposing zero flux on the domain boundary. In this case, one usually resorts to more complex and computationally intensive numerical schemes like finite-volume or finite-element methods (see Sect. 6.3 of Ref. [25] and references therein).In Ref. [26], Fenton et al. introduce a phase-field method to impose no-flux boundary conditions on arbitrary geometries using finite differences on a simple (e.g., rectangular) computational domain 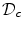 which contains the actual physical domain
which contains the actual physical domain 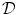 . In the following, this method will be explained in detail and extended to arbitrary Neumann boundary conditions of the type of Eq. (2.16). Furthermore, mathematical improvements to the convergence proof will enable a better assessment of the method’s numerical accuracy. The generalized method will be used extensively in Sect. 3.2 to study the effect of electric fields at boundaries of curved tissue domains.
. In the following, this method will be explained in detail and extended to arbitrary Neumann boundary conditions of the type of Eq. (2.16). Furthermore, mathematical improvements to the convergence proof will enable a better assessment of the method’s numerical accuracy. The generalized method will be used extensively in Sect. 3.2 to study the effect of electric fields at boundaries of curved tissue domains.
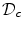 which contains the actual physical domain
which contains the actual physical domain 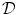 . In the following, this method will be explained in detail and extended to arbitrary Neumann boundary conditions of the type of Eq. (2.16). Furthermore, mathematical improvements to the convergence proof will enable a better assessment of the method’s numerical accuracy. The generalized method will be used extensively in Sect. 3.2 to study the effect of electric fields at boundaries of curved tissue domains.
. In the following, this method will be explained in detail and extended to arbitrary Neumann boundary conditions of the type of Eq. (2.16). Furthermore, mathematical improvements to the convergence proof will enable a better assessment of the method’s numerical accuracy. The generalized method will be used extensively in Sect. 3.2 to study the effect of electric fields at boundaries of curved tissue domains.2.1.5.1 Description of the Method
The phase-field method is based on defining a phase field 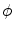 , which is a smoothed version of the characteristic function of
, which is a smoothed version of the characteristic function of 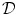 , i.e.
, i.e. 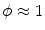 inside the domain
inside the domain 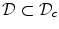 and
and 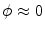 otherwise, with a smooth transition in between. In this thesis, a different dynamical system than suggested in Ref. [26] shall be used for obtaining
otherwise, with a smooth transition in between. In this thesis, a different dynamical system than suggested in Ref. [26] shall be used for obtaining 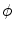 from the sharp, original characteristic function
from the sharp, original characteristic function 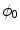 :
:
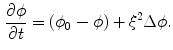
In this equation, 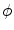 approaches a smooth phase field for
approaches a smooth phase field for 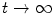 , which stays close to
, which stays close to 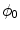 and has a diffusive boundary with a characteristic length scale
and has a diffusive boundary with a characteristic length scale 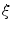 of the resulting transition at the interface between
of the resulting transition at the interface between 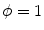 and
and 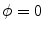 . It does not suffer from the stability issues in higher dimensions mentioned in [26] for the double-well potential method defined therein. Hence, any method that finds the equilibrium of Eq. (2.18) may be used instead of explicit time-stepping. In the following, this steady-state solution will be referred to as
. It does not suffer from the stability issues in higher dimensions mentioned in [26] for the double-well potential method defined therein. Hence, any method that finds the equilibrium of Eq. (2.18) may be used instead of explicit time-stepping. In the following, this steady-state solution will be referred to as 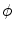 . An example for
. An example for 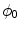 and the resulting
and the resulting 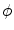 is depicted in Fig. 2.2a, b respectively. One property that will prove to be important for the line of thoughts below is that the normal slope of
is depicted in Fig. 2.2a, b respectively. One property that will prove to be important for the line of thoughts below is that the normal slope of 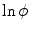 decreases rapidly and monotonically within the interface region (in the outward direction) until reaching an approximately constant value on the order of
decreases rapidly and monotonically within the interface region (in the outward direction) until reaching an approximately constant value on the order of 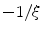 , as shown in Fig. 2.2c. Hence, at large normal distances from the interface,
, as shown in Fig. 2.2c. Hence, at large normal distances from the interface, 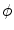 decays approximately exponentially and
decays approximately exponentially and 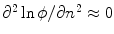 . As illustrated in Fig. 2.2d, the normal direction is defined by the direction of the gradient
. As illustrated in Fig. 2.2d, the normal direction is defined by the direction of the gradient 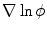 itself.
itself.
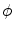 , which is a smoothed version of the characteristic function of
, which is a smoothed version of the characteristic function of 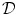 , i.e.
, i.e. 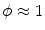 inside the domain
inside the domain 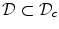 and
and 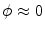 otherwise, with a smooth transition in between. In this thesis, a different dynamical system than suggested in Ref. [26] shall be used for obtaining
otherwise, with a smooth transition in between. In this thesis, a different dynamical system than suggested in Ref. [26] shall be used for obtaining 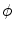 from the sharp, original characteristic function
from the sharp, original characteristic function 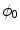 :
: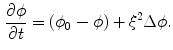
(2.18)
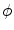 approaches a smooth phase field for
approaches a smooth phase field for 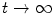 , which stays close to
, which stays close to 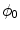 and has a diffusive boundary with a characteristic length scale
and has a diffusive boundary with a characteristic length scale 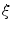 of the resulting transition at the interface between
of the resulting transition at the interface between 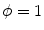 and
and 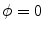 . It does not suffer from the stability issues in higher dimensions mentioned in [26] for the double-well potential method defined therein. Hence, any method that finds the equilibrium of Eq. (2.18) may be used instead of explicit time-stepping. In the following, this steady-state solution will be referred to as
. It does not suffer from the stability issues in higher dimensions mentioned in [26] for the double-well potential method defined therein. Hence, any method that finds the equilibrium of Eq. (2.18) may be used instead of explicit time-stepping. In the following, this steady-state solution will be referred to as 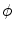 . An example for
. An example for 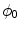 and the resulting
and the resulting 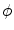 is depicted in Fig. 2.2a, b respectively. One property that will prove to be important for the line of thoughts below is that the normal slope of
is depicted in Fig. 2.2a, b respectively. One property that will prove to be important for the line of thoughts below is that the normal slope of 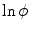 decreases rapidly and monotonically within the interface region (in the outward direction) until reaching an approximately constant value on the order of
decreases rapidly and monotonically within the interface region (in the outward direction) until reaching an approximately constant value on the order of 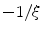 , as shown in Fig. 2.2c. Hence, at large normal distances from the interface,
, as shown in Fig. 2.2c. Hence, at large normal distances from the interface, 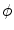 decays approximately exponentially and
decays approximately exponentially and 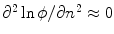 . As illustrated in Fig. 2.2d, the normal direction is defined by the direction of the gradient
. As illustrated in Fig. 2.2d, the normal direction is defined by the direction of the gradient 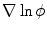 itself.
itself.
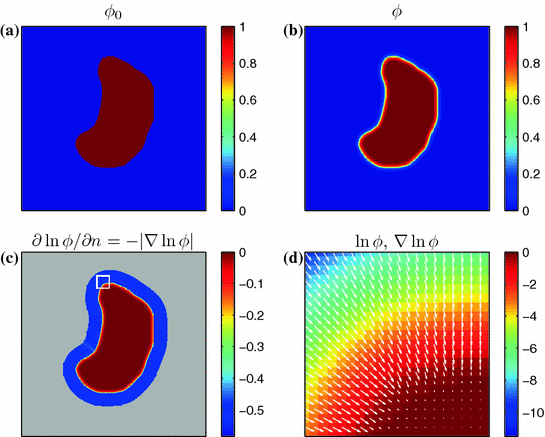
Fig. 2.2
Phase field behavior. a Initial binary phase field 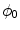 , i.e. the characteristic function of
, i.e. the characteristic function of 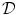 . b Steady-state solution of Eq. (2.18) with
. b Steady-state solution of Eq. (2.18) with 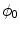 from (a) and
from (a) and 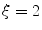 . c
. c 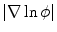 which is equal to
which is equal to 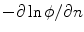 if one defines the normal vector
if one defines the normal vector 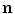 to be anti-parallel to
to be anti-parallel to 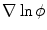 . The logarithmic normal derivative increases quickly from 0 inside
. The logarithmic normal derivative increases quickly from 0 inside 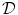 to an approximately constant value
to an approximately constant value 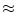
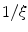 outside
outside 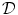 . d
. d 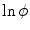 shown as a color plot and the corresponding gradient shown as arrows for the region indicated by a white rectangle in (c)
shown as a color plot and the corresponding gradient shown as arrows for the region indicated by a white rectangle in (c)
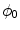 , i.e. the characteristic function of
, i.e. the characteristic function of 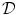 . b Steady-state solution of Eq. (2.18) with
. b Steady-state solution of Eq. (2.18) with 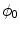 from (a) and
from (a) and 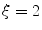 . c
. c 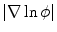 which is equal to
which is equal to 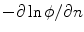 if one defines the normal vector
if one defines the normal vector 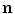 to be anti-parallel to
to be anti-parallel to 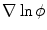 . The logarithmic normal derivative increases quickly from 0 inside
. The logarithmic normal derivative increases quickly from 0 inside 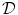 to an approximately constant value
to an approximately constant value 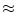
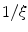 outside
outside 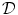 . d
. d 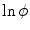 shown as a color plot and the corresponding gradient shown as arrows for the region indicated by a white rectangle in (c)
shown as a color plot and the corresponding gradient shown as arrows for the region indicated by a white rectangle in (c)The phase field method then consists of substituting the original diffusion term (e.g., in Eq. (2.13)) by a modified term that involves the phase field 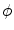 :
:
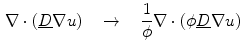
The resulting PDE after the substitution is assumed to be defined on the whole domain 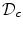 , but only the part of the solution in
, but only the part of the solution in 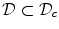 is taken to have physical meaning. Fenton et al. present a mathematical argument in Ref. [26] for a one-dimensional tissue domain which suggests that the substitution (2.19) for
is taken to have physical meaning. Fenton et al. present a mathematical argument in Ref. [26] for a one-dimensional tissue domain which suggests that the substitution (2.19) for 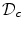 leads to a solution in
leads to a solution in 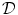 that obeys a no-flux boundary condition
that obeys a no-flux boundary condition
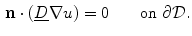
A similar proof for higher dimensions based on the same idea was provided in Ref. [27]. In the following, this idea and its shortcomings in terms of the necessary mathematical assumptions will be presented and an argument will be given how these deficits may be resolved.
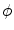 :
: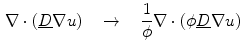
(2.19)
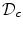 , but only the part of the solution in
, but only the part of the solution in 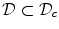 is taken to have physical meaning. Fenton et al. present a mathematical argument in Ref. [26] for a one-dimensional tissue domain which suggests that the substitution (2.19) for
is taken to have physical meaning. Fenton et al. present a mathematical argument in Ref. [26] for a one-dimensional tissue domain which suggests that the substitution (2.19) for 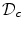 leads to a solution in
leads to a solution in 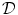 that obeys a no-flux boundary condition
that obeys a no-flux boundary condition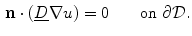
(2.20)
2.1.5.2 Original Convergence Proof
Omitting any additional non-spatial degrees of freedom for the reaction term, the general PDE for a reaction-diffusion system with the replacement of Eq. (2.19) is
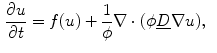
where 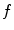 is assumed to be bounded for bounded
is assumed to be bounded for bounded 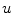 . The multi-dimensional equivalent of the mathematical argument given in [26] starts by integrating Eq. (2.21) over a small volume
. The multi-dimensional equivalent of the mathematical argument given in [26] starts by integrating Eq. (2.21) over a small volume 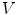 across the boundary
across the boundary  , which yields
, which yields
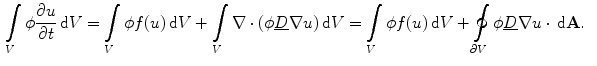
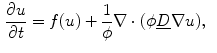
(2.21)
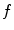 is assumed to be bounded for bounded
is assumed to be bounded for bounded 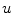 . The multi-dimensional equivalent of the mathematical argument given in [26] starts by integrating Eq. (2.21) over a small volume
. The multi-dimensional equivalent of the mathematical argument given in [26] starts by integrating Eq. (2.21) over a small volume 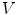 across the boundary
across the boundary 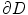 , which yields
, which yields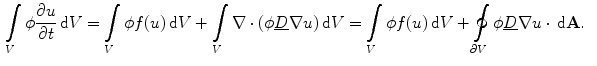
(2.22)

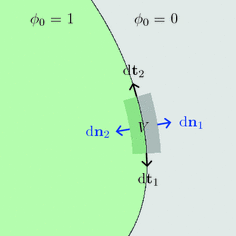
Fig. 2.3
Volume integration at the phase-field interface. Sketch of the integration volume for Eq. (2.22) parallel to the boundary  which is defined by the border between
which is defined by the border between  (green) and
(green) and  (gray). Arrows indicate normal vectors on the surfaces of the integration volume corresponding to the individual terms in Eq. (2.23)
(gray). Arrows indicate normal vectors on the surfaces of the integration volume corresponding to the individual terms in Eq. (2.23)
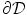 which is defined by the border between
which is defined by the border between 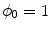 (green) and
(green) and 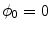 (gray). Arrows indicate normal vectors on the surfaces of the integration volume corresponding to the individual terms in Eq. (2.23)
(gray). Arrows indicate normal vectors on the surfaces of the integration volume corresponding to the individual terms in Eq. (2.23) The geometrical situation is illustrated in Fig. 2.3, with the volume 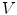 shaded gray. A similar strategy for a different integration path is given in Ref. [28], but the following argumentation applies universally. Denoting the individual contributions to the surface integral separately leads to
shaded gray. A similar strategy for a different integration path is given in Ref. [28], but the following argumentation applies universally. Denoting the individual contributions to the surface integral separately leads to
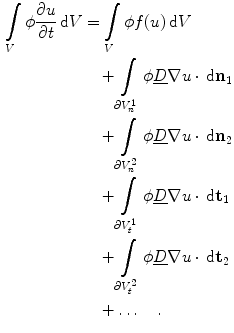
The dots indicate that, in the case of three dimensions, there are two more terms for another direction parallel to the boundary  . However, for everything presented in the following, these terms can be treated analogously to the two explicitly mentioned in Eq. (2.23). For a given interface width
. However, for everything presented in the following, these terms can be treated analogously to the two explicitly mentioned in Eq. (2.23). For a given interface width  of
of  , the normal width of the volume
, the normal width of the volume 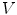 is chosen such that the two boundaries of
is chosen such that the two boundaries of 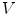 parallel to the boundary
parallel to the boundary 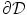 are at iso-
are at iso-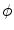 levels of
levels of 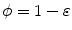 and
and 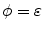 for an arbitrarily small
for an arbitrarily small ![$$\varepsilon >0$$” src=”/wp-content/uploads/2016/11/A328193_1_En_2_Chapter_IEq177.gif”></SPAN>.</DIV><br />
<DIV id=Par24 class=Para>By assuming smooth and bounded solutions <SPAN id=IEq178 class=InlineEquation><IMG alt=$$u$$ src=]() and choosing sufficiently small
and choosing sufficiently small 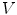 (corresponding to small enough
(corresponding to small enough 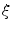 for fixed
for fixed 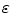 ), the individual integrands of Eq. (2.23) can be approximated by constants, except for the variation due to the factor
), the individual integrands of Eq. (2.23) can be approximated by constants, except for the variation due to the factor 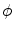 . By then letting
. By then letting 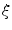 tend to zero, i.e. reducing the width of
tend to zero, i.e. reducing the width of 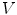 normal to the boundary
normal to the boundary 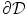 and making
and making 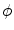 steeper and steeper, the integral on the left hand side and the integrals of the tangential components
steeper and steeper, the integral on the left hand side and the integrals of the tangential components 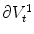 and
and 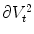 on the right hand side of Eq. (2.23) vanish, because they are integrated over a volume and a surface, respectively, whose size tends to zero. The same is true for the reaction term, which is assumed to be bounded for bounded
on the right hand side of Eq. (2.23) vanish, because they are integrated over a volume and a surface, respectively, whose size tends to zero. The same is true for the reaction term, which is assumed to be bounded for bounded 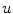 . Using the fact that
. Using the fact that 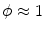 on
on 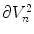 and
and 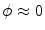 on
on 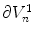 , only one of the two remaining integrals actually has a non-zero contribution, resulting in
, only one of the two remaining integrals actually has a non-zero contribution, resulting in
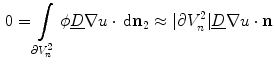
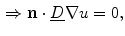
where 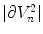 denotes the surface area of
denotes the surface area of 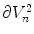 .
.
 shaded gray. A similar strategy for a different integration path is given in Ref. [28], but the following argumentation applies universally. Denoting the individual contributions to the surface integral separately leads to
shaded gray. A similar strategy for a different integration path is given in Ref. [28], but the following argumentation applies universally. Denoting the individual contributions to the surface integral separately leads to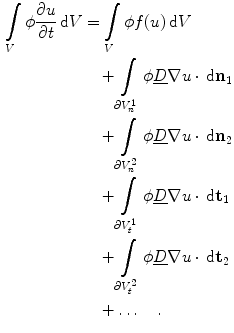
(2.23)
 . However, for everything presented in the following, these terms can be treated analogously to the two explicitly mentioned in Eq. (2.23). For a given interface width
. However, for everything presented in the following, these terms can be treated analogously to the two explicitly mentioned in Eq. (2.23). For a given interface width 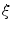 of
of 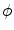 , the normal width of the volume
, the normal width of the volume 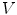 is chosen such that the two boundaries of
is chosen such that the two boundaries of 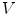 parallel to the boundary
parallel to the boundary 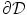 are at iso-
are at iso-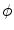 levels of
levels of 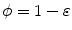 and
and 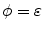 for an arbitrarily small
for an arbitrarily small 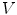 (corresponding to small enough
(corresponding to small enough 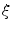 for fixed
for fixed 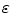 ), the individual integrands of Eq. (2.23) can be approximated by constants, except for the variation due to the factor
), the individual integrands of Eq. (2.23) can be approximated by constants, except for the variation due to the factor 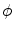 . By then letting
. By then letting 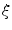 tend to zero, i.e. reducing the width of
tend to zero, i.e. reducing the width of 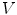 normal to the boundary
normal to the boundary 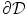 and making
and making 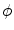 steeper and steeper, the integral on the left hand side and the integrals of the tangential components
steeper and steeper, the integral on the left hand side and the integrals of the tangential components 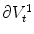 and
and 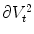 on the right hand side of Eq. (2.23) vanish, because they are integrated over a volume and a surface, respectively, whose size tends to zero. The same is true for the reaction term, which is assumed to be bounded for bounded
on the right hand side of Eq. (2.23) vanish, because they are integrated over a volume and a surface, respectively, whose size tends to zero. The same is true for the reaction term, which is assumed to be bounded for bounded 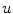 . Using the fact that
. Using the fact that 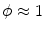 on
on 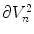 and
and 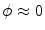 on
on 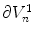 , only one of the two remaining integrals actually has a non-zero contribution, resulting in
, only one of the two remaining integrals actually has a non-zero contribution, resulting in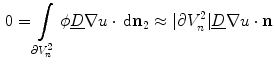
(2.24)
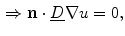
(2.25)
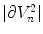 denotes the surface area of
denotes the surface area of 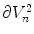 .
.If the above reasoning was justified, Eq. (2.25) would indicate that no-flux boundary conditions are actually implemented by the phase field method. However, it is not known a priori, whether the integrands are bounded independent of the choice of 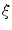 . As the integrands contain derivatives of
. As the integrands contain derivatives of 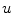 , it is not even sufficient to assume that
, it is not even sufficient to assume that 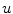 is bounded. Indeed, it is quite natural to expect that by letting
is bounded. Indeed, it is quite natural to expect that by letting 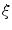 tend to zero and thus approaching the limit of a non-differentiable
tend to zero and thus approaching the limit of a non-differentiable 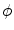 , the gradients of the solution
, the gradients of the solution 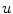 could blow up. Thus, if the crucial assumption of boundedness is not fulfilled, it can neither be concluded that integrals tend to zero because the integrated volume does, nor that for
could blow up. Thus, if the crucial assumption of boundedness is not fulfilled, it can neither be concluded that integrals tend to zero because the integrated volume does, nor that for 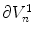 the approximation
the approximation 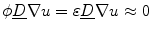 holds (for sufficiently small
holds (for sufficiently small 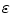 ). In fact, it becomes obvious that the line of thoughts above is not sufficient, if one notes that it would also work without the factor
). In fact, it becomes obvious that the line of thoughts above is not sufficient, if one notes that it would also work without the factor 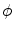 in the volume integrals of Eq. (2.23), which corresponds to the additional prefactor
in the volume integrals of Eq. (2.23), which corresponds to the additional prefactor 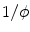 in Eq. (2.19). As will be shown below, this prefactor is vital for the method to yield the desired result.
in Eq. (2.19). As will be shown below, this prefactor is vital for the method to yield the desired result.
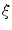 . As the integrands contain derivatives of
. As the integrands contain derivatives of 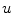 , it is not even sufficient to assume that
, it is not even sufficient to assume that 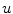 is bounded. Indeed, it is quite natural to expect that by letting
is bounded. Indeed, it is quite natural to expect that by letting 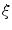 tend to zero and thus approaching the limit of a non-differentiable
tend to zero and thus approaching the limit of a non-differentiable 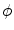 , the gradients of the solution
, the gradients of the solution 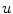 could blow up. Thus, if the crucial assumption of boundedness is not fulfilled, it can neither be concluded that integrals tend to zero because the integrated volume does, nor that for
could blow up. Thus, if the crucial assumption of boundedness is not fulfilled, it can neither be concluded that integrals tend to zero because the integrated volume does, nor that for 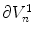 the approximation
the approximation 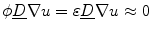 holds (for sufficiently small
holds (for sufficiently small 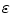 ). In fact, it becomes obvious that the line of thoughts above is not sufficient, if one notes that it would also work without the factor
). In fact, it becomes obvious that the line of thoughts above is not sufficient, if one notes that it would also work without the factor 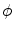 in the volume integrals of Eq. (2.23), which corresponds to the additional prefactor
in the volume integrals of Eq. (2.23), which corresponds to the additional prefactor 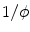 in Eq. (2.19). As will be shown below, this prefactor is vital for the method to yield the desired result.
in Eq. (2.19). As will be shown below, this prefactor is vital for the method to yield the desired result.In a more recent publication [29], Li et al. showed that phase-field methods can be used to model a number of different boundary conditions, no-flux being a special case which can indeed implemented by Eq. (2.21). However, the mechanisms described below by which the phase-field method achieves its goal also explain some important details of the numerical implementation not provided by the very abstract proof in Ref. [29].
2.1.5.3 Mechanism of Boundary Condition Enforcement
Rewriting Eq. (2.21), the terms of the original PDE and the influence of the phase field can be separated:
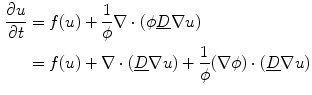
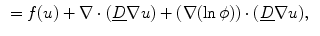
where “ ” in the last two equations is the dot product between two vectors. In Eq. (2.27), the third term only becomes active, if there are components of the current density
” in the last two equations is the dot product between two vectors. In Eq. (2.27), the third term only becomes active, if there are components of the current density 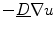 perpendicular to the boundary (i.e. violating the intended no-flux boundary condition), as
perpendicular to the boundary (i.e. violating the intended no-flux boundary condition), as 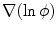 , by definition of the phase field, is just a scaled normal vector:
, by definition of the phase field, is just a scaled normal vector:
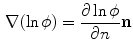
With this information, Eq. (2.27) reads:
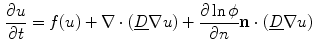
Note that the third term resembles an advection term in fluid dynamics, though the velocity field is not divergence free. Shifting 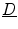 to the other side of the scalar product, the velocity field for the quantity
to the other side of the scalar product, the velocity field for the quantity 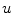 is given by
is given by
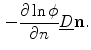
As 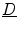 is positive definite,
is positive definite, 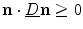 . Taking
. Taking 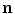 to point out of the domain
to point out of the domain 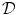 , according to Fig. 2.2c
, according to Fig. 2.2c 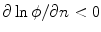 holds, which means that the velocity (2.30) points into the same half-space as
holds, which means that the velocity (2.30) points into the same half-space as 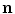 , although it might not be normal to
, although it might not be normal to 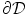 . Therefore,
. Therefore, 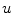 is “advected” outwards with a velocity proportional to
is “advected” outwards with a velocity proportional to 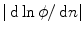 .
.
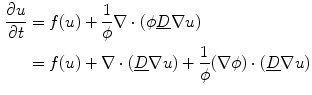
(2.26)
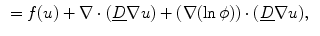
(2.27)
 ” in the last two equations is the dot product between two vectors. In Eq. (2.27), the third term only becomes active, if there are components of the current density
” in the last two equations is the dot product between two vectors. In Eq. (2.27), the third term only becomes active, if there are components of the current density  perpendicular to the boundary (i.e. violating the intended no-flux boundary condition), as
perpendicular to the boundary (i.e. violating the intended no-flux boundary condition), as 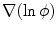 , by definition of the phase field, is just a scaled normal vector:
, by definition of the phase field, is just a scaled normal vector: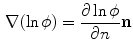
(2.28)
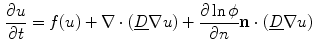
(2.29)
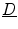 to the other side of the scalar product, the velocity field for the quantity
to the other side of the scalar product, the velocity field for the quantity 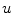 is given by
is given by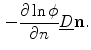
(2.30)
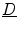 is positive definite,
is positive definite, 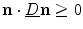 . Taking
. Taking 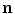 to point out of the domain
to point out of the domain 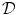 , according to Fig. 2.2c
, according to Fig. 2.2c  holds, which means that the velocity (2.30) points into the same half-space as
holds, which means that the velocity (2.30) points into the same half-space as 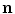 , although it might not be normal to
, although it might not be normal to 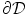 . Therefore,
. Therefore, 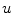 is “advected” outwards with a velocity proportional to
is “advected” outwards with a velocity proportional to 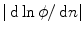 .
.To show that the assumed boundedness of the integrands in Eq. (2.23) is actually present, the so-called maximum principle will be used: If the local reaction term in Eq. (2.21) is ignored for the moment, a pure diffusion equation is obtained. The maximum principle states that the solution 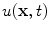 for
for 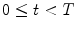 and
and 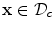 is attained either on the spatial boundary
is attained either on the spatial boundary 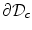 or at some point
or at some point 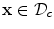 at
at 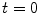 [30]. Another way to say this is: The solution will never exceed the maximum of the initial field
[30]. Another way to say this is: The solution will never exceed the maximum of the initial field 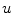 at
at 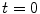 , provided that the values on the boundary
, provided that the values on the boundary 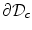 stay below the maximum as well. The same applies to the minimum. For the purpose of the following reasoning, it is assumed that the boundary
stay below the maximum as well. The same applies to the minimum. For the purpose of the following reasoning, it is assumed that the boundary 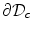 of the auxiliary domain is subject to a passive boundary condition which never attains a maximum or minimum, for example a Dirichlet condition
of the auxiliary domain is subject to a passive boundary condition which never attains a maximum or minimum, for example a Dirichlet condition 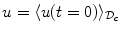 on
on  . Below, it will be argued why the boundary condition on the auxiliary domain is not important for the solution
. Below, it will be argued why the boundary condition on the auxiliary domain is not important for the solution  in the physical domain
in the physical domain  .
.
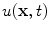 for
for  and
and  is attained either on the spatial boundary
is attained either on the spatial boundary 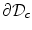 or at some point
or at some point 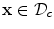 at
at 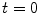 [30]. Another way to say this is: The solution will never exceed the maximum of the initial field
[30]. Another way to say this is: The solution will never exceed the maximum of the initial field 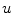 at
at 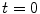 , provided that the values on the boundary
, provided that the values on the boundary 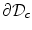 stay below the maximum as well. The same applies to the minimum. For the purpose of the following reasoning, it is assumed that the boundary
stay below the maximum as well. The same applies to the minimum. For the purpose of the following reasoning, it is assumed that the boundary 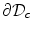 of the auxiliary domain is subject to a passive boundary condition which never attains a maximum or minimum, for example a Dirichlet condition
of the auxiliary domain is subject to a passive boundary condition which never attains a maximum or minimum, for example a Dirichlet condition 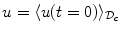 on
on 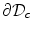 . Below, it will be argued why the boundary condition on the auxiliary domain is not important for the solution
. Below, it will be argued why the boundary condition on the auxiliary domain is not important for the solution 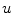 in the physical domain
in the physical domain 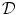 .
.Having the maximum principle at hand, an upper bound for the left hand side of Eq. (2.23) can be obtained by differentiating Eq. (2.21) (still without the local reaction term) with respect to 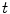 and noting that the time derivative
and noting that the time derivative 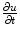 itself therefore fulfills the diffusion equation
itself therefore fulfills the diffusion equation
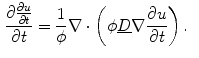
The initial condition 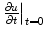 is connected to the initial condition
is connected to the initial condition 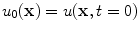 of the original diffusion equation via Eq. (2.21) or (2.29). Given that
of the original diffusion equation via Eq. (2.21) or (2.29). Given that 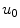 fulfills the no-flux boundary condition in the interface region, the
fulfills the no-flux boundary condition in the interface region, the 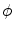 -dependent terms in Eq. (2.29) drop out and thus
-dependent terms in Eq. (2.29) drop out and thus 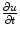 is bounded independent of
is bounded independent of 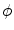 by the maximum principle for all
by the maximum principle for all 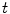 :
:
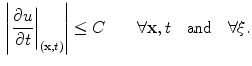
In the context of excitable media, with the source term 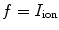 introducing additional
introducing additional 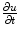 contributions, usually, the fastest time scale of
contributions, usually, the fastest time scale of 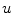 is given by the rise velocity upon activation. The maximum principle therefore ensures that
is given by the rise velocity upon activation. The maximum principle therefore ensures that 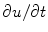 is not increased further by the
is not increased further by the 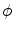 -dependent diffusion dynamics and
-dependent diffusion dynamics and 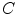 can be interpreted as the upstroke velocity of the action potential.
can be interpreted as the upstroke velocity of the action potential.
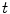 and noting that the time derivative
and noting that the time derivative 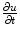 itself therefore fulfills the diffusion equation
itself therefore fulfills the diffusion equation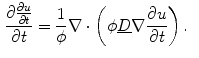
(2.31)
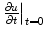 is connected to the initial condition
is connected to the initial condition 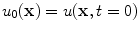 of the original diffusion equation via Eq. (2.21) or (2.29). Given that
of the original diffusion equation via Eq. (2.21) or (2.29). Given that 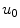 fulfills the no-flux boundary condition in the interface region, the
fulfills the no-flux boundary condition in the interface region, the  -dependent terms in Eq. (2.29) drop out and thus
-dependent terms in Eq. (2.29) drop out and thus 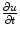 is bounded independent of
is bounded independent of 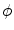 by the maximum principle for all
by the maximum principle for all 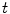 :
: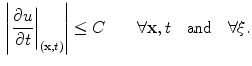
(2.32)
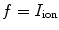 introducing additional
introducing additional 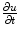 contributions, usually, the fastest time scale of
contributions, usually, the fastest time scale of 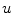 is given by the rise velocity upon activation. The maximum principle therefore ensures that
is given by the rise velocity upon activation. The maximum principle therefore ensures that 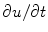 is not increased further by the
is not increased further by the 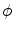 -dependent diffusion dynamics and
-dependent diffusion dynamics and 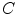 can be interpreted as the upstroke velocity of the action potential.
can be interpreted as the upstroke velocity of the action potential.The boundedness of the integrand involving the reaction term 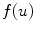 in Eq. (2.23) is seen immediately, because
in Eq. (2.23) is seen immediately, because 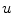 itself is subject to a diffusion equation and thus obeying the maximum principle, if
itself is subject to a diffusion equation and thus obeying the maximum principle, if 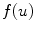 is omitted in Eq. (2.21). Again, this means that the
is omitted in Eq. (2.21). Again, this means that the 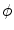 -dependent diffusion dynamics cannot increase or decrease
-dependent diffusion dynamics cannot increase or decrease 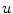 further than determined by the reaction dynamics. Therefore
further than determined by the reaction dynamics. Therefore 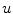 is bounded and so is
is bounded and so is 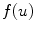 .
.
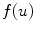 in Eq. (2.23) is seen immediately, because
in Eq. (2.23) is seen immediately, because 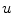 itself is subject to a diffusion equation and thus obeying the maximum principle, if
itself is subject to a diffusion equation and thus obeying the maximum principle, if 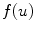 is omitted in Eq. (2.21). Again, this means that the
is omitted in Eq. (2.21). Again, this means that the 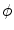 -dependent diffusion dynamics cannot increase or decrease
-dependent diffusion dynamics cannot increase or decrease 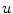 further than determined by the reaction dynamics. Therefore
further than determined by the reaction dynamics. Therefore 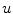 is bounded and so is
is bounded and so is 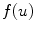 .
.For the remaining terms on the right-hand side of Eq. (2.23), a simpler special case is considered, namely that of a diffusion tensor 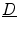 which is nearly spatially constant in the interface region and of an approximately straight boundary, such that spatial derivatives of
which is nearly spatially constant in the interface region and of an approximately straight boundary, such that spatial derivatives of 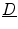 and
and 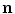 can be neglected.4 Under these assumptions, differentiating Eq. (2.29) in the normal direction yields:
can be neglected.4 Under these assumptions, differentiating Eq. (2.29) in the normal direction yields:
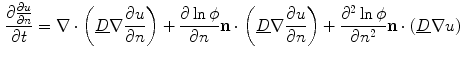
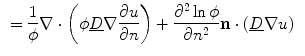
If only the first term on the right hand side was present, 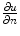 would be bounded by the maximum principle. Due to the shape of the phase field (compare Fig. 2.2 and the beginning of this section),
would be bounded by the maximum principle. Due to the shape of the phase field (compare Fig. 2.2 and the beginning of this section), 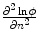 is negative everywhere in the interface region and approaching zero from below in the outward direction. Therefore, the second term on the right hand side is only present in the interface region and opposite in sign to the normal component of the flux
is negative everywhere in the interface region and approaching zero from below in the outward direction. Therefore, the second term on the right hand side is only present in the interface region and opposite in sign to the normal component of the flux 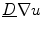 . As
. As 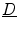 is positive definite, the induced change of
is positive definite, the induced change of 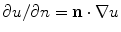 leads to a reduction of the normal component of
leads to a reduction of the normal component of 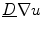 , because in general, for a vector
, because in general, for a vector  with a normal component
with a normal component 
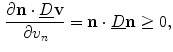
which means that the change of the normal component of 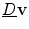 is positive, if the normal component of
is positive, if the normal component of  is increased. The second term in Eq. (2.34) can therefore be viewed as a feedback term that aims at reducing
is increased. The second term in Eq. (2.34) can therefore be viewed as a feedback term that aims at reducing 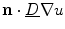 to zero by changing
to zero by changing 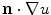 appropriately. This can in principle mean that
appropriately. This can in principle mean that 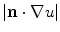 is increased (if
is increased (if 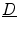 is anisotropic), but zero flux will always be reached at finite values, as indicated above, depending on the parallel components of
is anisotropic), but zero flux will always be reached at finite values, as indicated above, depending on the parallel components of 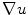 . As the phase field transition length
. As the phase field transition length 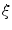 tends to zero, the “feedback strength” is increased. Applying the same strategy for the derivative of
tends to zero, the “feedback strength” is increased. Applying the same strategy for the derivative of 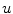 parallel to the boundary yields equations for
parallel to the boundary yields equations for 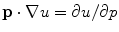 identical to Eq. (2.34), only without the last term. Therefore, this component is bounded by the maximum principle.
identical to Eq. (2.34), only without the last term. Therefore, this component is bounded by the maximum principle.
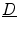 which is nearly spatially constant in the interface region and of an approximately straight boundary, such that spatial derivatives of
which is nearly spatially constant in the interface region and of an approximately straight boundary, such that spatial derivatives of 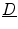 and
and 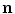 can be neglected.4 Under these assumptions, differentiating Eq. (2.29) in the normal direction yields:
can be neglected.4 Under these assumptions, differentiating Eq. (2.29) in the normal direction yields: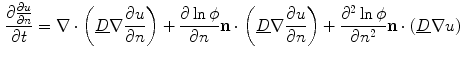
(2.33)
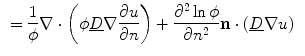
(2.34)
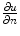 would be bounded by the maximum principle. Due to the shape of the phase field (compare Fig. 2.2 and the beginning of this section),
would be bounded by the maximum principle. Due to the shape of the phase field (compare Fig. 2.2 and the beginning of this section), 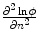 is negative everywhere in the interface region and approaching zero from below in the outward direction. Therefore, the second term on the right hand side is only present in the interface region and opposite in sign to the normal component of the flux
is negative everywhere in the interface region and approaching zero from below in the outward direction. Therefore, the second term on the right hand side is only present in the interface region and opposite in sign to the normal component of the flux 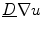 . As
. As 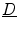 is positive definite, the induced change of
is positive definite, the induced change of 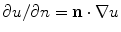 leads to a reduction of the normal component of
leads to a reduction of the normal component of 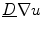 , because in general, for a vector
, because in general, for a vector 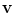 with a normal component
with a normal component 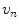
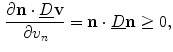
(2.35)
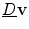 is positive, if the normal component of
is positive, if the normal component of  is increased. The second term in Eq. (2.34) can therefore be viewed as a feedback term that aims at reducing
is increased. The second term in Eq. (2.34) can therefore be viewed as a feedback term that aims at reducing 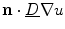 to zero by changing
to zero by changing 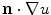 appropriately. This can in principle mean that
appropriately. This can in principle mean that 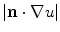 is increased (if
is increased (if 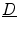 is anisotropic), but zero flux will always be reached at finite values, as indicated above, depending on the parallel components of
is anisotropic), but zero flux will always be reached at finite values, as indicated above, depending on the parallel components of 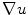 . As the phase field transition length
. As the phase field transition length 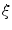 tends to zero, the “feedback strength” is increased. Applying the same strategy for the derivative of
tends to zero, the “feedback strength” is increased. Applying the same strategy for the derivative of 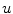 parallel to the boundary yields equations for
parallel to the boundary yields equations for 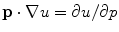 identical to Eq. (2.34), only without the last term. Therefore, this component is bounded by the maximum principle.
identical to Eq. (2.34), only without the last term. Therefore, this component is bounded by the maximum principle.In summary, the gradient 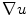 will thus be bounded independent of the steepness of the phase field at the boundary of
will thus be bounded independent of the steepness of the phase field at the boundary of 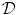 (at least in the approximations used here), which renders the line of thoughts after Eq. (2.23) correct. In addition to verifying the validity of the phase field approach, the above reasoning contains some useful information about the mechanisms, by which the no-flux boundary condition is achieved: Most importantly, one ambiguity of the ansatz (2.19) was removed. It is now clear why simply multiplying
(at least in the approximations used here), which renders the line of thoughts after Eq. (2.23) correct. In addition to verifying the validity of the phase field approach, the above reasoning contains some useful information about the mechanisms, by which the no-flux boundary condition is achieved: Most importantly, one ambiguity of the ansatz (2.19) was removed. It is now clear why simply multiplying 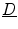 by the phase-field
by the phase-field 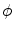 does not lead to the desired results, although Eq. (2.23) apparently suggested this. If this was done, Eq. (2.29) would contain
does not lead to the desired results, although Eq. (2.23) apparently suggested this. If this was done, Eq. (2.29) would contain 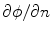 instead of
instead of 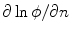 (in addition to a factor
(in addition to a factor  before the diffusion term, which would, however, not have any impact). Replacing
before the diffusion term, which would, however, not have any impact). Replacing  by
by  in Eq. (2.34) would destroy the gradient reduction effect of the second term. Therefore, it would not be possible to conclude that the gradient is bounded.
in Eq. (2.34) would destroy the gradient reduction effect of the second term. Therefore, it would not be possible to conclude that the gradient is bounded.
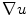 will thus be bounded independent of the steepness of the phase field at the boundary of
will thus be bounded independent of the steepness of the phase field at the boundary of 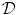 (at least in the approximations used here), which renders the line of thoughts after Eq. (2.23) correct. In addition to verifying the validity of the phase field approach, the above reasoning contains some useful information about the mechanisms, by which the no-flux boundary condition is achieved: Most importantly, one ambiguity of the ansatz (2.19) was removed. It is now clear why simply multiplying
(at least in the approximations used here), which renders the line of thoughts after Eq. (2.23) correct. In addition to verifying the validity of the phase field approach, the above reasoning contains some useful information about the mechanisms, by which the no-flux boundary condition is achieved: Most importantly, one ambiguity of the ansatz (2.19) was removed. It is now clear why simply multiplying 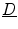 by the phase-field
by the phase-field 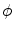 does not lead to the desired results, although Eq. (2.23) apparently suggested this. If this was done, Eq. (2.29) would contain
does not lead to the desired results, although Eq. (2.23) apparently suggested this. If this was done, Eq. (2.29) would contain 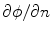 instead of
instead of 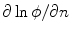 (in addition to a factor
(in addition to a factor 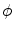 before the diffusion term, which would, however, not have any impact). Replacing
before the diffusion term, which would, however, not have any impact). Replacing 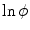 by
by 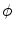 in Eq. (2.34) would destroy the gradient reduction effect of the second term. Therefore, it would not be possible to conclude that the gradient is bounded.
in Eq. (2.34) would destroy the gradient reduction effect of the second term. Therefore, it would not be possible to conclude that the gradient is bounded.Furthermore, when the constant 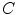 in Eq. (2.32) is interpreted as the upstroke velocity, as suggested, it can be seen from Eq. (2.23) that the accuracy of the method depends on this maximum upstroke velocity. This was also noted in Ref. [26], without, however, taking into account the possibility that this might be caused by the phase field method itself. This has now been ruled out by the line of thoughts above. An additional source of inaccuracy stems from the steepness of gradients arriving at the interface region from inside the domain
in Eq. (2.32) is interpreted as the upstroke velocity, as suggested, it can be seen from Eq. (2.23) that the accuracy of the method depends on this maximum upstroke velocity. This was also noted in Ref. [26], without, however, taking into account the possibility that this might be caused by the phase field method itself. This has now been ruled out by the line of thoughts above. An additional source of inaccuracy stems from the steepness of gradients arriving at the interface region from inside the domain  . Equation (2.34) indicates that the boundary condition of the original problem formulated for
. Equation (2.34) indicates that the boundary condition of the original problem formulated for  has been replaced by a dynamical process that aims at reducing
has been replaced by a dynamical process that aims at reducing 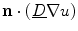 to zero. As this does not happen instantaneously, larger initial gradients mean larger remainders of
to zero. As this does not happen instantaneously, larger initial gradients mean larger remainders of 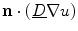 after the reduction process. In excitable media reaction-diffusion systems, the upstroke velocity and the steepness of gradients are, of course, closely related.
after the reduction process. In excitable media reaction-diffusion systems, the upstroke velocity and the steepness of gradients are, of course, closely related.
 in Eq. (2.32) is interpreted as the upstroke velocity, as suggested, it can be seen from Eq. (2.23) that the accuracy of the method depends on this maximum upstroke velocity. This was also noted in Ref. [26], without, however, taking into account the possibility that this might be caused by the phase field method itself. This has now been ruled out by the line of thoughts above. An additional source of inaccuracy stems from the steepness of gradients arriving at the interface region from inside the domain
in Eq. (2.32) is interpreted as the upstroke velocity, as suggested, it can be seen from Eq. (2.23) that the accuracy of the method depends on this maximum upstroke velocity. This was also noted in Ref. [26], without, however, taking into account the possibility that this might be caused by the phase field method itself. This has now been ruled out by the line of thoughts above. An additional source of inaccuracy stems from the steepness of gradients arriving at the interface region from inside the domain  . Equation (2.34) indicates that the boundary condition of the original problem formulated for
. Equation (2.34) indicates that the boundary condition of the original problem formulated for 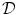 has been replaced by a dynamical process that aims at reducing
has been replaced by a dynamical process that aims at reducing 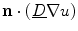 to zero. As this does not happen instantaneously, larger initial gradients mean larger remainders of
to zero. As this does not happen instantaneously, larger initial gradients mean larger remainders of 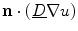 after the reduction process. In excitable media reaction-diffusion systems, the upstroke velocity and the steepness of gradients are, of course, closely related.
after the reduction process. In excitable media reaction-diffusion systems, the upstroke velocity and the steepness of gradients are, of course, closely related.Finally, Eq. (2.29) together with the information illustrated in Fig. 2.2c indicates that the velocity, with which the quantity 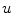 is transported outwards, increases steadily in the interface region and becomes
is transported outwards, increases steadily in the interface region and becomes 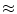
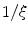 after some distance. The smaller
after some distance. The smaller 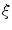 , the less information can therefore travel back from
, the less information can therefore travel back from  to
to 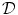 . The only process available for this is the diffusion term in Eq. (2.29), which does not depend on
. The only process available for this is the diffusion term in Eq. (2.29), which does not depend on 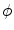 and is therefore arbitrarily slow. This means that the auxiliary (arbitrary) boundary condition applied for numerical reasons at the boundary
and is therefore arbitrarily slow. This means that the auxiliary (arbitrary) boundary condition applied for numerical reasons at the boundary 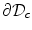 of the auxiliary domain becomes less and less important. This fact is useful for the numerical implementation of the phase field method (see Sect. 2.2.3).
of the auxiliary domain becomes less and less important. This fact is useful for the numerical implementation of the phase field method (see Sect. 2.2.3).
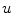 is transported outwards, increases steadily in the interface region and becomes
is transported outwards, increases steadily in the interface region and becomes 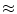
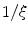 after some distance. The smaller
after some distance. The smaller 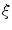 , the less information can therefore travel back from
, the less information can therefore travel back from 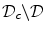 to
to 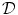 . The only process available for this is the diffusion term in Eq. (2.29), which does not depend on
. The only process available for this is the diffusion term in Eq. (2.29), which does not depend on 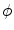 and is therefore arbitrarily slow. This means that the auxiliary (arbitrary) boundary condition applied for numerical reasons at the boundary
and is therefore arbitrarily slow. This means that the auxiliary (arbitrary) boundary condition applied for numerical reasons at the boundary 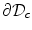 of the auxiliary domain becomes less and less important. This fact is useful for the numerical implementation of the phase field method (see Sect. 2.2.3).
of the auxiliary domain becomes less and less important. This fact is useful for the numerical implementation of the phase field method (see Sect. 2.2.3).2.1.5.4 Extension to Other Boundary Conditions
Although the phase-field method was designed by Fenton et al. to implement no-flux boundary conditions on arbitrary geometries, with the information above, it can be extended to a more general type of Neumann boundary conditions of the type
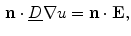
where 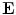 is a fixed vector. This is a special case of Eq. (2.16), when
is a fixed vector. This is a special case of Eq. (2.16), when 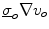 is a constant electric field vector. It is seen immediately from the line of thoughts after Eq. (2.22) that the corresponding phase field replacement in this case is
is a constant electric field vector. It is seen immediately from the line of thoughts after Eq. (2.22) that the corresponding phase field replacement in this case is
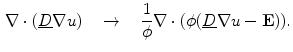
With this substition, Eq. (2.21) is not altered for regions where 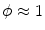 , since
, since 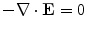 . In the integrals of Eq. (2.23), however, the additional term appears, leading to
. In the integrals of Eq. (2.23), however, the additional term appears, leading to 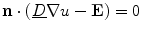 in Eq. (2.25), which is the desired boundary condition. The same result can be obtained from Ref. [29] by starting from Eqs. (2.28) and (2.37) and substituting the correct boundary condition.
in Eq. (2.25), which is the desired boundary condition. The same result can be obtained from Ref. [29] by starting from Eqs. (2.28) and (2.37) and substituting the correct boundary condition.
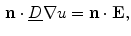
(2.36)
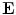 is a fixed vector. This is a special case of Eq. (2.16), when
is a fixed vector. This is a special case of Eq. (2.16), when 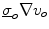 is a constant electric field vector. It is seen immediately from the line of thoughts after Eq. (2.22) that the corresponding phase field replacement in this case is
is a constant electric field vector. It is seen immediately from the line of thoughts after Eq. (2.22) that the corresponding phase field replacement in this case is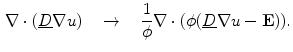
(2.37)
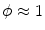 , since
, since 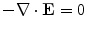 . In the integrals of Eq. (2.23), however, the additional term appears, leading to
. In the integrals of Eq. (2.23), however, the additional term appears, leading to 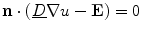 in Eq. (2.25), which is the desired boundary condition. The same result can be obtained from Ref. [29] by starting from Eqs. (2.28) and (2.37) and substituting the correct boundary condition.
in Eq. (2.25), which is the desired boundary condition. The same result can be obtained from Ref. [29] by starting from Eqs. (2.28) and (2.37) and substituting the correct boundary condition.2.1.6 Models
So far, in this chapter, the cross-membrane current 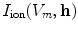 in, e.g., Eqs. (2.4), (2.9) or (2.13) has been treated as an unknown quantity whose dynamics is determined by the membrane potential
in, e.g., Eqs. (2.4), (2.9) or (2.13) has been treated as an unknown quantity whose dynamics is determined by the membrane potential 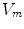 and an additional set of equations for the local (i.e. spatially uncoupled) variables
and an additional set of equations for the local (i.e. spatially uncoupled) variables 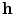 . As described in Sect. 2.1.1, one approach to construct this term is to empirically determine the contributions of all different ion species and membrane compounds that lead to transmembrane currents. Indeed, many models based on this bottom-up approach exist, although they are by definition based on incomplete data. A comprehensive list of physiological models, ordered by tissue type (atrial/ventricular) and species can be found in Ref. [31]. One advantage of this approach is that model parameters can directly be related to physiological properties, which enables investigations of genetic defects and facilitates the adaption of the model for disease conditions. However, a major drawback of these models is their computational cost, due to the large number of local variables used. One extreme example is the Wang-Sobie model for neonatal rat ventricular myocytes [15] with 35 dynamic variables and 74 parameters. Although the large number of parameters might be beneficial for the reasons mentioned above, it is at the same time hindering generic approaches such as parameter scans or fitting procedures. Also, for most physiological models, sensitivity of the dynamics to individual parameters is not documented, which further complicates the analysis.
. As described in Sect. 2.1.1, one approach to construct this term is to empirically determine the contributions of all different ion species and membrane compounds that lead to transmembrane currents. Indeed, many models based on this bottom-up approach exist, although they are by definition based on incomplete data. A comprehensive list of physiological models, ordered by tissue type (atrial/ventricular) and species can be found in Ref. [31]. One advantage of this approach is that model parameters can directly be related to physiological properties, which enables investigations of genetic defects and facilitates the adaption of the model for disease conditions. However, a major drawback of these models is their computational cost, due to the large number of local variables used. One extreme example is the Wang-Sobie model for neonatal rat ventricular myocytes [15] with 35 dynamic variables and 74 parameters. Although the large number of parameters might be beneficial for the reasons mentioned above, it is at the same time hindering generic approaches such as parameter scans or fitting procedures. Also, for most physiological models, sensitivity of the dynamics to individual parameters is not documented, which further complicates the analysis.
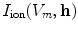 in, e.g., Eqs. (2.4), (2.9) or (2.13) has been treated as an unknown quantity whose dynamics is determined by the membrane potential
in, e.g., Eqs. (2.4), (2.9) or (2.13) has been treated as an unknown quantity whose dynamics is determined by the membrane potential  and an additional set of equations for the local (i.e. spatially uncoupled) variables
and an additional set of equations for the local (i.e. spatially uncoupled) variables  . As described in Sect. 2.1.1, one approach to construct this term is to empirically determine the contributions of all different ion species and membrane compounds that lead to transmembrane currents. Indeed, many models based on this bottom-up approach exist, although they are by definition based on incomplete data. A comprehensive list of physiological models, ordered by tissue type (atrial/ventricular) and species can be found in Ref. [31]. One advantage of this approach is that model parameters can directly be related to physiological properties, which enables investigations of genetic defects and facilitates the adaption of the model for disease conditions. However, a major drawback of these models is their computational cost, due to the large number of local variables used. One extreme example is the Wang-Sobie model for neonatal rat ventricular myocytes [15] with 35 dynamic variables and 74 parameters. Although the large number of parameters might be beneficial for the reasons mentioned above, it is at the same time hindering generic approaches such as parameter scans or fitting procedures. Also, for most physiological models, sensitivity of the dynamics to individual parameters is not documented, which further complicates the analysis.
. As described in Sect. 2.1.1, one approach to construct this term is to empirically determine the contributions of all different ion species and membrane compounds that lead to transmembrane currents. Indeed, many models based on this bottom-up approach exist, although they are by definition based on incomplete data. A comprehensive list of physiological models, ordered by tissue type (atrial/ventricular) and species can be found in Ref. [31]. One advantage of this approach is that model parameters can directly be related to physiological properties, which enables investigations of genetic defects and facilitates the adaption of the model for disease conditions. However, a major drawback of these models is their computational cost, due to the large number of local variables used. One extreme example is the Wang-Sobie model for neonatal rat ventricular myocytes [15] with 35 dynamic variables and 74 parameters. Although the large number of parameters might be beneficial for the reasons mentioned above, it is at the same time hindering generic approaches such as parameter scans or fitting procedures. Also, for most physiological models, sensitivity of the dynamics to individual parameters is not documented, which further complicates the analysis.On the other end of the spectrum, generic models are created using a top-down approach to the model construction problem. Rather than incorporating every possible detail of the system for which information exists, they try to mimic the basic properties of cardiac tissue (or even more generic: of excitable media) using the fewest number of variables and parameters possible to achieve a particular degree of realism. A very generic model for excitable media is the Barkley model [32], which consists of only two variables and three parameters which determine the basic properties of the medium such as the excitability, excitation threshold and duration. The Barkley model will be used in this work for numerical simulations, when values of physiological parameters are not important or unknown and when results are to be obtained for the large class of excitable media. In all other simulations, the somewhat more detailed three-variable Fenton-Karma model [33] will be used, which has 14 parameters that enable it to reproduce important aspects of the dynamics of more realistic cardiac models.
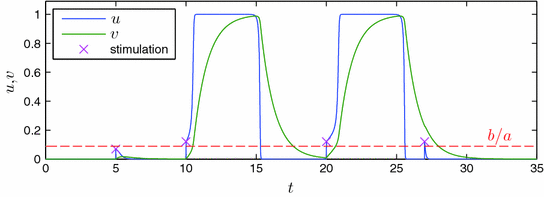

Fig. 2.4
Barkley model dynamics. Four attempts, marked by “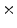 ”, to induce an excitation in the Barkley model (without diffusion) by instantaneously setting the model variable
”, to induce an excitation in the Barkley model (without diffusion) by instantaneously setting the model variable 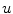 . In the first case, the stimulation is subthreshold. The second and third stimulation produce almost identical excitations, whereas the fourth stimulation occurs at a time when excitability is not fully recovered yet, as
. In the first case, the stimulation is subthreshold. The second and third stimulation produce almost identical excitations, whereas the fourth stimulation occurs at a time when excitability is not fully recovered yet, as  has not returned to zero. Because of this refractoriness, the stimulation fails to produce an excitation. Model parameters: B1 (see Table A.1, p. 184)
has not returned to zero. Because of this refractoriness, the stimulation fails to produce an excitation. Model parameters: B1 (see Table A.1, p. 184)
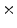 ”, to induce an excitation in the Barkley model (without diffusion) by instantaneously setting the model variable
”, to induce an excitation in the Barkley model (without diffusion) by instantaneously setting the model variable 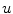 . In the first case, the stimulation is subthreshold. The second and third stimulation produce almost identical excitations, whereas the fourth stimulation occurs at a time when excitability is not fully recovered yet, as
. In the first case, the stimulation is subthreshold. The second and third stimulation produce almost identical excitations, whereas the fourth stimulation occurs at a time when excitability is not fully recovered yet, as 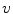 has not returned to zero. Because of this refractoriness, the stimulation fails to produce an excitation. Model parameters: B1 (see Table A.1, p. 184)
has not returned to zero. Because of this refractoriness, the stimulation fails to produce an excitation. Model parameters: B1 (see Table A.1, p. 184) 2.1.6.1 The Barkley and the Bär-Eiswirth Model
This two-variable, generic model was developed by Barkley in the beginning of the 1990s in an effort to understand spiral wave dynamics in generic excitable media. Although already used in Ref. [32], it was newly introduced in its most efficient numerical form in Ref. [34]. Its equations are
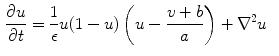
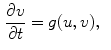
with the parameters 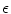 ,
, 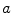 and
and 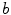 . For the original Barkley model,
. For the original Barkley model, 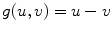 . The fast variable
. The fast variable 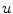 can be identified as a normalized
can be identified as a normalized 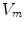 in the mono-domain formalism of Sect. 2.1.3, while the local part on the right hand side of the
in the mono-domain formalism of Sect. 2.1.3, while the local part on the right hand side of the 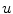 -equation represents the cross-membrane current term
-equation represents the cross-membrane current term 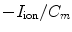 . There is only one local variable, such that
. There is only one local variable, such that 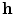 is actually a scalar and
is actually a scalar and 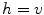 . The diffusion tensor is normalized to
. The diffusion tensor is normalized to 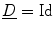 . An example of the local dynamics of the model, i.e. without the diffusion term, following a series of stimulations is shown in Fig. 2.4. It can be understood from the
. An example of the local dynamics of the model, i.e. without the diffusion term, following a series of stimulations is shown in Fig. 2.4. It can be understood from the  phase space structure, which is typical for simple excitable systems5 and is depicted in Fig. 2.5. It has a stable fixed point at
phase space structure, which is typical for simple excitable systems5 and is depicted in Fig. 2.5. It has a stable fixed point at 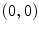 , whose basin of attraction is the whole square
, whose basin of attraction is the whole square ![$$[0,1[\times [0,1]$$](/wp-content/uploads/2016/11/A328193_1_En_2_Chapter_IEq330.gif) , but trajectories starting a considerable distance6 right of the nullcline
, but trajectories starting a considerable distance6 right of the nullcline 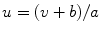 make a large detour close to
make a large detour close to 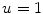 ,
, 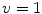 and
and 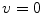 before returning to the fixed point. In contrast, trajectories starting close to
before returning to the fixed point. In contrast, trajectories starting close to 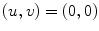 return directly. The first case corresponds to action potential following a superthreshold depolarization, whereas the second is a subthreshold depolarization not strong enough to evoke an action potential. The meaning of the three parameters in terms of the characteristics of excitable media can readily be read off the phase space diagram:
return directly. The first case corresponds to action potential following a superthreshold depolarization, whereas the second is a subthreshold depolarization not strong enough to evoke an action potential. The meaning of the three parameters in terms of the characteristics of excitable media can readily be read off the phase space diagram: 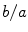 is the excitation threshold during rest, whereas
is the excitation threshold during rest, whereas 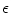 determines the time scale of
determines the time scale of 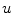 compared to
compared to 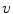 . Its main impact is on the upstroke velocity of an action potential, which also determines the conduction velocity in the spatially extended case in conjunction with diffusion.
. Its main impact is on the upstroke velocity of an action potential, which also determines the conduction velocity in the spatially extended case in conjunction with diffusion. 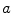 on its own mainly influences the action potential duration, as it determines the slope of the above-mentioned nullcline and thus the value of
on its own mainly influences the action potential duration, as it determines the slope of the above-mentioned nullcline and thus the value of 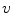 at which
at which 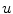 starts to decrease.
starts to decrease.
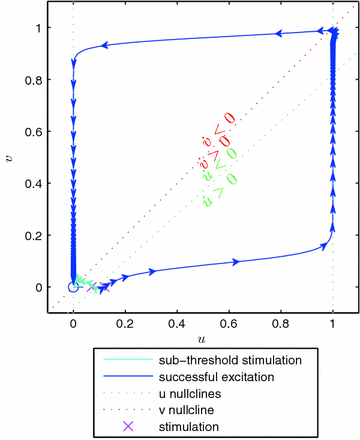
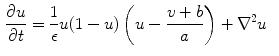
(2.38a)
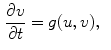
(2.38b)
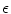 ,
, 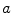 and
and 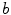 . For the original Barkley model,
. For the original Barkley model, 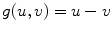 . The fast variable
. The fast variable 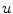 can be identified as a normalized
can be identified as a normalized 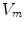 in the mono-domain formalism of Sect. 2.1.3, while the local part on the right hand side of the
in the mono-domain formalism of Sect. 2.1.3, while the local part on the right hand side of the 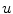 -equation represents the cross-membrane current term
-equation represents the cross-membrane current term 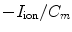 . There is only one local variable, such that
. There is only one local variable, such that 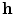 is actually a scalar and
is actually a scalar and 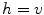 . The diffusion tensor is normalized to
. The diffusion tensor is normalized to 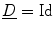 . An example of the local dynamics of the model, i.e. without the diffusion term, following a series of stimulations is shown in Fig. 2.4. It can be understood from the
. An example of the local dynamics of the model, i.e. without the diffusion term, following a series of stimulations is shown in Fig. 2.4. It can be understood from the  phase space structure, which is typical for simple excitable systems5 and is depicted in Fig. 2.5. It has a stable fixed point at
phase space structure, which is typical for simple excitable systems5 and is depicted in Fig. 2.5. It has a stable fixed point at 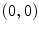 , whose basin of attraction is the whole square
, whose basin of attraction is the whole square ![$$[0,1[\times [0,1]$$](/wp-content/uploads/2016/11/A328193_1_En_2_Chapter_IEq330.gif) , but trajectories starting a considerable distance6 right of the nullcline
, but trajectories starting a considerable distance6 right of the nullcline 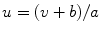 make a large detour close to
make a large detour close to 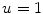 ,
, 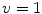 and
and 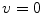 before returning to the fixed point. In contrast, trajectories starting close to
before returning to the fixed point. In contrast, trajectories starting close to 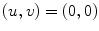 return directly. The first case corresponds to action potential following a superthreshold depolarization, whereas the second is a subthreshold depolarization not strong enough to evoke an action potential. The meaning of the three parameters in terms of the characteristics of excitable media can readily be read off the phase space diagram:
return directly. The first case corresponds to action potential following a superthreshold depolarization, whereas the second is a subthreshold depolarization not strong enough to evoke an action potential. The meaning of the three parameters in terms of the characteristics of excitable media can readily be read off the phase space diagram: 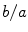 is the excitation threshold during rest, whereas
is the excitation threshold during rest, whereas 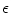 determines the time scale of
determines the time scale of 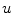 compared to
compared to 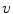 . Its main impact is on the upstroke velocity of an action potential, which also determines the conduction velocity in the spatially extended case in conjunction with diffusion.
. Its main impact is on the upstroke velocity of an action potential, which also determines the conduction velocity in the spatially extended case in conjunction with diffusion. 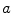 on its own mainly influences the action potential duration, as it determines the slope of the above-mentioned nullcline and thus the value of
on its own mainly influences the action potential duration, as it determines the slope of the above-mentioned nullcline and thus the value of 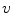 at which
at which 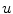 starts to decrease.
starts to decrease.
Fig. 2.5
Barkley model: local phase space. Shown are two stimulation attempts from the fully recovered state: one is subthreshold (cyan), causing the system to return immediately to the stable fixed point at (0,0), whereas the other one is far enough in the ![$$\dot{u}>0$$” src=”/wp-content/uploads/2016/11/A328193_1_En_2_Chapter_IEq347.gif”></SPAN> region to produce an excitation (<SPAN class=EmphasisTypeItalic>blue</SPAN>). <SPAN class=EmphasisTypeItalic>Arrows</SPAN> on the trajectories mark equidistant time points, indicating the fast dynamics of <SPAN id=IEq348 class=InlineEquation><IMG alt=$$u$$ src=]() compared to
compared to 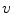 . The tilted
. The tilted 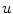 nullcline has the equation
nullcline has the equation 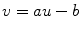 and is responsible for the refractoriness shortly after an excitation, when still
and is responsible for the refractoriness shortly after an excitation, when still 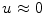 : in this case, the distance to the right necessary to cross the
: in this case, the distance to the right necessary to cross the 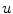 nullcline is considerably increased. When
nullcline is considerably increased. When 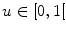 it is
it is 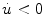 . Model parameters: B1 (see Table A.1, p. 184)
. Model parameters: B1 (see Table A.1, p. 184)
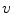 . The tilted
. The tilted 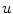 nullcline has the equation
nullcline has the equation 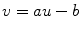 and is responsible for the refractoriness shortly after an excitation, when still
and is responsible for the refractoriness shortly after an excitation, when still 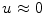 : in this case, the distance to the right necessary to cross the
: in this case, the distance to the right necessary to cross the 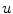 nullcline is considerably increased. When
nullcline is considerably increased. When 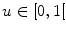 it is
it is 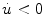 . Model parameters: B1 (see Table A.1, p. 184)
. Model parameters: B1 (see Table A.1, p. 184)Despite its simplicity, the Barkley model (now, again, including the Laplacian term) supports a large number of different wave patterns, including pulses, plane waves and both stationary and meandering spiral waves. However, there are no (homogeneous) parameters for which the Barkley displays spiral wave breakup or other types of chaos. It was shown by Bär and Eiswirth that turbulence can be observed by delaying the increase of the slow variable 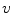 . This can be done by redefining
. This can be done by redefining 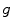 in Eq. (2.38b) as follows [37]:
in Eq. (2.38b) as follows [37]:
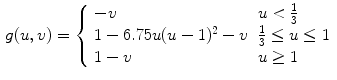
This modification will be referred to as the Bär-Eiswirth model in the rest of this thesis.
 . This can be done by redefining
. This can be done by redefining  in Eq. (2.38b) as follows [37]:
in Eq. (2.38b) as follows [37]: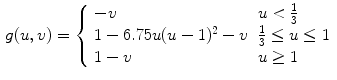
(2.39)
2.1.6.2 The Fenton-Karma Model
The equations for this generic model were developed by Fenton and Karma in 1998 with the aim of capturing the most important features specific to cardiac models (as opposed to general excitable media). Consequently, although the model has only three variables, it is considerably more tightly connected to the physiological mechanisms of excitability in the cardiac muscle. The model considers three cross-membrane currents, named fast inward (fi), slow outward (so) and slow inward (si) current. These roughly correspond to the sodium, potassium and calcium currents, respectively (cf. Sect. 1.2.1). However, the complexity of different ion channel types and other contributions to membrane potential dynamics has been condensed into these net currents and their activation and inactivation. Therefore, the parameters (most of which are timescales and thresholds) have a physiological meaning in that they reflect typical or net properties of these summarized currents, but nevertheless they cannot be interpreted as descriptions of the microscopic components responsible for membrane potential dynamics.
The equations of the Fenton-Karma model are
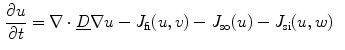
where the three cross-membrane currents are defined as
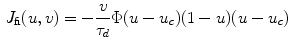
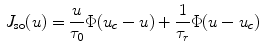
![$$\begin{aligned} J_\text {si}(u,w)&= -\frac{w}{2\tau _{si}}(1+\tanh [k(u-u_c^{si})]). \end{aligned}$$](/wp-content/uploads/2016/11/A328193_1_En_2_Chapter_Equ54.gif)
The sum of these currents corresponds to the term 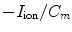 of Sect. 2.1.3. Again,
of Sect. 2.1.3. Again, 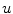 is a normalized membrane potential
is a normalized membrane potential 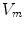 and on the order 0 to 1, such that one unit of
and on the order 0 to 1, such that one unit of 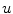 roughly corresponds to a 100 mV membrane potential change. The vector of local variables for the Fenton-Karma model therefore is
roughly corresponds to a 100 mV membrane potential change. The vector of local variables for the Fenton-Karma model therefore is 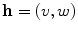 .
.
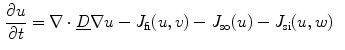
(2.40a)
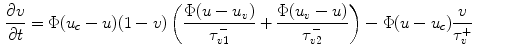
(2.40b)
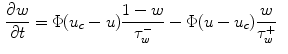
(2.40c)
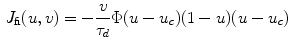
(2.41a)
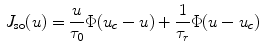
(2.41b)
![$$\begin{aligned} J_\text {si}(u,w)&= -\frac{w}{2\tau _{si}}(1+\tanh [k(u-u_c^{si})]). \end{aligned}$$](/wp-content/uploads/2016/11/A328193_1_En_2_Chapter_Equ54.gif)
(2.41c)
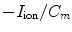 of Sect. 2.1.3. Again,
of Sect. 2.1.3. Again, 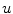 is a normalized membrane potential
is a normalized membrane potential 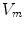 and on the order 0 to 1, such that one unit of
and on the order 0 to 1, such that one unit of 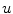 roughly corresponds to a 100 mV membrane potential change. The vector of local variables for the Fenton-Karma model therefore is
roughly corresponds to a 100 mV membrane potential change. The vector of local variables for the Fenton-Karma model therefore is 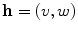 .
.In its original published form, the function 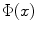 in Eqs. (2.40) and (2.41) is simply the step function
in Eqs. (2.40) and (2.41) is simply the step function
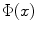 in Eqs. (2.40) and (2.41) is simply the step function
in Eqs. (2.40) and (2.41) is simply the step function