Fig. 6.1
Number of full-length papers by year available on PubMed dealing with deformable registration for radiation therapy. The numbers documented correspond to the hits of a search with terms “deformable registration” and “radiotherapy” (and related terms such as “radiation therapy”, “non-rigid registration”, “non-linear registration”, etc.)
Registration is the task of retrieving the unknown spatial transformation that puts two images in correspondence, by aligning the imaged objects. For deformable image registration, the mapping can be spatially varying, and is usually locally or semi-locally defined. Intensity-based DIR (IB-DIR) consists in considering the pixel intensity values to retrieve that mapping, in contrast to other approaches such as biophysical modeling (see Chap. 4) or surface- and landmark-based registration techniques (see Chap. 5). No preprocessing involving image segmentation or feature extraction is generally required and only the intensity distributions of the images are used.
The difficulty of deformable registration is twofold. First of all, the problem is ill-posed. A problem is said to be well-posed when a solution exists, is unique, and depends continuously on the initial data. A problem is ill-posed when it fails to satisfy at least one of these criteria. As a consequence, it is important to incorporate prior knowledge about the sought transformation in the registration framework, limiting the search space to physically or physiologically plausible solutions. Several approaches have been proposed to do so, and we will present some general mechanisms in the following sections. Methods specifically developed for images of the thorax are discussed in Chap. 7.
A second issue of DIR is that there is no standardized means for evaluating the accuracy of the result. On real patient images, establishing a reference is a tedious and time-consuming task, and the validation obtained is partial and only locally valid due to the large amount of degrees of freedom. Despite numerous recent efforts, evaluation of DIR remains challenging. Validation of DIR will be extensively discussed in Chap. 8.
6.1.2 General Framework
Registration is commonly formulated as an optimization problem which aims at finding the spatial transformation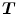 , that minimizes a cost function over a fixed image
, that minimizes a cost function over a fixed image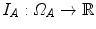 and a moving image
and a moving image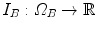 with
with 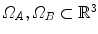 , given the coordinate transformation
, given the coordinate transformation 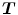 (see Eq. (6.1)).
(see Eq. (6.1)).
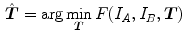
Equation (6.1) can usually not be solved directly, but an estimate of the optimal transformation is obtained through an iterative optimization process.
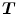 , that minimizes a cost function over a fixed image
, that minimizes a cost function over a fixed image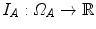 and a moving image
and a moving image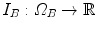 with
with 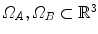 , given the coordinate transformation
, given the coordinate transformation 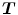 (see Eq. (6.1)).
(see Eq. (6.1)).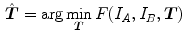
(6.1)
A general framework of the registration procedure is presented in Fig. 6.2. Assume the procedure is started with an initial transformation. The latter can be applied to the moving image, effectively mapping it to the coordinate space of the fixed image. The result of the cost function can be computed, expressing the fitness of the current mapping. The optimizer can then propose a new set of transformation parameters based on this measure in an attempt to improve the matching, and the iteration loop is repeated until convergence.
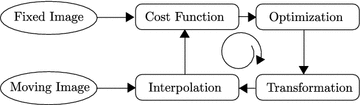

Fig. 6.2
A general registration framework indicating the main components of the iterative registration procedure. Following Ibanez et al. [25]
It is important to note that registration takes place in physical space. As images are generally available as discrete representations, computing the fitness value between a fixed image and a transformed moving image will require evaluating the moving image at non-grid positions using interpolation. Commonly used interpolation schemes include nearest neighbor interpolation, linear interpolation and B-spline interpolation [33]. Interpolation will not be discussed further. The remaining registration components will be described in detail in the following sections.
6.1.3 Transformation
The term transformation is used here to refer to the mathematical expression of the spatial mapping between the coordinate spaces of the images. It is defined by the parametrization used to represent the deformation and subsequently determines the search space over which the optimization is to be performed. The transformation is one of the components that allows to enforce a transformation model, in which deformations are favored that respect certain mathematical or physical laws, or mimic some particular physiological behavior (see Holden et al. [24] for an excellent review on transformation models).
By convention, the transformation is defined as mapping points from the coordinate space of the fixed image to coordinate space of the moving image, i.e. the position 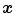 in the image
in the image 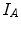 is mapped to a corresponding position
is mapped to a corresponding position 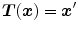 in image
in image 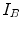 . Observe that by retrieving the intensities of the moving image at the transformed grid positions of the fixed image—using interpolation, one effectively warps the moving image to the coordinate space of fixed image.
. Observe that by retrieving the intensities of the moving image at the transformed grid positions of the fixed image—using interpolation, one effectively warps the moving image to the coordinate space of fixed image.
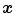 in the image
in the image 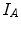 is mapped to a corresponding position
is mapped to a corresponding position 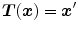 in image
in image 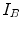 . Observe that by retrieving the intensities of the moving image at the transformed grid positions of the fixed image—using interpolation, one effectively warps the moving image to the coordinate space of fixed image.
. Observe that by retrieving the intensities of the moving image at the transformed grid positions of the fixed image—using interpolation, one effectively warps the moving image to the coordinate space of fixed image.Based on the support of the underlying functions, roughly three groups of parametrizations can be distinguished to represent a deformable transformation: global, semi-local and local. Global representations include transformations expressed using harmonic functions or global polynomials, such as thin plate splines or radial basis functions. Semi-local transformations are expressed using functions with a compact support, such as wavelets and B-splines. They tend to be more suited for representing highly localized deformation, in addition to being advantageous during optimization because of their reduced complexity. Local parametrizations are typically dense vector fields, in which a vector is used for representing the displacement of a single voxel.
6.1.4 Similarity Measure
The cost function 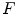 should quantify the fitness of a transformation between two images. The cost function usually represents a compromise between image similarity and deformation regularity, e.g.
should quantify the fitness of a transformation between two images. The cost function usually represents a compromise between image similarity and deformation regularity, e.g.
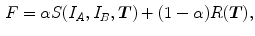
in which 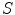 is a dissimilarity metric which evaluates the correspondence between the image intensity distributions in a predefined metric space, given the transformation.
is a dissimilarity metric which evaluates the correspondence between the image intensity distributions in a predefined metric space, given the transformation. 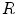 is a regularization term favoring certain properties in the transformation and will be discussed in Sect. 6.1.5.
is a regularization term favoring certain properties in the transformation and will be discussed in Sect. 6.1.5.
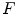 should quantify the fitness of a transformation between two images. The cost function usually represents a compromise between image similarity and deformation regularity, e.g.
should quantify the fitness of a transformation between two images. The cost function usually represents a compromise between image similarity and deformation regularity, e.g.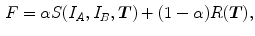
(6.2)
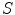 is a dissimilarity metric which evaluates the correspondence between the image intensity distributions in a predefined metric space, given the transformation.
is a dissimilarity metric which evaluates the correspondence between the image intensity distributions in a predefined metric space, given the transformation. 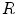 is a regularization term favoring certain properties in the transformation and will be discussed in Sect. 6.1.5.
is a regularization term favoring certain properties in the transformation and will be discussed in Sect. 6.1.5.Based on the nature of the dissimilarity metric 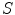 , we can make a distinction between feature-based and intensity-based approaches, or hybrid approaches that are a combination of both. Feature-based approaches rely on the matching of landmarks, segmentations or other features extracted from the images prior to registration, and are the subject of Chap. 5.
, we can make a distinction between feature-based and intensity-based approaches, or hybrid approaches that are a combination of both. Feature-based approaches rely on the matching of landmarks, segmentations or other features extracted from the images prior to registration, and are the subject of Chap. 5.
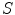 , we can make a distinction between feature-based and intensity-based approaches, or hybrid approaches that are a combination of both. Feature-based approaches rely on the matching of landmarks, segmentations or other features extracted from the images prior to registration, and are the subject of Chap. 5.
, we can make a distinction between feature-based and intensity-based approaches, or hybrid approaches that are a combination of both. Feature-based approaches rely on the matching of landmarks, segmentations or other features extracted from the images prior to registration, and are the subject of Chap. 5.6.1.4.1 Theoretical Background of Intensity-Based Similarity Measures
Intensity-based similarity between two images is quantified by measuring a link between the intensity distributions of the image pair. The underlying assumption is that this link will become stronger when images are well registered, and inversely will become weaker as the quality of the registration decreases. The link should exist because images are acquired from the same physical structure using two different devices or at two different times, or from the corresponding structure belonging to different subjects.
The link is evaluated through the concept of dependency. The intensity distributions are said to be dependent when a variation in one distribution leads to variation in the other. Note that dependence does not mean causality. The term correlation is generally used when the relationship is reciprocal. If there is no link, intensity distributions are independent, whereas if the knowledge of one distribution allows to perfectly predict the second, the link is said to be functional; i.e. there exists a function 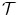 allowing to map a grey-level from one distribution to a grey-level of the other; i.e.
allowing to map a grey-level from one distribution to a grey-level of the other; i.e. 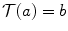 . Again, note that this relationship is not necessarily reciprocal.
. Again, note that this relationship is not necessarily reciprocal.
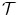 allowing to map a grey-level from one distribution to a grey-level of the other; i.e.
allowing to map a grey-level from one distribution to a grey-level of the other; i.e. 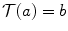 . Again, note that this relationship is not necessarily reciprocal.
. Again, note that this relationship is not necessarily reciprocal.The concept of variation plays an important role in the evaluation of the dependency. Dependency is often regarded as the reduction of the variation of a distribution caused by the knowledge of the other. Different definitions of the type of variation lead to different measures. We can therefore define the term intensity-based similarity measure in the following way: it is a function that measures a type of dependency between the distributions of the intensities that characterize the images.
6.1.4.2 Joint Histogram
The majority of the existing intensity-based similarity measures can be computed (even though it is not always necessary) from the same mathematical object called the joint histogram. It is essentially a 2D matrix 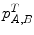 , that summarizes the statistical link between the intensity distributions of the images for a given transformation.
, that summarizes the statistical link between the intensity distributions of the images for a given transformation. 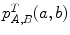 represents the probability of having the intensity
represents the probability of having the intensity 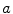 in the image
in the image 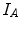 and
and 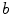 in image
in image 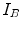 at the same spatial location, for a given transformation
at the same spatial location, for a given transformation 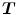 .
.
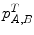 , that summarizes the statistical link between the intensity distributions of the images for a given transformation.
, that summarizes the statistical link between the intensity distributions of the images for a given transformation. 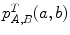 represents the probability of having the intensity
represents the probability of having the intensity 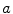 in the image
in the image 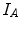 and
and 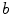 in image
in image 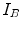 at the same spatial location, for a given transformation
at the same spatial location, for a given transformation 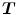 .
.In practice, it is computed by looping over all pixel positions 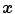 in the image
in the image 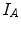 and looking at the corresponding
and looking at the corresponding 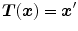 position in image
position in image 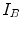 . As we are dealing with discrete images, interpolation is required and several methods can be used to deal with non-integer pixel positions. Conventional approaches involve nearest neighbor interpolation, linear interpolation and partial volume [37].
. As we are dealing with discrete images, interpolation is required and several methods can be used to deal with non-integer pixel positions. Conventional approaches involve nearest neighbor interpolation, linear interpolation and partial volume [37].
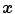 in the image
in the image 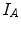 and looking at the corresponding
and looking at the corresponding 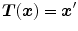 position in image
position in image 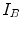 . As we are dealing with discrete images, interpolation is required and several methods can be used to deal with non-integer pixel positions. Conventional approaches involve nearest neighbor interpolation, linear interpolation and partial volume [37].
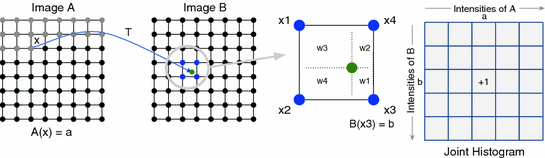
. As we are dealing with discrete images, interpolation is required and several methods can be used to deal with non-integer pixel positions. Conventional approaches involve nearest neighbor interpolation, linear interpolation and partial volume [37].The process is illustrated for two dimensional images in Fig. 6.3. Suppose 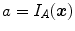 and
and 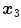 is the nearest pixel position of
is the nearest pixel position of 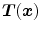 in
in 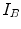 with
with 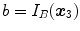 the intensity in
the intensity in 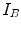 . For nearest neighbor interpolation, the joint intensity matrix
. For nearest neighbor interpolation, the joint intensity matrix 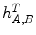 is updated by
is updated by 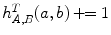 . Using a linear interpolation approach, the intensity is first interpolated,
. Using a linear interpolation approach, the intensity is first interpolated, 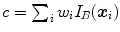 , and used to update the histogram
, and used to update the histogram 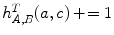 . Using the partial volume approach, the histogram is updated for four intensities
. Using the partial volume approach, the histogram is updated for four intensities 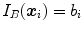 , with
, with 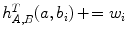 , which tends to give smoother histograms. The computed frequencies of joint intensities are normalized to the number of overlapping voxels
, which tends to give smoother histograms. The computed frequencies of joint intensities are normalized to the number of overlapping voxels 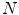 , resulting in the joint probabilities
, resulting in the joint probabilities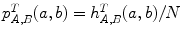 .
.
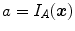 and
and 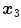 is the nearest pixel position of
is the nearest pixel position of 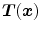 in
in 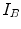 with
with 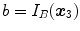 the intensity in
the intensity in 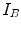 . For nearest neighbor interpolation, the joint intensity matrix
. For nearest neighbor interpolation, the joint intensity matrix 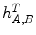 is updated by
is updated by 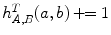 . Using a linear interpolation approach, the intensity is first interpolated,
. Using a linear interpolation approach, the intensity is first interpolated, 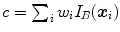 , and used to update the histogram
, and used to update the histogram 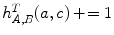 . Using the partial volume approach, the histogram is updated for four intensities
. Using the partial volume approach, the histogram is updated for four intensities 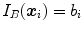 , with
, with 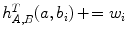 , which tends to give smoother histograms. The computed frequencies of joint intensities are normalized to the number of overlapping voxels
, which tends to give smoother histograms. The computed frequencies of joint intensities are normalized to the number of overlapping voxels 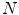 , resulting in the joint probabilities
, resulting in the joint probabilities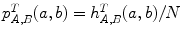 .
.Following the previous description, the size of the joint histogram matrix would be 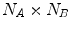 with
with 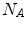 and
and 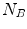 the number of different intensities in
the number of different intensities in 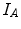 and
and 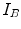 . In practice however, this would lead to large matrix sizes, which is why intensities are usually grouped into bins to reduce the size and enhance the statistics of the joint histogram.
. In practice however, this would lead to large matrix sizes, which is why intensities are usually grouped into bins to reduce the size and enhance the statistics of the joint histogram.
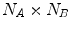 with
with 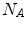 and
and 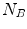 the number of different intensities in
the number of different intensities in 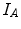 and
and 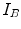 . In practice however, this would lead to large matrix sizes, which is why intensities are usually grouped into bins to reduce the size and enhance the statistics of the joint histogram.
. In practice however, this would lead to large matrix sizes, which is why intensities are usually grouped into bins to reduce the size and enhance the statistics of the joint histogram.
Fig. 6.3
2D illustration of the joint histogram updating process
For motion estimation of thoracic CT images, the two measures that have been frequently used are the sum of squared differences and mutual information, and we will focus on them first.
6.1.4.3 Sum of Squared Differences
The main advantage of computing the sum of squared differences (SSD) lies in its simplicity. It consists in summing the quadratic differences between the image intensities, voxel by voxel. The SSD can be computed from the joint histogram, 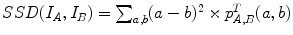 , but it is more efficient to not explicitly compute the joint histogram. Usually, the result is averaged over the amount of voxels
, but it is more efficient to not explicitly compute the joint histogram. Usually, the result is averaged over the amount of voxels  of the current overlap between the images
of the current overlap between the images  , to avoid favoring transformations that minimize the overlap,
, to avoid favoring transformations that minimize the overlap,
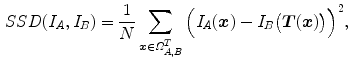
in which we assumed an interpolation scheme for evaluating 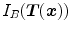 . It allows an easy expression of the derivatives and it is fast to compute. However, it assumes that the intensity distributions are similar in the two images and this assumption is violated when considering expiration to inspiration registration, due to the changes in lung density.
. It allows an easy expression of the derivatives and it is fast to compute. However, it assumes that the intensity distributions are similar in the two images and this assumption is violated when considering expiration to inspiration registration, due to the changes in lung density.
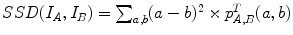 , but it is more efficient to not explicitly compute the joint histogram. Usually, the result is averaged over the amount of voxels
, but it is more efficient to not explicitly compute the joint histogram. Usually, the result is averaged over the amount of voxels 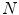 of the current overlap between the images
of the current overlap between the images 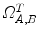 , to avoid favoring transformations that minimize the overlap,
, to avoid favoring transformations that minimize the overlap,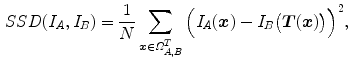
(6.3)
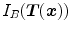 . It allows an easy expression of the derivatives and it is fast to compute. However, it assumes that the intensity distributions are similar in the two images and this assumption is violated when considering expiration to inspiration registration, due to the changes in lung density.
. It allows an easy expression of the derivatives and it is fast to compute. However, it assumes that the intensity distributions are similar in the two images and this assumption is violated when considering expiration to inspiration registration, due to the changes in lung density.Variants have been proposed, aimed at taking into account this lung density change. For example, Yin et al. [80] proposed to use the sum of squared tissue volume difference (SSTVD) to account for the preservation of the tissue mass of the lungs during respiration. Alternatively, pre-processing of the images has been proposed [57]. Similarity measures developed specifically for the lung are described in Chap. 7.
6.1.4.4 Mutual Information
Another measure that has been extensively used is the mutual information (MI) [37, 46, 74]
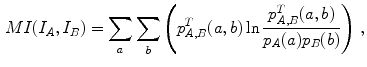
with 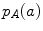 and
and 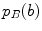 the probability of intensity
the probability of intensity 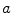 in image
in image 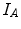 , and
, and 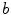 in image
in image 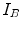 , and
, and 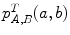 the joint probability for a given
the joint probability for a given  as described earlier.
as described earlier.
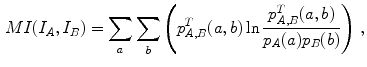
(6.4)
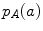 and
and 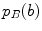 the probability of intensity
the probability of intensity 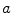 in image
in image 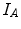 , and
, and 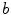 in image
in image 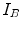 , and
, and 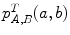 the joint probability for a given
the joint probability for a given 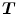 as described earlier.
as described earlier.The underlying idea is to measure the statistical dependence between the distributions of intensities of the two images. The link is quantified by an entropy measure. The entropy of a distribution 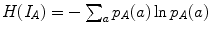 is a logarithmic measure of the density of states and can be considered as a measure of the uncertainty of the distribution: entropy is zero when one state is certain (
is a logarithmic measure of the density of states and can be considered as a measure of the uncertainty of the distribution: entropy is zero when one state is certain (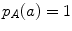 ) and is maximal when all events have the same probability.
) and is maximal when all events have the same probability.
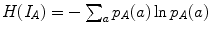 is a logarithmic measure of the density of states and can be considered as a measure of the uncertainty of the distribution: entropy is zero when one state is certain (
is a logarithmic measure of the density of states and can be considered as a measure of the uncertainty of the distribution: entropy is zero when one state is certain (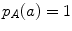 ) and is maximal when all events have the same probability.
) and is maximal when all events have the same probability.Given an intensity distribution, the mutual information can be interpreted as the decrease of uncertainty (or gain of information) brought by the knowledge of the second distribution (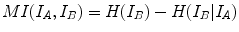 ). It can also be viewed as a distance between two 2D distributions: the current one composed of the joint image intensity probability given the current transformation (
). It can also be viewed as a distance between two 2D distributions: the current one composed of the joint image intensity probability given the current transformation (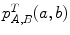 ), and the one corresponding to the case where there is a total independence of the two distributions (
), and the one corresponding to the case where there is a total independence of the two distributions (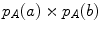 ). The further the joint probability from the total independence, the better the registration. The distance measure is called the Kullback-Leibler distance. A variant, the normalized mutual information (NMI) [65], normalizes the measure with respect to the image overlap and has shown to be less sensitive to changes in overlap.
). The further the joint probability from the total independence, the better the registration. The distance measure is called the Kullback-Leibler distance. A variant, the normalized mutual information (NMI) [65], normalizes the measure with respect to the image overlap and has shown to be less sensitive to changes in overlap.
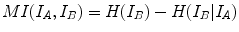 ). It can also be viewed as a distance between two 2D distributions: the current one composed of the joint image intensity probability given the current transformation (
). It can also be viewed as a distance between two 2D distributions: the current one composed of the joint image intensity probability given the current transformation (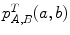 ), and the one corresponding to the case where there is a total independence of the two distributions (
), and the one corresponding to the case where there is a total independence of the two distributions (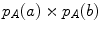 ). The further the joint probability from the total independence, the better the registration. The distance measure is called the Kullback-Leibler distance. A variant, the normalized mutual information (NMI) [65], normalizes the measure with respect to the image overlap and has shown to be less sensitive to changes in overlap.
). The further the joint probability from the total independence, the better the registration. The distance measure is called the Kullback-Leibler distance. A variant, the normalized mutual information (NMI) [65], normalizes the measure with respect to the image overlap and has shown to be less sensitive to changes in overlap.6.1.4.5 Other Similarity Measures
Other conventional measures for mono-modal image registration are the sum of absolute differences (SAD), or the linear correlation coefficient (LCC) which measures the of a linear relationship between the intensity distributions and is also widely used for registration of thoracic CT [82, 84]. For multi-modal cases, the correlation ratio (CR) [50] measures the strength of the dependency using the variance of the distributions.
Figure 6.4 illustrates three cases, where the variation in 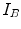 knowing
knowing 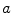 in
in 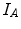 is measured in three different ways. LCC considers that the function
is measured in three different ways. LCC considers that the function 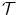 between the intensity distributions is a linear function.This is a stronger assumption on the link between the image intensities than in the case of CR and MI, which assume a functional relation and statistical dependence, respectively. MI considers the intensities like labels and thus any pairwise inversion of labels leads to the same value. CR is not a symmetric measure (
between the intensity distributions is a linear function.This is a stronger assumption on the link between the image intensities than in the case of CR and MI, which assume a functional relation and statistical dependence, respectively. MI considers the intensities like labels and thus any pairwise inversion of labels leads to the same value. CR is not a symmetric measure (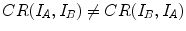 ) and one image must be chosen as the one which potentially explains the other image more. MI and LCC are symmetric measures.
) and one image must be chosen as the one which potentially explains the other image more. MI and LCC are symmetric measures.
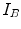 knowing
knowing 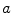 in
in 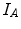 is measured in three different ways. LCC considers that the function
is measured in three different ways. LCC considers that the function 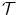 between the intensity distributions is a linear function.This is a stronger assumption on the link between the image intensities than in the case of CR and MI, which assume a functional relation and statistical dependence, respectively. MI considers the intensities like labels and thus any pairwise inversion of labels leads to the same value. CR is not a symmetric measure (
between the intensity distributions is a linear function.This is a stronger assumption on the link between the image intensities than in the case of CR and MI, which assume a functional relation and statistical dependence, respectively. MI considers the intensities like labels and thus any pairwise inversion of labels leads to the same value. CR is not a symmetric measure (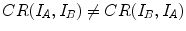 ) and one image must be chosen as the one which potentially explains the other image more. MI and LCC are symmetric measures.
) and one image must be chosen as the one which potentially explains the other image more. MI and LCC are symmetric measures.
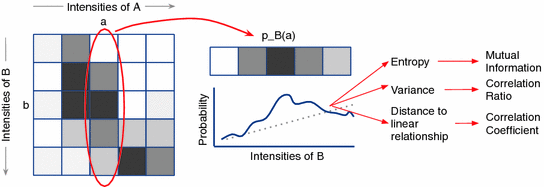
Fig. 6.4
Illustration of three different ways to measure uncertainty in the partial intensity probability distribution of intensity 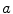 in
in 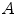 :
: 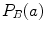
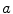 in
in 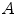 :
: 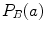
Deformable 2D-3D registration between CT and CBCT images is an emerging field of interest and measures have been proposed, specifically designed for this purpose. These include entropy of difference images, gradient correlation and pattern intensity. A review can be found in [38].
6.1.5 Regularization
In this section, we focus on the second term in Eq. (6.2). 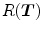 represents a regularization mechanism that penalizes undesirable properties of the transformation
represents a regularization mechanism that penalizes undesirable properties of the transformation 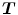 . Generally, regularizations are defined using an energy function and computed directly from the deformation field and independently of the image intensities. It constitutes an important tool to enforce a transformation model to the sought deformation, and incorporate prior knowledge into the registration framework.
. Generally, regularizations are defined using an energy function and computed directly from the deformation field and independently of the image intensities. It constitutes an important tool to enforce a transformation model to the sought deformation, and incorporate prior knowledge into the registration framework. 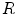 is often chosen to favor spatially smooth solutions, but any mathematical or physical property can be penalized, provided a penalty can be devised.
is often chosen to favor spatially smooth solutions, but any mathematical or physical property can be penalized, provided a penalty can be devised.
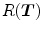 represents a regularization mechanism that penalizes undesirable properties of the transformation
represents a regularization mechanism that penalizes undesirable properties of the transformation 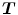 . Generally, regularizations are defined using an energy function and computed directly from the deformation field and independently of the image intensities. It constitutes an important tool to enforce a transformation model to the sought deformation, and incorporate prior knowledge into the registration framework.
. Generally, regularizations are defined using an energy function and computed directly from the deformation field and independently of the image intensities. It constitutes an important tool to enforce a transformation model to the sought deformation, and incorporate prior knowledge into the registration framework. 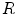 is often chosen to favor spatially smooth solutions, but any mathematical or physical property can be penalized, provided a penalty can be devised.
is often chosen to favor spatially smooth solutions, but any mathematical or physical property can be penalized, provided a penalty can be devised.It is advantageous to consider the transformation 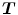 as the sum of the identity transformation and a displacement function
as the sum of the identity transformation and a displacement function 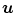 , i.e.
, i.e.
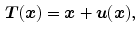
as most regularization energies will only be affected by the displacement.
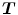 as the sum of the identity transformation and a displacement function
as the sum of the identity transformation and a displacement function 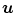 , i.e.
, i.e.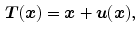
(6.5)
The linear elastic energy is commonly used for registration [14]:
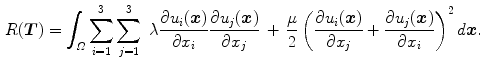
It is based on the physical equations of the deforming material, assuming that the relationship between strain and stress is linear. Viscous fluid energy [1, 2, 5] has the same equations as the linear elastic energy, but computed for the velocity field (the increment in each iteration to the transformation) instead of the deformation field.
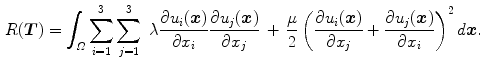
(6.6)
The membrane or Laplacian energy,
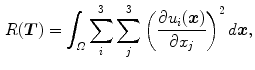
can be considered as a simplification of the linear elastic energy where the cross-directional effects are ignored.
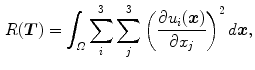
(6.7)
Bi-harmonic energy [4],
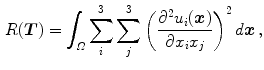
also known as bending energy or second-order Tikhonov stabilizer, is another popular regularization energy which penalizes non-affine transformations. Note that this quantity is the 3D counterpart of the 2D bending energy of a thin plate of metal. Thin-plate splines commonly used in feature-based registration approaches (see Sect. 5.4.2) correspond to an exact solution of this energy minimization.
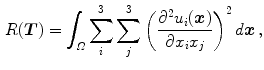
(6.8)
Several authors proposed regularizations based on the Jacobian [32, 51], including:
[32, 51], including:
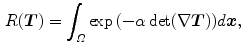 < div class='tao-gold-member'>
< div class='tao-gold-member'>




 [32, 51], including:
[32, 51], including: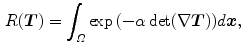
Only gold members can continue reading. Log In or Register to continue
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


