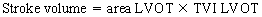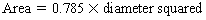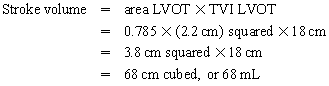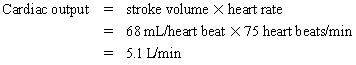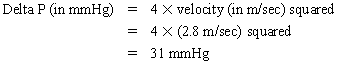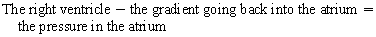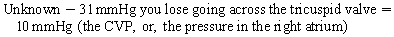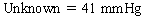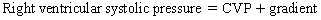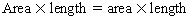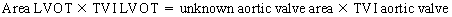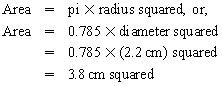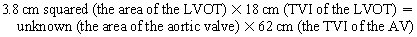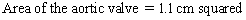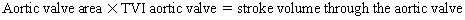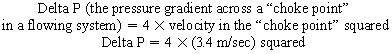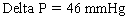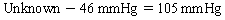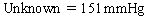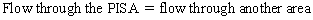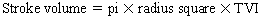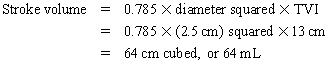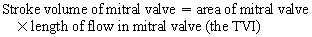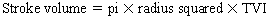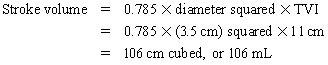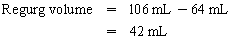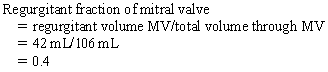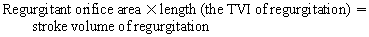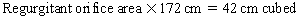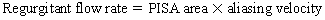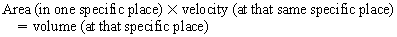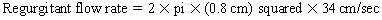Hemo-dynamo Doc

The Bernoulli equation will appear a million times in any discussion of TEE. The complicated form of this equation takes Sir Isaac Newton to decipher, but the simplified version comes to us as the digestible.

Delta P (the change in pressure between two chambers in a flowing system) = 4 × velocity squared (where the velocity is measured at a “choke point” or narrowing between the two chambers)

So picture the place we’re interested in measuring, here the right ventricle. Where is there a “choke point” or narrowing that leads into or out of the right ventricle, we can measure a velocity. (Remember, the TEE can measure a velocity for you, but it cannot measure a pressure.)

Aha! The patient has tricuspid regurgitation, and there is a measurement of the tricuspid regurg velocity that we can measure:

(Note well, the units for the Bernoulli equation work out as follows—use the velocity in m/sec and your gradient will come out in mmHg.)

So let’s convert that TR velocity into a gradient:

Now on to the second thing you need to solve this problem.

The Commonsensical/Visual

So we want to know the pressure in one place, we have a gradient, and we have a pressure in a second place. Here’s where the common sense comes in.

There is a higher pressure place, the right ventricle (that’s what contracts, after all). There is a lower pressure place, the atrium (the pressure in that thin-walled chamber better be lower than the thicker walled ventricle).

Common sense tells you that you could set up an equation like this:

In the TEE review course, they said:

This may work for you, but I found it more useful to think through the problem from the vantage of “here’s the high-pressure area, here’s the low-pressure area, and here’s the loss of pressure between them”. That way you’ll understand the way the pressure works, and you’ll be less likely to, say, subtract the CVP from the gradient rather than add the CVP to the gradient. Once you’re done, you can then draw your picture and see if common sense holds up.

Calculation of Peak Aortic Valve Area

Here the continuity equation comes home to roost. At first baffling, the continuity equation makes sense: it’s just a question of cross multiplying and dividing, and shouldn’t make you lose much sleep.

Why bother? Why not just draw a line around the open aortic valve and let the TEE machine do the area for you by planimetry?

Ah, grasshopper, things are not so simple as they seem.

Planimetry, as so many things in life, only works when you don’t need it! (Kind of like the umbrella that never leaks unless it rains, or the life preserver that doesn’t let you drown unless you happen to fall into the ocean.) When the aortic valve is crunchy and stenotic, planimetry (a two-dimensional exercise), just cannot get a good handle on the exact orifice area. You outline up here, but there is more stenosis below your outline, or there is more stenosis above your planimetry, so the planimetry is just no good.

Continuity Equation Idea: flow through one area of the heart equals flow through another area of the heart.

Fluids are not compressible, so you can’t “squish” the blood. Also, blood cannot just “disappear”, which brings up the BIG EXCEPTION to the continuity equation:

If a patient has noncontinuous flow (septal defect somewhere), then you can’t use the continuity equation. To use continuity, have continuity!

So, if you can measure flow through one area, then that should equal flow in another area.

Flow here = flow there. The essence of the continuity equation.

Recall from earlier that we “create” measurable flow by assuming a cylindrical amount of blood flow. (We did that in the original part of this problem, the stroke volume problem. Go back now and nail that down, because that is the heart of the continuity equation.) We measure this cylindrical flow by getting one area and multiplying it by the length (the time-velocity integral), thus getting flow.

We know we want to know the aortic valve area, so where can we find another place to measure stuff?

The left ventricular outflow tract, of course! (The LVOT is forever bailing our mathematical asses out of trouble.)

So flow through the LVOT should equal flow through the aortic valve. So plug in the respective three things that we DO have, and solve for the one thing we don’t have:

You have the diameter of the LVOT, 2.2 cm, so use the area formula:

So, plodding along,

Cross multiply and divide, solving for the area of the aortic valve, and, voila!

Does this pass the units test? Yes. Aortic valve areas are measured in cm squared.

Does this pass the common sense test? Yes, this fits the general size you would expect of a stenotic aortic valve. You didn’t get an aortic valve area the size of an electron, nor did you get an area the size of Comiskey Park.

Now hold on to your slide rulers and cyclotrons—there is, it turns out, another way to get the aortic valve area.

Go back to the cylinder of blood idea (the gist of all these equations). If you look just at the aortic valve, you could say:

So, if you were of a mind to, you could calculate the aortic valve area that way, could you not? (The first time you see this, you’ll go, “Huh? Aren’t they cheating?”.) But it’s actually not cheating, because, in order to get the stroke volume, you had to use the concept of the “cylinder of blood going through the LVOT” (see above, where we calculated the very first part of this problem, the stroke volume).

Take a second to digest this.

No, really, look back up there, don’t take this on faith.

Satisfied? Good.

So, here we go with the second way to calculate the area of the aortic valve.

Cross multiply and divide, and gee whiz golly, the aortic valve area is still 1.1 cm squared.

That shouldn’t surprise you, as this patient hasn’t aged much during this problem.

What should surprise you is a second answer different from your first. Since you were just grinding the same numbers through in different ways, you should get a second answer the same as the first. If you don’t, go back and rework it.

Calculation of Peak Aortic Valve Gradient

A little less Sturm und Drang here. Just use the Bernoulli equation:

(Keep in mind, you need that velocity in m/sec to get a pressure in mmHg!)

Calculation of Peak Left Ventricular Pressure

At the TEE course, they didn’t ask for this, but it’s worth doing just to get that “high-pressure area, gradient loss, low-pressure area” idea down.

First, draw a picture of what you’re trying to find. (To repeat, getting the concept down of where the high pressure should be, as well as where the low pressure should be, is important. A good picture will make sure you add where you should add and subtract where you should subtract.)

The high-pressure area should be the left ventricle in systole, because the left ventricle has to overcome the “choke point” of the aortic valve, and still have enough oomph left over to provide systolic pressure.

High pressure in the left ventricle (unknown) − pressure lost in the stenotic aortic valve (the previously calculated gradient of 46 mmHg) = pressure left over in the aorta (the systolic pressure of 105 mmHg)

Now, redraw the picture and see if it makes sense.

Case 2

48-yo man having CABG. Monitoring includes a finger on the pulse and an anesthesiologist on the phone to Merrill-Lynch. OK, OK, sorry. Monitoring includes an A-line, CVP, and TEE. LV appears dilated and hypocontractile. There is a central jet of MR judged to be 2+ to 3+ in severity. The following measurements are made:

• Diameter LVOT: 2.5 cm

• TVI LVOT: 13 cm

• Mitral annular diameter: 3.5 cm

• TVI mitral annular diameter: 11 cm

• PISA radius: 0.8 cm

• PISA alias velocity: 34 cm/sec

• Peak velocity MR: 574 cm/sec

• TVI MR: 172 cm

Calculate the following:

• LVOT stroke volume

• MV stroke volume

• MV regurgitant volume

• MV regurgitant fraction

• Regurgitant orifice area

• PISA calculations

• Regurgitant flow rate

• Regurgitant orifice area

• Regurgitant volume

• Regurgitant fraction

Before you regurgitate yourself at all this stuff, a few pointers.

On this, the math part of the test, they will just give you the various measures. They’ll lay LVOT diameter on a silver platter and hand it to you. In other parts of the test, you will visually have to show exactly where you would take this measurement yourself. And on the test the various places are damned close to one another, so make sure you know where to take these measurements.

Second, PISA makes the whole auditorium groan, it seems so esoteric at first. But once you gird your loins and throw yourself into this stuff, you’ll see that PISA is just the continuity equation in another form.

PISA’s area is a hemisphere, so that’s a little different.

PISA’s area is affected by its angle to the valve, so that’s a little different.

PISA implies you know what the hell aliasing is, so that’s a little different.

Alright, so PISA is a pain in the ass, what can I tell you? I didn’t make up the exam!

Let’s take a little breather from the PISA monster, get as far along as we can in the calculations, get a little confidence, then jump into the snake pit of PISA-ness.

Calculation of LVOT Stroke Volume

Whew, this is review. If you got the karma of the first case, this should be cake. I’ll go through it just as slowly, though, so we jam this stuff into your sulci but good.

From the chaos and irregularity of a real-live stroke volume, we make up a “pretend” stroke volume that magically looks like a perfect cylinder, with a perfect area and length.

Next, we look at the LVOT, make our area calculation, then multiply it by the length (the TVI):

Or, in TEE Course-speak:

Units make sense? Yes. Common sense rule checks out? Yes. (Make it a habit to always do this two-part checkout.)

Calculation of MV Stroke Volume

Danger! Danger, Will Robinson! Remember, when you measure these, to measure both the diameter and the TVI at the same place. In this problem, be sure to measure both the diameter of the mitral valve and the TVI of the mitral valve at the annulus. If you measure the diameter at the annulus and the TVI at, say, the tips of the mitral valve, then you would get an inaccurate result.

So once again, we are invoking a “cylinder of blood flow”.

Though the mitral valve is more like an oval, for purposes of this problem, we will consider it a circle:

Or, bowing to TEE convention:

Units check? Yes. Common sense check? Wait a minute! Didn’t we just calculate an LVOT stroke volume of 64 mL? Now where did this stroke volume of 106 mL come from? What about the Holiest of Holies, the continuity equation?

Confused? Pause for a moment and think about what’s happening.

This patient has mitral regurgitation, so it makes sense that more should go through the mitral valve than goes out the LVOT. Some of that mitral volume is lost by going backward (as we’ll see below). Recall, too, that the continuity equation doesn’t apply here, because the LVOT measurement applies to blood flowing out to the aorta during systole. The blood flow going forward through the mitral valve occurs during diastole.

Systole and diastole do not occur at the same time. They are DIScontinuous so the continuity equation does not apply to them.

So, in review, the units check and the common sense also checks, once you think about what is happening and when it is happening.

Calculation of MV Regurgitant Volume

Now it starts to come together.

Regurgitant volume through the mitral valve = total volume that goes through the mitral valve – total volume that goes out through the aortic valve

Another warning for Will Robinson.

This calculation only holds if there is no aortic regurgitation as well. The extra flow that comes back during aortic regurgitation would mix in with the blood regurgitating through the mitral valve, and all bets are off on volume calculations.

Adding aortic regurg to mitral regurg takes you from one equation–one unknown to one equation–two unknowns, and that is a no-no.

Units check? Yes. Common sense check? Ye-e-e-es. (If you find yourself hesitating, draw a picture to satisfy yourself that it does, indeed, make sense.)

Calculation of MV Regurgitant Fraction

No rocket science here.

or, in percentage terms, regurgitant percentage = 40%.

Units check? Yes, there are no units.

Common sense check? Yes, you can see a regurgitant valve tossing 40% backward. That goes along with significant regurg.

You’ll note you didn’t come up with something impossible, like a regurgitant percentage of 178% or a regurgitant percentage of −5%. Thank heaven for small miracles.

Calculation of Regurgitant Orifice Area

This is a little hypothetical, as the regurgitant orifice area is not a fixed thing that instantly appears, then instantly disappears. In reality, it’s more like a door that is closed, opens at a certain speed, stays open for a length of time, and then closes at a certain speed. This calculation looks at the “door all the way open” and ignores the reality of the “opening period” and the “closing period”.

But you’re not here to think. Just do the calculation and keep your trap shut.

Go back to our cylinder of blood and start calculating.

Cross multiply and divide, you busy little hemodynamic beavers.

Units check? Yep. Common sense check? U-u-uh.

That makes sense. The mitral valve isn’t a complete waste case; it is regurgitant, but not wide, wide open, so it makes sense that a portion, not all, of the valve effectively “stays open” during systole, allowing for the 40% regurgitation.

PISA Calculations

Hunker down, cowboys and cowgirls, it’s not so bad as you think. Before we go into the actual calculations in this case, let’s go over the main aspects of PISAtology.

Look at the words that make up PISA, and draw pictures to illustrate the point.

Proximal. That means the colorful and troublesome PISA radius will appear on the upstream part of the “choke point”. So draw a few pictures. If the patient has mitral regurg, and the flow is pouring from the high-pressure left ventricle into the low-pressure left atrium, the PISA will appear where?

Proximal! That is, the PISA will appear in the left ventricle, the “near” side of the “choke point”. The proximal area of the choke hold, not the far side. That would be “distal isovelocity surface area”, and if you think of the chaotic flow on the far side of a “choke point”, that doesn’t make sense.

How about a case of mitral stenosis? Flow is trying to “squeeze” through a tight mitral valve. Where would the PISA radius appear then?

Proximal! On the near side of the choke point, that is, in the left atrium.

Again, a radius on the far side of the choke point doesn’t make sense.

Isovelocity. All the flow at that area is the same. Recall that flow Doppler is a pulsed-wave, not a continuous-wave, phenomenon. At a certain velocity, the color of the wave will change. Conveniently for us, the aliasing velocity (the velocity where color change occurs) is listed on the machine.

Well, why should the isovelocity thing line up so perfectly for us. Why isn’t the isovelocity thing scattered all over the map?

Think of water going toward a narrow sluice gate. The velocities are all over the map, until you get real close; then the pressure bearing down on the water is all the same. The velocities “organize” as the water gets closer to the sluice gate, and you get a hemisphere of water all going the same speed toward that narrow opening. That is why you get a hemisphere of “isovelocity-ness” that appears on the TEE screen.

Surface Area. Unlike earlier equations, which used the area of a circle (pi × radius squared), this area is that of a hemisphere (2 × pi × radius squared). Why? Look at the PISA thing. It is a hemisphere, not a circle.

So that’s where you get the 2 × pi × radius squared. In calculations done at the conference, they give you the radius and you go with 6.28 (that is, 2 × 3.14) × radius squared.

So, once you believe in PISA, have the formula for area of a hemisphere down, and recall the continuity equation, you are in business.

Calculation of Regurgitant Flow Rate by PISA

Just as in other valve calculations, invent the idea of a cylinder of blood flowing along with a certain area and a certain length. This requires a little mind bending, as you are used to looking at the area of a circle and multiplying it by the length. Here, with PISA calling the shots, you make an area of a hemisphere and multiply it by the length.

Try not to think about it too much, you might pop an aneurysm. Just go with the flow.