, Tobias Klinder1 and Jens von Berg1
(1)
Philips Research Laboratories, Hamburg, Germany
Abstract
In contrast to intensity-based image registration, where a similarity measure is typically evaluated at each voxel location, feature-based registration works on a sparse set of image locations. Therefore, it needs an explicit step of interpolation to supply a dense deformation field. In this chapter, the application of feature-based registration to pulmonary image registration as well as hybrid methods, combining feature-based with intensity-based registration, is discussed. In contrast to pure feature based registration methods, hybrid methods are increasingly proposed in the pulmonary context and have the potential to out-perform purely intensity based registration methods. Available approaches will be classified along the categories feature type, correspondence definition, and interpolation type to finally achieve a dense deformation field.
Keywords
Feature-based registrationAnatomical featuresGray value featuresPoint correspondenceDeformation interpolation5.1 Introduction
Probably the most intuitive approach to find a suitable transformation bringing two images into the same frame of reference, is by means of a set of corresponding points. In principle, they could be defined manually. But since we want to define a non-rigid registration, needing perhaps hundreds or thousands of points for a decent deformation field, we will concentrate on automated procedures. We will discuss how suitable feature points can be found, how point correspondence in two images can be established, and how a transformation can finally be estimated. Still, we have a sparse point set in mind, associated with a specific feature, be it a vessel bifurcation or a characteristic gray value structure. This is in contrast to the so called intensity based registration which will be discussed in Chaps. 6 and 7. Intensity based image registration treats typically each image location equally. For every grid position or voxel in a source image, the corresponding location in a target image is found by evaluating a suitable intensity based similarity measure. Most medical images, however, contain more or less homogeneous regions with no or little gray value contrast. This makes the above task of finding correspondence an ill-posed problem. It is commonly solved by either applying explicit smoothness constraints to the deformation field or by exploiting implicit smoothness introduced by the specific parameterization of the deformation field. In effect, the behavior of an intensity-based registration is mainly characterized by matching image regions with suitable contrast and performing an implicit or explicit interpolation in between.
The feature-based registration, however, explicitly attempts to register only highly structured image regions and to obtain a dense deformation field by interpolating the resulting sparse deformation vector field. A considerable variety of methods has been proposed, differing in feature type, and how feature correspondence is established. In addition, hybrid methods have been proposed, combining feature-based and intensity-based registration.
We classify feature-based registration algorithms based on the following categories:
Consequently, the rest of this chapter is organized along these categories. Feature-based registration was very frequently used to estimate rigid or affine transformations. Here, we focus on non-linear transformations, for which feature-based registration was pioneered for the purpose of brain registration. In the context of a comparison of algorithms for pulmonary image registration, performed at a satellite workshop of the 13th International Conference on Medical Image Computing and Computer Assisted Intervention (MICCAI 2010), actually none of the high-ranking methods was a purely feature-based method. However, a few of them, including the winner [19] of the online-contest, were hybrid methods, combining intensity with feature-based registration. The feature part of those hybrid methods will also be discussed in this chapter. Table 5.1 contains an overview of feature-based and hybrid non-rigid registration approaches for pulmonary applications. In this chapter, we focus on feature-based registration for lung motion estimation and not on the registration of surrounding structures, such as vertebrae and ribs, for which we only give the work of Matsopoulus (item 2 in Table 5.1) as an example. The authors attempt here to achieve a registration of the lung region of interest independent of the breathing phase.
Feature type, which includes feature dimension (point, line, surface) and feature characterization (e.g. bifurcation-point, vessel-centerline, ridge-line of a surface, or other intensity patterns)
Feature correspondence definition (e.g. anatomical labeling, 3D Shape Context, current-based, shaped-constrained deformable models)
Interpolation type for generating dense deformation fields.
Table 5.1
Classification of feature-based registration for pulmonary applications
Author | Year | Feature | Correspondence | Interpolation | |
|---|---|---|---|---|---|
1 | C.V. Stewart et al. [32] | 2004 | Points, lines, and surfaces | Modified ICP | B-spline-based |
2 | G.K. Matsopoulos et al. [28] | 2005 | Points: vertebrae, ribs, shoulder | Self organizing maps | RBF (shifted log) |
3 | M. Urschler and H. Bischof [33] | 2005 | Surface: lung surface | Shape context | TPS |
4 | A. Hilsmann et al. [21] | 2007 | Points: vessel tree bifurcations | Shape context | TPS |
5 | T. Klinder et al. [24] | 2008 | Surfaces: lung surf. and inner structures | Shape constrained deformation | TPS |
6 | Y. Huang et al. [22] | 2009 | Points, and lines: bronchial tree, bifurcation points | Hufman code | TPS and Demons |
7 | V. Gorbunova et al. [17] | 2009 | Lines, surfaces: vessel tree, lung surface | Currents-based registration | Gaussian kernel diffeomorphic matching |
8 | K. Cao et al. [6] | 2010 | Lines: vessel tree | Via hybrid registration | Via hybrid registration |
9 | D. Loecks et al. [25] | 2010 | Points: vessel bifurcations | Local and global correspondence model | Via hybrid registration |
10 | X. Han [19] | 2010 | Points: Förstner operator | SURF descriptor | Via hybrid registration |
Feature-based registration approaches can provide a natural way to treat motion field discontinuities, for example at the lung pleura, by separate registration of feature sub-sets, e.g., pulmonary structures and ribs. This is similar to a regionally restricted intensity-based registration, but does not require an accurate region segmentation. The problem, however, how to interpolate a dense motion field for the full image domain persists.
5.2 Feature Types
Feature-based registration does not necessarily mean that a point-wise correspondence between landmarks is established, meaning that at the landmark position all degrees of freedom (DOF) for the deformation field are removed. By registration of line-like features such as vessels or bronchial branches only DOF across the line are removed. This leaves one DOF along the line. Similarly, surfaces like the pleura or the lung fissures locally remove only one DOF and leave two DOF on the surface. However, even in the case of line or surface features, often in a successive step, a virtual point-to-point correspondence is established with suitable mapping approaches, such as the iterative closest point (ICP) or related algorithms [3, 12]. Features may be determined as anatomical objects, or by their gray value structure, independent from the anatomy. Examples are, e.g., a bronchial or vascular bifurcation point, or a point with high gray value variability in all three spatial directions.
5.2.1 Anatomical Features
If an anatomical feature can be identified in both images as a unique anatomical landmark, the correspondence problem becomes trivial. In addition, anatomical features are easy to handle in interactive definition or correction schemes. For the registration of the thorax, anatomical objects surrounding the lungs, such as vertebrae and ribs can be used if an independence from the breathing phase is [28] intended. For the estimation of pulmonary motion, however, the surface of the lungs, fissures, bronchial and vascular tree can be used.
Regarding the lung surface, it can be assumed that the motion of it, can to some extent serve as a predictor of the internal lung motion. This is especially the case in the region around the diaphragm. Furthermore, most of the intensity based registration algorithms need as input a delineation of the lungs in order to properly handle the motion discontinuities at the lung borders. While automated lung segmentation is a fairly easy task (at least in the absence of gross pathologies), it is less straight forward to establish anatomical correspondence on the lung surface. In Sects. 5.3.4, 5.3.5, and 5.3.6 approaches to solve the correspondence problem for the lung surface will be discussed.
Further candidates are bronchi and blood vessels. The distal portions of bronchial and vascular trees in the lungs are inaccessible for anatomical identification due to inter-patient variability, the obscuring influences of noise and image artifacts, and the sheer amount of structures such as small branches or bifurcations. Still, these structures can be detected and used as input for feature-based registration.
A weak feature influence within a hybrid registration method was introduced by Cao et al. [6], by adding a ‘vesselness’-based [13] similarity measure. With weak in this context we mean that no explicit point-to-point correspondence is established. The approach increases the probability that vessels are registered to vessels, without the need to establish explicit correspondence between the vessel trees to be matched. The additional similarity measure follows Frangi’s proposal of using the Eigenvalues of the Hessian matrix to extract curvi-linear image structures in 2D and 3D images. The approach is on the borderline between feature based and intensity based registration. It can be argued that just an additional similarity measure is introduced in an intensity based registration algorithm and that no explicit correspondences are established. On the other hand, image regions are treated differently, depending on the appearance of vessel-like features. Loeckx et al., again in the context of a hybrid registration approach, determined a set of corresponding vessel bifurcation points in fixed and moving image and used them in an additional similarity measure [25]. In a pre-processing step, a set of bifurcations points is generated in both images using a threshold-based segmentation and sub-sequent skeletonization of the pulmonary vessel tree. In addition, the correspondence between the bifurcation points in both images is established (see Sect. 5.3). During the iterations of the hybrid registration, the Euclidean distance between bifurcation points in the fixed image and transformed corresponding points in the moving image is used in addition to a mutual information-based similarity measure.
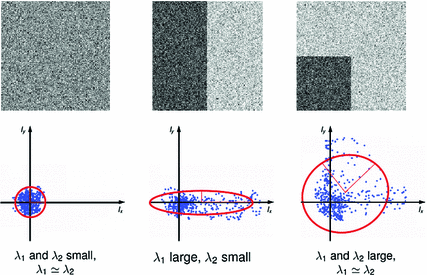

Fig. 5.1
Illustration of the structure tensor for three artificial 2D cases with (i) no predominant (left), (ii) one predominant (middle), and (iii) two predominant (right) gradient directions. The Eigenvectors and values 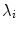 of the structure tensor can be interpreted as direction and length of the principal axes of an ellipsoid fitted to the distribution. Figure from Goldlücke [16]
of the structure tensor can be interpreted as direction and length of the principal axes of an ellipsoid fitted to the distribution. Figure from Goldlücke [16]
 of the structure tensor can be interpreted as direction and length of the principal axes of an ellipsoid fitted to the distribution. Figure from Goldlücke [16]
of the structure tensor can be interpreted as direction and length of the principal axes of an ellipsoid fitted to the distribution. Figure from Goldlücke [16]5.2.2 Gray Value Structure Features
In contrast to anatomically motivated features, it is also possible to search for gray value structures that are on the one hand characteristic enough to allow a good localization and that on the other hand provide a better lung coverage in the distal regions of bronchial and vascular tree. A standard approach for this idea is the analysis of the gradient structure of a small image region, as given by an averaged structure tensor. The structure tensor is the tensor product of the image gradient 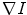 with itself. The Eigenvalues of the averaged structure tensor
with itself. The Eigenvalues of the averaged structure tensor 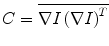 are characteristic for the type of structure in the covered region as depicted in Fig. 5.1. Three Eigenvalues that are large in magnitude are required for a characteristic landmark, because this indicates intensity variation in all directions. Consequently, a variety of formulas based on the product of the Eigenvalues of
are characteristic for the type of structure in the covered region as depicted in Fig. 5.1. Three Eigenvalues that are large in magnitude are required for a characteristic landmark, because this indicates intensity variation in all directions. Consequently, a variety of formulas based on the product of the Eigenvalues of 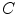 as given by the determinant, by the sum of the Eigenvalues as given by the trace of
as given by the determinant, by the sum of the Eigenvalues as given by the trace of 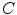 have been proposed as feature point detectors (see [20] for an overview and comparison). Han [19] determined local maxima of the structure tensor-based Förstner operator
have been proposed as feature point detectors (see [20] for an overview and comparison). Han [19] determined local maxima of the structure tensor-based Förstner operator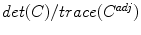 [20] as feature points and established point correspondence using SURF descriptors [1] (see Sect. 5.3). In a hybrid registration setup, the quadratic distance between the resulting feature-based transformation field and the current estimated transformation field was used in addition to a mutual information and a curvature penalizing term during the hybrid registration iterations.
[20] as feature points and established point correspondence using SURF descriptors [1] (see Sect. 5.3). In a hybrid registration setup, the quadratic distance between the resulting feature-based transformation field and the current estimated transformation field was used in addition to a mutual information and a curvature penalizing term during the hybrid registration iterations.
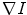 with itself. The Eigenvalues of the averaged structure tensor
with itself. The Eigenvalues of the averaged structure tensor 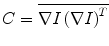 are characteristic for the type of structure in the covered region as depicted in Fig. 5.1. Three Eigenvalues that are large in magnitude are required for a characteristic landmark, because this indicates intensity variation in all directions. Consequently, a variety of formulas based on the product of the Eigenvalues of
are characteristic for the type of structure in the covered region as depicted in Fig. 5.1. Three Eigenvalues that are large in magnitude are required for a characteristic landmark, because this indicates intensity variation in all directions. Consequently, a variety of formulas based on the product of the Eigenvalues of 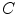 as given by the determinant, by the sum of the Eigenvalues as given by the trace of
as given by the determinant, by the sum of the Eigenvalues as given by the trace of 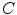 have been proposed as feature point detectors (see [20] for an overview and comparison). Han [19] determined local maxima of the structure tensor-based Förstner operator
have been proposed as feature point detectors (see [20] for an overview and comparison). Han [19] determined local maxima of the structure tensor-based Förstner operator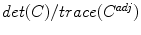 [20] as feature points and established point correspondence using SURF descriptors [1] (see Sect. 5.3). In a hybrid registration setup, the quadratic distance between the resulting feature-based transformation field and the current estimated transformation field was used in addition to a mutual information and a curvature penalizing term during the hybrid registration iterations.
[20] as feature points and established point correspondence using SURF descriptors [1] (see Sect. 5.3). In a hybrid registration setup, the quadratic distance between the resulting feature-based transformation field and the current estimated transformation field was used in addition to a mutual information and a curvature penalizing term during the hybrid registration iterations.5.3 Feature Correspondence
In the case of unique anatomical landmarks, the feature correspondence is trivially given. If this is not the case, correspondence has to be either explicitly established in an additional processing step or implicitly, e.g., by combining the feature-based procedure with an intensity-based registration into a hybrid registration approach. Often, even for named line or surface features, where correspondence of the whole anatomical structure is given, a point-wise correspondence between point sets distributed on the pair of lines or surfaces is established. The main approaches for establishing correspondence are described in the following.
5.3.1 Iterative Closest Point and Modifications
The iterative closest point (ICP) was initially presented by Besl in [3]. Its main idea is to establish a correspondence between two point clouds 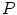 and
and 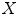 by performing the following four steps (i) compute for each
by performing the following four steps (i) compute for each 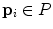 the closest point from
the closest point from 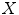 , (ii) compute a transformation to match
, (ii) compute a transformation to match 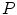 to
to 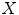 , (iii) apply the transformation to all points in
, (iii) apply the transformation to all points in 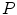 , (iv) repeat (i)–(iii) until convergence. Initially, it was assumed that the transformation between the two point clouds could be described by a rigid transformation so that step (iii) could be found in a closed form solution. It has to be noted that
, (iv) repeat (i)–(iii) until convergence. Initially, it was assumed that the transformation between the two point clouds could be described by a rigid transformation so that step (iii) could be found in a closed form solution. It has to be noted that 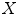 does not necessarily have to be a discrete point cloud but could also be a line or surface. Various extensions have been presented to allow non-rigid transformations between the two point clouds (see e.g., [12]). Although the ICP states a very standard algorithm for finding a correspondence between two point sets as it is fast and accurate in many cases, it is a method minimizing a non-convex cost function, and thus it lacks in terms of robustness w.r.t. the initial transformation because of local minima. Furthermore, the computation time is proportional to the number of points, which can be prohibitive when registering two large sets of points. For that reason, many approaches exist addressing robustness, e.g., using a random sampling of points at each iteration, bidirectional distance measurements, remove outliers, or introducing probabilities, and speed, e.g., using
does not necessarily have to be a discrete point cloud but could also be a line or surface. Various extensions have been presented to allow non-rigid transformations between the two point clouds (see e.g., [12]). Although the ICP states a very standard algorithm for finding a correspondence between two point sets as it is fast and accurate in many cases, it is a method minimizing a non-convex cost function, and thus it lacks in terms of robustness w.r.t. the initial transformation because of local minima. Furthermore, the computation time is proportional to the number of points, which can be prohibitive when registering two large sets of points. For that reason, many approaches exist addressing robustness, e.g., using a random sampling of points at each iteration, bidirectional distance measurements, remove outliers, or introducing probabilities, and speed, e.g., using 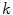 –
–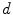 trees and/or closest point caching. However, even with latest modifications, robustness and speed are still critical when applying the ICP.
trees and/or closest point caching. However, even with latest modifications, robustness and speed are still critical when applying the ICP.
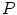 and
and 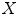 by performing the following four steps (i) compute for each
by performing the following four steps (i) compute for each 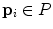 the closest point from
the closest point from 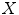 , (ii) compute a transformation to match
, (ii) compute a transformation to match 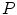 to
to 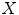 , (iii) apply the transformation to all points in
, (iii) apply the transformation to all points in 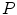 , (iv) repeat (i)–(iii) until convergence. Initially, it was assumed that the transformation between the two point clouds could be described by a rigid transformation so that step (iii) could be found in a closed form solution. It has to be noted that
, (iv) repeat (i)–(iii) until convergence. Initially, it was assumed that the transformation between the two point clouds could be described by a rigid transformation so that step (iii) could be found in a closed form solution. It has to be noted that 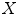 does not necessarily have to be a discrete point cloud but could also be a line or surface. Various extensions have been presented to allow non-rigid transformations between the two point clouds (see e.g., [12]). Although the ICP states a very standard algorithm for finding a correspondence between two point sets as it is fast and accurate in many cases, it is a method minimizing a non-convex cost function, and thus it lacks in terms of robustness w.r.t. the initial transformation because of local minima. Furthermore, the computation time is proportional to the number of points, which can be prohibitive when registering two large sets of points. For that reason, many approaches exist addressing robustness, e.g., using a random sampling of points at each iteration, bidirectional distance measurements, remove outliers, or introducing probabilities, and speed, e.g., using
does not necessarily have to be a discrete point cloud but could also be a line or surface. Various extensions have been presented to allow non-rigid transformations between the two point clouds (see e.g., [12]). Although the ICP states a very standard algorithm for finding a correspondence between two point sets as it is fast and accurate in many cases, it is a method minimizing a non-convex cost function, and thus it lacks in terms of robustness w.r.t. the initial transformation because of local minima. Furthermore, the computation time is proportional to the number of points, which can be prohibitive when registering two large sets of points. For that reason, many approaches exist addressing robustness, e.g., using a random sampling of points at each iteration, bidirectional distance measurements, remove outliers, or introducing probabilities, and speed, e.g., using 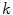 –
–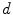 trees and/or closest point caching. However, even with latest modifications, robustness and speed are still critical when applying the ICP.
trees and/or closest point caching. However, even with latest modifications, robustness and speed are still critical when applying the ICP.5.3.2 Shape-Based Descriptors
The ‘Robust Tree Registration’ approach described by Loeckx et al. [25] uses the distance between corresponding vessel tree bifurcation points as an additional similarity measure in a hybrid registration approach. Correspondence is established by means of internal distances between any pair of points. Two distance measures, namely Euclidean and Geodesic distance (shortest path along the tree skeleton) are used separately. Using a Gaussian distribution model, a distance-based matching probability 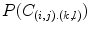 is calculated for the occurrence
is calculated for the occurrence 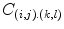 , that two point-pairs
, that two point-pairs 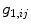 and
and 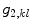 found in fixed and moving image respectively, do match.
found in fixed and moving image respectively, do match.
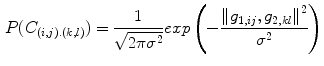
By marginalization, matching probabilities for any two points in fixed and moving image can be found:
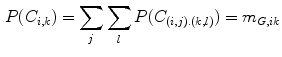
The authors calculate Geodesic 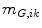 and Euclidean
and Euclidean 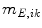 probabilities according to (5.2) and additionally a gray value-based correspondence probabilitiy (see next sub-Sect.). The product of the three is used to finally establish hard correspondences between feature points in fixed and moving image.
probabilities according to (5.2) and additionally a gray value-based correspondence probabilitiy (see next sub-Sect.). The product of the three is used to finally establish hard correspondences between feature points in fixed and moving image.
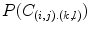 is calculated for the occurrence
is calculated for the occurrence 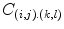 , that two point-pairs
, that two point-pairs 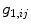 and
and 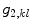 found in fixed and moving image respectively, do match.
found in fixed and moving image respectively, do match.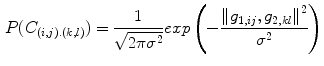
(5.1)
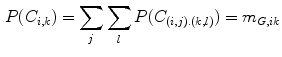
(5.2)
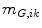 and Euclidean
and Euclidean 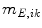 probabilities according to (5.2) and additionally a gray value-based correspondence probabilitiy (see next sub-Sect.). The product of the three is used to finally establish hard correspondences between feature points in fixed and moving image.
probabilities according to (5.2) and additionally a gray value-based correspondence probabilitiy (see next sub-Sect.). The product of the three is used to finally establish hard correspondences between feature points in fixed and moving image.5.3.3 Gray Value Descriptors
The ‘Robust Tree Registration’ approach by Loeckx et al. [25], mentioned in the previous section, uses the gray value-based ‘n-dimensional Scale-Invariant Feature Transform’ (n-SIFT) descriptor [8] in addition to a shape-based descriptor. The n-SIFT descriptor is an extension of the 2-dimensional SIFT descriptor introduced by Lowe [27]. The SIFT approach addresses feature localization as well as feature description. For feature localization, a resolution (scale) pyramid of Gaussian blurred images is created. ‘Difference-of-Gaussian’ (DoG) images are created by subtracting images of neighboring scales. Feature points are selected as local maxima (in space and scale) in the DoG images. The local orientation is determined based on a gradient orientation histogram around the feature point (see Fig. 5.2 for illustration). The described procedure delivers localization, orientation and scale of a feature point. The final feature description adds information about the local neighborhood of the feature point. First, the image gradient magnitudes and orientations are sampled around the feature point. To achieve orientation invariance, the gradient orientations are rotated relative to the feature point orientation. In order to avoid discontinuities of the descriptor for even small position changes and to give less emphasis to gradients that are far from the feature point, a Gaussian weighting function is used to assign a weight to the magnitude of each sample point. The weighted gradient magnitudes are collected block-wise in orientation histograms. The final descriptor is a vector containing the values of all the orientation histogram entries. In [25], the orientation histogram-based feature descriptor is taken instead of the DoG-based point selection to determine the correspondence between bifurcations in fixed and moving image. A cubic volume around each bifurcation is partitioned into 64 blocks and the gradient information is captured in a 60 bin histogram resulting in a 3840 dimensional feature vector. The feature descriptors are used in a probabilistic framework with the probability of correspondence between two bifurcations 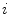 and
and 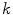 modeled as Gaussian function:
modeled as Gaussian function:
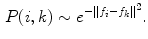
With 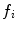 and
and 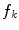 being the feature descriptor vector for bifurcation
being the feature descriptor vector for bifurcation 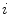 and
and 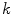 , and
, and 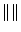 being the magnitude of the difference vector.
being the magnitude of the difference vector.
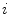 and
and 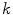 modeled as Gaussian function:
modeled as Gaussian function: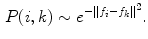
(5.3)
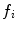 and
and 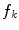 being the feature descriptor vector for bifurcation
being the feature descriptor vector for bifurcation 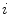 and
and 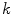 , and
, and 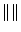 being the magnitude of the difference vector.
being the magnitude of the difference vector.
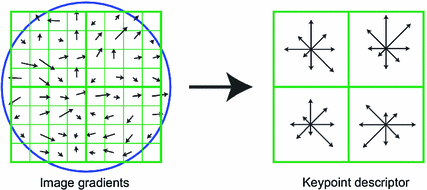
Fig. 5.2
Depiction of the gradient histogram based keypoint descriptor of the SIFT approach [27]. Image gradients (left) are weighted by a Gaussian window (blue circle) and are accumulated into orientation histograms summarizing the content of a subregion (right). The arrow length depicts the sum of the gradient magnitudes of the respective directional bin. The figure shows the case of a 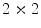 descriptor array computed from an
descriptor array computed from an 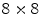 set of samples. Figure from Lowe [27]
set of samples. Figure from Lowe [27]
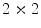 descriptor array computed from an
descriptor array computed from an 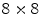 set of samples. Figure from Lowe [27]
set of samples. Figure from Lowe [27]The so-called SURF features, for ‘Speed-Up Robust Features’ [1] follow a similar line of thinking. In order to speed up the computation, SURF features are based on ‘Integral Images’ instead of a resolution pyramid of smoothed images. ‘Integral Images’ give for each pixel position the sum (integral) of image intensities of the image block spanned between image origin and pixel position. They allow the fast computation of approximated blurred derivatives using box-filters. Instead of local maxima of the DoG as in the case of SIFT, an approximated determinant of the Hessian matrix is used as detector of blob-like structures to localize feature points. The SURF descriptor captures information of the local neighborhood using first order Haar wavelets (see, e.g., [9]) responses, which again can be computed efficiently using the Integral Image. As in the SIFT case, image information is captured block wise around the feature point. Denoting the wavelet response in 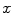 ,
, 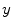 , and
, and 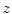 -direction with
-direction with 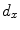 ,
, 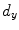 , and
, and 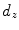 respectively, the feature descriptor for the ith block is given by the sum of responses within the block:
respectively, the feature descriptor for the ith block is given by the sum of responses within the block:
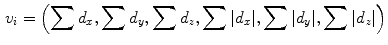 < div class='tao-gold-member'>
< div class='tao-gold-member'>




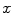 ,
, 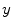 , and
, and 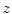 -direction with
-direction with 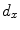 ,
, 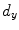 , and
, and 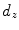 respectively, the feature descriptor for the ith block is given by the sum of responses within the block:
respectively, the feature descriptor for the ith block is given by the sum of responses within the block: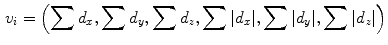
Only gold members can continue reading. Log In or Register to continue
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


