Chapter 8 Distribution of pulmonary ventilation and perfusion
 As a result of gravity, both ventilation and perfusion are distributed preferentially to dependent regions of the lung, and so vary with posture.
As a result of gravity, both ventilation and perfusion are distributed preferentially to dependent regions of the lung, and so vary with posture. In healthy lungs ventilation and perfusion are closely matched with little variation of the ventilation to perfusion (
In healthy lungs ventilation and perfusion are closely matched with little variation of the ventilation to perfusion (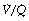 ) ratio in different lung regions.
) ratio in different lung regions. Regions of lung with
Regions of lung with 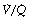 ratio of 0 represent intrapulmonary shunting of mixed venous blood, whilst regions with
ratio of 0 represent intrapulmonary shunting of mixed venous blood, whilst regions with 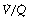 ratio of infinity constitute the alveolar dead space.
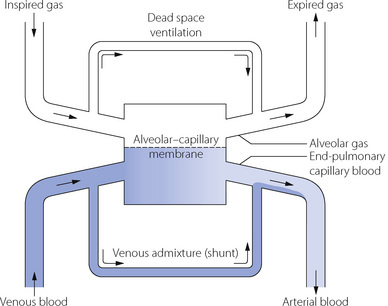
ratio of infinity constitute the alveolar dead space.The lung may be considered as a simple exchanger with a gas inflow and outflow, and a blood inflow and outflow (Figure 8.1). There is near-equilibrium of oxygen and carbon dioxide tensions between the two outflow streams from the exchanger itself. This theoretical model assumes that gas flow in and out of the alveolus and blood flow through the pulmonary capillary are both continuous. This assumption may be true within alveoli where at normal tidal volumes gas movement is by diffusion (page 19) but pulmonary capillary blood flow is pulsatile (page 101). This model has been deliberately drawn without countercurrent flow, which would be far more efficient. Such a system operates in the gills of fishes and the lungs of birds (page 289), and brings the Po2 of arterial blood close to the Po2 of their environment.
Distribution of Ventilation
Spatial and Anatomical Distribution of Inspired Gas
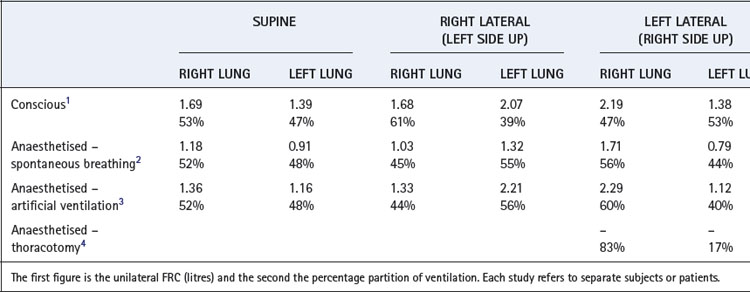
Distribution between the two lungs in the normal subject is influenced by posture and by the manner of ventilation. By virtue of its larger size, the right lung normally enjoys a ventilation slightly greater than the left lung in both the upright and the supine position (Table 8.1). In the lateral position, the lower lung is always better ventilated regardless of the side on which the subject is lying although there still remains a bias in favour of the right side.1 Fortunately, the preferential ventilation of the lower lung accords with increased perfusion of the same lung, so the ventilation/perfusion ratios of the two lungs are not greatly altered on assuming the lateral position. However, the upper lung tends to be better ventilated in the anaesthetised patient in the lateral position, regardless of the mode of ventilation and particularly with an open chest (Table 8.1).
In addition to causing postural differences between ventilation of the left and right lungs, gravity also influences the distribution of ventilation within each lung. Lung tissue may be considered as a semi-fluid or gel-like substance confined within the chest cavity, and the weight of the tissue above compresses the tissue below such that the density of the lung increases as vertical height reduces.5,6 Thus in dependent areas lung tissue is less expanded than in non-dependent areas and so is more compliant and receives more ventilation.
Distribution of ventilation to horizontal slices of lung has been studied for many years by inhalation of radioactive isotopes, this technique having the advantage of being easily performed in a variety of postures and the disadvantage of low spatial resolution. In the upright position, with slow vital capacity inspirations, uppermost slices of the lung have a ventilation of around one-third that of slices at the bases. A slow inspiration from functional residual capacity (FRC), as occurs during normal resting ventilation, results in a smaller vertical gradient down the lung with the ratio of basal to apical ventilation being approximately 1.5:1. In any horizontal position the vertical height of the lung is reduced by about 30% and therefore the gravitational force generating maldistribution is much less. A variety of scanning techniques can now be used to quantifying regional ventilation in the supine position,7,8,9 and have confirmed earlier findings that normal tidal breathing results in preferential ventilation of the posterior slices of the lungs compared with the anterior slices.10
Gravity is not the only factor influencing regional ventilation. Scanning techniques with the ability to measure ventilation in areas of lung only a few cubic millimetres in size have demonstrated increased ventilation in central, compared with peripheral, lung regions.5 This is likely to result from unequal branching patterns of the airways in a similar fashion to that seen in pulmonary blood vessels (see below).5
Distribution of Inspired Gas in Relation to the Rate of Alveolar Filling
The rate of inflation of the lung as a whole is a function of inflation pressure, compliance and airway resistance. It is convenient to think in terms of the time constant (explained in Appendix E), which is the product of the compliance and resistance and is:
 the time required for inflation to 63% of the final volume attained if inflation is prolonged indefinitely.
the time required for inflation to 63% of the final volume attained if inflation is prolonged indefinitely. the time that would be required for inflation of the lungs if the initial gas flow rate were maintained throughout inflation (see Appendix E, Figure E.6).
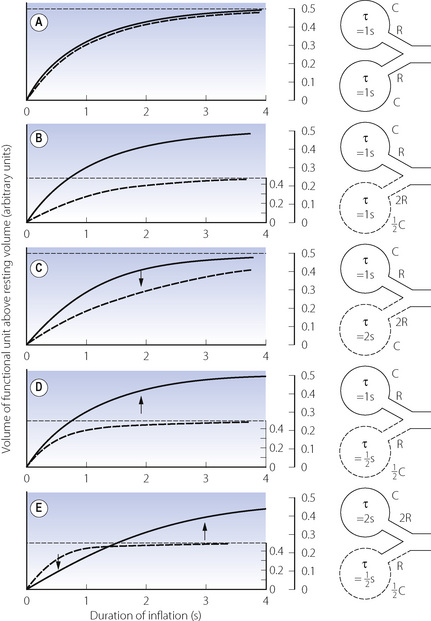
the time that would be required for inflation of the lungs if the initial gas flow rate were maintained throughout inflation (see Appendix E, Figure E.6).These considerations apply equally to large and small areas of the lungs; Figure 3.6 shows fast and slow alveoli, the former with a short time constant and the latter with a long time constant. Figure 8.2 shows some of the consequences of different functional units of the lung having different time constants. For simplicity, Figure 8.2 describes the response to passive inflation of the lungs by development of a constant mouth pressure but the considerations are fundamentally similar for both spontaneous respiration and artificial ventilation.
Figure 8.2A shows two functional units of identical compliance and resistance. If the mouth pressure is increased to a constant level, there will be an increase in volume of each unit equal to the mouth pressure multiplied by the compliance of the unit. The time course of inflation will follow the wash-in type of exponential function (Appendix E), and the time constants will be equal to the product of compliance and resistance of each unit and therefore identical. If the inspiratory phase is terminated at any instant, the pressure and volume of each unit will be identical and no redistribution of gas will occur between the two units.
Figure 8.2B shows two functional units, one of which has half the compliance but twice the resistance of the other. The time constants of the two will thus be equal. If a constant inflation pressure is maintained, the one with the lower compliance will increase in volume by half the volume change of the other. Nevertheless, the pressure build-up within each unit will be identical. Thus, as in the previous example, the relative distribution of gas between the two functional units will be independent of the rate or duration of inflation. If the inspiratory phase is terminated at any point, the pressure in each unit will be identical and no redistribution will occur between the different units.
In Figure 8.2C, the compliances of the two units are identical but the resistance of one is twice that of the other. Therefore, its time constant is double that of its fellow and it will fill more slowly, although the volume increase in both units will be the same if inflation is prolonged indefinitely. Relative distribution between the units is thus dependent on the rate and duration of inflation. If inspiration is checked by closure of the upper airway after 2 seconds (for example), the pressure will be higher in the unit with the lower resistance. Gas will then be redistributed from one unit to the other as shown by the arrow in the diagram.
Figure 8.2D shows a pair of units with identical resistances but the compliance of one being half that of the other. Its time constant is thus half that of its fellow and it has a faster time course of inflation. However, because its compliance is half that of the other, the ultimate volume increase will only be half that of the other unit when inflation is prolonged indefinitely. The relative distribution of gas between the two units is dependent upon the rate and duration of inflation. Pressure rises more rapidly in the unit with the lower compliance, and if inspiration is checked by closure of the upper airway at 2 seconds (for example), gas will be redistributed from one unit to the other as shown by the arrow.
An interesting and complex situation occurs when one unit has an increased resistance and the other a reduced compliance (Figure 8.2E). This combination also features in the presentation of the concept of fast and slow alveoli in Figure 3.6. In the present example the time constant of one unit is four times that of the other, while the ultimate volume changes are determined by the compliance as in Figure 8.2D. When the inflation pressure is sustained, the unit with the lower resistance (the ‘fast alveolus’) shows the greater volume change at first, but rapidly approaches its equilibrium volume. Thereafter the other unit (the ‘slow alveolus’) undergoes the major volume changes, the inflation of the two units being out of phase with one another. Throughout inspiration, the pressure build-up in the unit with the shorter time constant is always greater and, if inspiration is checked by closure of the upper airway, gas will be redistributed from one unit to the other as shown by the arrows in Figure 8.2E.
 Dynamic compliance (so far as it is influenced by considerations discussed in relation to Figure 3.7) will not be affected by changes in frequency and should not differ greatly from static compliance.
Dynamic compliance (so far as it is influenced by considerations discussed in relation to Figure 3.7) will not be affected by changes in frequency and should not differ greatly from static compliance. If inspiration is checked by closure of the upper airway, there will be no redistribution of gas within the lungs.
If inspiration is checked by closure of the upper airway, there will be no redistribution of gas within the lungs.If, however, the time constants of different units are different it follows that:
 Dynamic compliance will be decreased as respiratory frequency is increased and should differ significantly from static compliance.
Dynamic compliance will be decreased as respiratory frequency is increased and should differ significantly from static compliance.Effect of Maldistribution on the Alveolar ‘Plateau’
If different functional units of the lung empty synchronously during expiration, the composition of the expired air will be approximately constant after the gas in the airways (anatomical dead space) has been flushed out. However, this will not occur when there is maldistribution with fast and slow units as shown in Figure 3.7. The slow units are slow both to fill and to empty, and thus are hypoventilated for their volume; therefore they tend to have a high Pco2 and low Po2 and are slow to respond to a change in the inspired gas composition. This forms the basis of the single-breath test of maldistribution, in which a single breath of 100% oxygen is used to increase alveolar Po2 and decrease alveolar Pn2. The greatest increase of Po2 will clearly occur in the functional units with the best ventilation per unit volume, which will usually have the shortest time constants. The slow units will make the predominant contribution to the latter part of exhalation, when the mixed exhaled Po2 will decline and the Pn2 will increase. Thus the expired alveolar plateau of nitrogen will be sloping upwards in patients with maldistribution. It should, however, be stressed that this test will only be positive if maldistribution is accompanied by sequential emptying of units due to differing time constants. For example, Figure 8.2B shows definite maldistribution, due to the different regional compliances that directly influence the regional ventilation. However, because time constants are equal, there will be a constant mix of gas from both units during the course of expiration (i.e. no sequential emptying) and therefore the alveolar plateau would remain flat in spite of Po2 and Pn2 being different for the two units. However, maldistribution due to the commoner forms of lung disease is usually associated with different time constants and sequential emptying. Routine continuous monitoring of expired carbon dioxide concentration during anaesthesia allows some assessment of maldistribution of ventilation. As for the single breath nitrogen test, an upward sloping expiratory plateau of carbon dioxide indicates sequential emptying of alveoli with different time constants (page 175), but a level plateau does not indicate normal distribution of ventilation, just equal time constants of lung units.
Distribution of Perfusion
Distribution between the two lungs. Measuring unilateral pulmonary blood flow in humans is difficult, but indirect methods show that unilateral pulmonary blood flow is similar to the distribution of ventilation observed in the supine position (Table 8.1). In the lateral position, the diameter of the thorax is of the order of 30 cm and so the column of blood in the pulmonary circulation exerts a hydrostatic pressure that is high in relation to the mean pulmonary arterial pressure. A fairly gross maldistribution therefore occurs with much of the upper lung comprising zone 2 and much of the lower lung comprising zone 3 (see Figure 7.5).11
Gravitational Effects on Regional Pulmonary Blood Flow
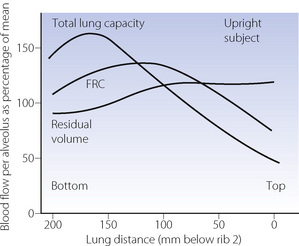
In the previous chapter, it was shown how the pulmonary vascular resistance is mainly in the capillary bed and is governed by the relationship between alveolar, pulmonary arterial and pulmonary venous pressures. Early studies with radioactive tracers in the blood took place at total lung capacity and showed flow increasing progressively down the lung in the upright position. However, Hughes et al. later found that there was a significant reduction of flow in the most dependent parts of the lung, which was termed zone 4, where the reduction in flow appears to be due to compression of larger blood vessels by increased interstitial pressure.12 This effect becomes progressively more important as lung volume was reduced from total lung capacity towards the residual volume. Figure 8.3 is derived from the work of Hughes’ group, and shows that pulmonary perfusion per alveolus is, in fact, reasonably uniform at the lung volumes relevant to normal tidal exchange. However, the dependent parts of the lung contain larger numbers of smaller alveoli than the apices at FRC, and the perfusion per unit lung volume is therefore increased at the bases.11
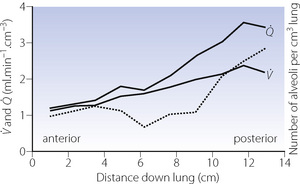
In the supine position the differences in blood flow between apices and bases are replaced by differences between anterior and posterior regions. Supine subjects can be studied using the same variety of scanning techniques as used for assessing ventilation (page 138), revealing the same height-dependent gradients in alveolar size and perfusion as seen in earlier observations in upright subjects. Blood flow per unit lung volume increases by 11% per cm of descent through the lung,13 whilst ventilation increases but less dramatically (Figure 8.4),14 resulting in a smaller ventilation to perfusion ratio in dependent areas.13 These studies also showed that the number of alveoli per cubic centimetre of lung was approximately 30% greater in the posterior compared with anterior lung (Figure 8.4).14 Thus the increased perfusion in dependent areas of lung is again mainly caused by an increase in the number of (relatively small) alveoli. Smaller more numerous alveoli in dependent regions result from the weight of lung tissue above, and as blood accounts for two thirds of the weight of lung tissue this provides an automatic matching of ventilation and perfusion.
Gravity-Independent Regional Blood Flow5
It is now accepted that gravity is not the only cause of the variability of regional pulmonary blood flow, though its relative contribution remains controversial.15,16 Physiological studies in space some years ago showed that at microgravity regional blood flow becomes more uniform than on Earth, but residual non-uniformity still persists (page 308). A variety of methods have been used to study pulmonary blood flow in the prone position.13,14,17 These studies have consistently found that although blood flow becomes more uniform, the flow distribution when prone is not simply a reversal of the supine position, as may be expected if gravity was the only influence.18
Some groups estimate that gravity is responsible for only 25% of the regional blood flow variability seen.5,17 Pulmonary blood flow may vary in a radial fashion, with greater flow to central, compared to peripheral, lung regions in each horizontal slice of lung.19 Regional flow is believed to be influenced by vascular architecture, with the branching pattern of the pulmonary vasculature being responsible for the observed gravity-independent variation (the fractal hypothesis).20 Two aspects of vascular structure contribute to the variations in flow. First, bifurcations of pulmonary arteries into two slightly different size vessels will have a large effect on the flow rates in each.5 Secondly, pulmonary arteries are more numerous than pulmonary airways as a result of small extra branches, often given off at right angles, throughout the pulmonary arterial tree. Mathematical modelling indicates that these ‘supernumerary’ branches contribute significantly to the heterogeneity of regional perfusion.21
Ventilation in Relation to Perfusion22
Alveoli with no ventilation (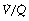 ratio of zero) will have Po2 and Pco2 values that are the same as those of mixed venous blood, because the trapped air in the unventilated alveoli will equilibrate with mixed venous blood. Alveoli with no perfusion (
ratio of zero) will have Po2 and Pco2 values that are the same as those of mixed venous blood, because the trapped air in the unventilated alveoli will equilibrate with mixed venous blood. Alveoli with no perfusion (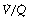 ratio of infinity) will have Po2 and Pco2 values that are the same as those of the inspired gas, because there is no gas exchange to alter the composition of the inspired gas that is drawn into these alveoli. Alveoli with intermediate values of
ratio of infinity) will have Po2 and Pco2 values that are the same as those of the inspired gas, because there is no gas exchange to alter the composition of the inspired gas that is drawn into these alveoli. Alveoli with intermediate values of 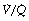 ratio will thus have Po2 and Pco2 values that are intermediate between those of mixed venous blood and inspired gas. Figure 8.5 is a Po2/Pco2 plot with the thick line joining the mixed venous point to the inspired gas point. This line covers all possible combinations of alveolar Po2 and Pco2, with an indication of the
ratio will thus have Po2 and Pco2 values that are intermediate between those of mixed venous blood and inspired gas. Figure 8.5 is a Po2/Pco2 plot with the thick line joining the mixed venous point to the inspired gas point. This line covers all possible combinations of alveolar Po2 and Pco2, with an indication of the 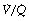 ratios that determine them.
ratios that determine them.
The inhalation of higher than normal partial pressures of oxygen moves the inspired point of the curve to the right. The mixed venous point also moves to the right but only by a small amount for reasons that are explained on page 377. A new curve must be prepared for each combination of values for mixed venous blood and inspired gas. The curve can then be used to demonstrate the gas tensions in the horizontal strata of the lung according to their different 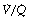 ratios (Figure 8.5).
ratios (Figure 8.5).
All of the techniques described above that measure regional ventilation and perfusion in horizontal strata of the lung only discriminate between functionally large regions of the lung. This limitation was overcome by the multiple inert gas elimination technique (MIGET).23 The methodology, which is outlined on page 138, permits the plotting of the distribution of pulmonary ventilation and perfusion, not in relation to anatomical location, but in a large number of compartments defined by their 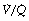 ratios, expressed on a logarithmic scale.
ratios, expressed on a logarithmic scale.
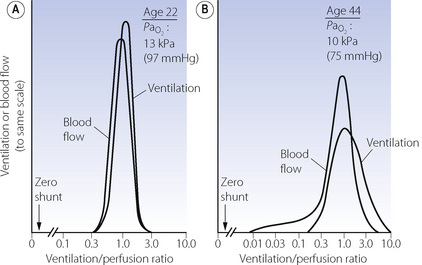
Figure 8.6 shows typical plots for healthy subjects.24 For the young adult (Figure 8.6A), both ventilation and perfusion are mainly confined to alveoli with 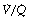 ratios in the range 0.5–2.0. There is no measurable distribution to areas of infinite
ratios in the range 0.5–2.0. There is no measurable distribution to areas of infinite 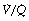 (i.e. alveolar dead space) or zero
(i.e. alveolar dead space) or zero 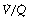 ratio (i.e. intrapulmonary shunt), but the method does not detect extrapulmonary shunt which must be present to a small extent (page 132). For the older subject (Figure 8.6B), there is a widening of the distribution of
ratio (i.e. intrapulmonary shunt), but the method does not detect extrapulmonary shunt which must be present to a small extent (page 132). For the older subject (Figure 8.6B), there is a widening of the distribution of 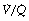 ratios, with the main part of the curve now in the range of
ratios, with the main part of the curve now in the range of 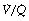 ratios 0.3–5.0. In addition, there is the appearance of a ‘shelf’ of distribution of blood flow to areas of low
ratios 0.3–5.0. In addition, there is the appearance of a ‘shelf’ of distribution of blood flow to areas of low 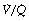 ratio in the range 0.01–0.3. This probably represents gross underventilation of dependent areas of the lung due to airway closure when the closing capacity exceeds the functional residual capacity (see Figure 3.11). The effect of increased spread of
ratio in the range 0.01–0.3. This probably represents gross underventilation of dependent areas of the lung due to airway closure when the closing capacity exceeds the functional residual capacity (see Figure 3.11). The effect of increased spread of 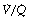 ratios on gas exchange is considered below (page 136).
ratios on gas exchange is considered below (page 136).
(After reference 24 by permission of the authors and copyright permission of the American Society for Clinical Investigation.)
The pattern of distribution of  ratios shows characteristic changes in a number of pathological conditions such as pulmonary oedema and pulmonary embolus.25 Some examples are shown in Figure 8.7.
ratios shows characteristic changes in a number of pathological conditions such as pulmonary oedema and pulmonary embolus.25 Some examples are shown in Figure 8.7.
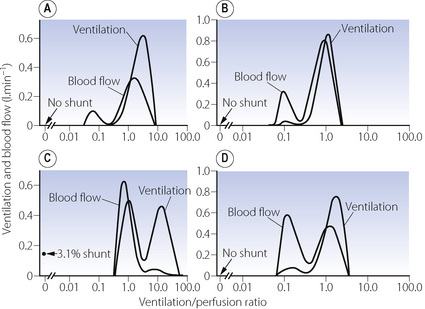
Fig. 8.7 Examples of abnormal patterns of maldistribution of ventilation and perfusion, to be compared with the normal curves in Figure 8.6. (A) Chronic obstructive pulmonary disease. The blood flow to units of very low  ratio would cause arterial hypoxaemia and simulate a shunt. (B) Asthma, with a more pronounced bimodal distribution of blood flow than the patient shown in (A). (C) Bimodal distribution of ventilation in a 60-year-old patient with chronic obstructive pulmonary disease, predominantly emphysema. A similar pattern is seen after pulmonary embolism. (D) Pronounced bimodal distribution of perfusion after a bronchodilator was administered to the patient shown in (B).
ratio would cause arterial hypoxaemia and simulate a shunt. (B) Asthma, with a more pronounced bimodal distribution of blood flow than the patient shown in (A). (C) Bimodal distribution of ventilation in a 60-year-old patient with chronic obstructive pulmonary disease, predominantly emphysema. A similar pattern is seen after pulmonary embolism. (D) Pronounced bimodal distribution of perfusion after a bronchodilator was administered to the patient shown in (B).
(After reference 25 by permission of the author and publishers.)
Quantification of Spread of 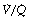 Ratios as if it were due to Dead Space and Shunt
Ratios as if it were due to Dead Space and Shunt
The MIGET method of analysis illustrated in Figures 8.6 and 8.7 is technically complex. A less precise but highly practical approach was described in the 1940s by both Fenn et al26 and Riley & Cournard.27 The essence of what has generally become known as the Riley approach is to consider the lung as if it were a three-compartment model (Figure 8.8) comprising:
Gas exchange can only occur in the ‘ideal’ alveolus. There is no suggestion that this is an accurate description of the actual state of affairs, which is better depicted by the type of plot shown in Figure 8.6, where the analysis would comprise some 50 compartments in contrast to the three compartments of the Riley model. However, the parameters of the three-compartment model may be easily determined and the values obtained are of direct relevance to therapy. Thus an increased dead space can usually be offset by an increased minute volume, and arterial Po2 can be restored to normal with shunts up to about 30% by an appropriate increase in the inspired oxygen concentration (see Figure 8.11 below).
Methods for calculating dead space and shunt for the three-compartment model are described at the end of the chapter, but no analytical techniques are required beyond measurement of blood and gas Pco2 and Po2. It is then possible to determine what fraction of the inspired tidal volume does not participate in gas exchange and what fraction of the cardiac output constitutes a shunt. However, it is most important to remember that the measured value for ‘dead space’ will include a fraction representing ventilation of relatively underperfused alveoli, and the measured value for ‘shunt’ will include a fraction representing perfusion of relatively underventilated alveoli. Furthermore, although perfusion of relatively underventilated alveoli will reduce arterial Po2, the pattern of change, in relation to the inspired oxygen concentration, is quite different from that of a true shunt (see Figure 8.12 below).
The concept of ‘ideal’ alveolar gas is considered below (page 139), but it will be clear from Figure 8.8 that ideal alveolar gas cannot be sampled for analysis. There is a convention that ideal alveolar Pco2 is assumed to be equal to the arterial Pco2 and that the respiratory exchange ratio of ideal alveolar gas is the same as that of expired air.




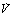 ) and perfusion (
) and perfusion (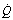 ) per cubic centimetre of lung tissue. Ventilation and perfusion both increase on descending through the lung. The dotted line relates to the right ordinate and represents the number of alveoli per unit lung volume, which increases in dependent areas such that the blood flow per alveolus remains fairly constant.
) per cubic centimetre of lung tissue. Ventilation and perfusion both increase on descending through the lung. The dotted line relates to the right ordinate and represents the number of alveoli per unit lung volume, which increases in dependent areas such that the blood flow per alveolus remains fairly constant.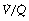 ). Each quantity is measured in litres per minute and taking the lungs as a whole, typical resting values might be 4 l.min−1 for alveolar ventilation and 5 l.min−1 for pulmonary blood flow. Thus the overall ventilation perfusion ratio would be 0.8. If ventilation and perfusion of all alveoli were uniform then each alveolus would have an individual
). Each quantity is measured in litres per minute and taking the lungs as a whole, typical resting values might be 4 l.min−1 for alveolar ventilation and 5 l.min−1 for pulmonary blood flow. Thus the overall ventilation perfusion ratio would be 0.8. If ventilation and perfusion of all alveoli were uniform then each alveolus would have an individual 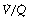 ratio of 0.8. In fact, ventilation and perfusion are not uniformly distributed but may range all the way from unventilated alveoli to unperfused alveoli with every gradation in between. Unventilated alveoli will have a
ratio of 0.8. In fact, ventilation and perfusion are not uniformly distributed but may range all the way from unventilated alveoli to unperfused alveoli with every gradation in between. Unventilated alveoli will have a 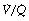 ratio of zero and the unperfused alveoli a
ratio of zero and the unperfused alveoli a 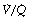 ratio of infinity.
ratio of infinity.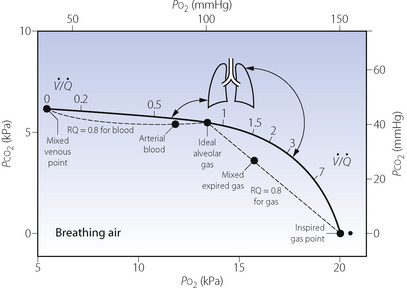
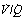 ) ratios ranging from zero to infinity (subject breathing air). Values for normal alveoli are distributed as shown in accord with their vertical distance up the lung field. Mixed expired gas may be considered as a mixture of ‘ideal’ alveolar and inspired gas (dead space). Arterial blood may be considered as a mixture of blood with the same gas tensions as ‘ideal’ alveolar gas and mixed venous blood (shunt).
) ratios ranging from zero to infinity (subject breathing air). Values for normal alveoli are distributed as shown in accord with their vertical distance up the lung field. Mixed expired gas may be considered as a mixture of ‘ideal’ alveolar and inspired gas (dead space). Arterial blood may be considered as a mixture of blood with the same gas tensions as ‘ideal’ alveolar gas and mixed venous blood (shunt).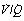 ) ratios in two normal subjects. (A) A male aged 22 years with typical narrow spread and no measurable intrapulmonary shunt or alveolar dead space. (B) The wider spread of
) ratios in two normal subjects. (A) A male aged 22 years with typical narrow spread and no measurable intrapulmonary shunt or alveolar dead space. (B) The wider spread of 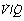 ratios in a male aged 44 years. There is still no measurable intrapulmonary shunt or alveolar dead space, but the appreciable distribution of blood flow to underperfused alveoli is sufficient to reduce the arterial P
ratios in a male aged 44 years. There is still no measurable intrapulmonary shunt or alveolar dead space, but the appreciable distribution of blood flow to underperfused alveoli is sufficient to reduce the arterial P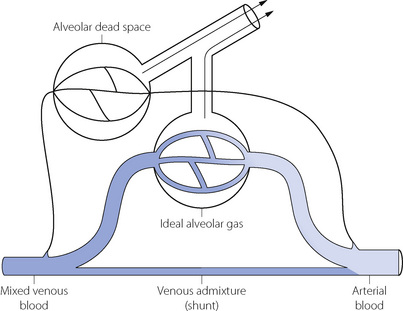
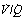 scatter. The measured venous admixture consists of true venous admixture (shunt) together with a component caused by
scatter. The measured venous admixture consists of true venous admixture (shunt) together with a component caused by 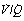 scatter. Note that ‘ideal’ alveolar gas is exhaled contaminated with alveolar dead space gas, so it is not possible to sample ‘ideal’ alveolar gas.
scatter. Note that ‘ideal’ alveolar gas is exhaled contaminated with alveolar dead space gas, so it is not possible to sample ‘ideal’ alveolar gas.


