.
Relative to the electric-field induced depolarization next to a straight boundary, electrotonic effects lead to an enhancement of the maximum tissue depolarization towards negative curvatures and a decline towards positive curvatures. This is qualitatively in line with a series of cell culture experiments revealing an increased sensitivity of negative-curvature boundaries. Theoretically, the relevant quantity determining the strength of this curvature effect in the vicinity of curvature zero was determined to be the normalized mean curvature 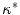 (in both two and three dimensions). In the natural, normalized units of the problem, this difference to the depolarization of a straight boundary was shown to be just
(in both two and three dimensions). In the natural, normalized units of the problem, this difference to the depolarization of a straight boundary was shown to be just 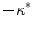 . For larger deviations from a straight boundary, the global shape of the tissue becomes important: while for parabolic boundaries or protrusions, the maximum depolarization caused by an electric field is monotonic in the curvature, there is a maximum effect strength for a specific value of (negative) curvature for circular boundaries, caused by the interaction of the “pure” curvature effect and the spatial vicinity of depolarized and hyperpolarized boundaries. For small tissue domains of arbitrary shape (on a length scale much shorter than
. For larger deviations from a straight boundary, the global shape of the tissue becomes important: while for parabolic boundaries or protrusions, the maximum depolarization caused by an electric field is monotonic in the curvature, there is a maximum effect strength for a specific value of (negative) curvature for circular boundaries, caused by the interaction of the “pure” curvature effect and the spatial vicinity of depolarized and hyperpolarized boundaries. For small tissue domains of arbitrary shape (on a length scale much shorter than 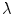 ), this interaction was shown to result in a maximum depolarization proportional to the length of the domain in the direction of the electric field. An analytical argument was presented which makes it possible to transfer the results for one- or two-dimensional tissue domains to higher dimensions.
), this interaction was shown to result in a maximum depolarization proportional to the length of the domain in the direction of the electric field. An analytical argument was presented which makes it possible to transfer the results for one- or two-dimensional tissue domains to higher dimensions.
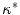 (in both two and three dimensions). In the natural, normalized units of the problem, this difference to the depolarization of a straight boundary was shown to be just
(in both two and three dimensions). In the natural, normalized units of the problem, this difference to the depolarization of a straight boundary was shown to be just 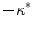 . For larger deviations from a straight boundary, the global shape of the tissue becomes important: while for parabolic boundaries or protrusions, the maximum depolarization caused by an electric field is monotonic in the curvature, there is a maximum effect strength for a specific value of (negative) curvature for circular boundaries, caused by the interaction of the “pure” curvature effect and the spatial vicinity of depolarized and hyperpolarized boundaries. For small tissue domains of arbitrary shape (on a length scale much shorter than
. For larger deviations from a straight boundary, the global shape of the tissue becomes important: while for parabolic boundaries or protrusions, the maximum depolarization caused by an electric field is monotonic in the curvature, there is a maximum effect strength for a specific value of (negative) curvature for circular boundaries, caused by the interaction of the “pure” curvature effect and the spatial vicinity of depolarized and hyperpolarized boundaries. For small tissue domains of arbitrary shape (on a length scale much shorter than 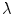 ), this interaction was shown to result in a maximum depolarization proportional to the length of the domain in the direction of the electric field. An analytical argument was presented which makes it possible to transfer the results for one- or two-dimensional tissue domains to higher dimensions.
), this interaction was shown to result in a maximum depolarization proportional to the length of the domain in the direction of the electric field. An analytical argument was presented which makes it possible to transfer the results for one- or two-dimensional tissue domains to higher dimensions.In numerical simulations based on the Fenton-Karma model, two restrictions of the theory (infinitesimal field strengths and infinite pulse duration) were determined not to be essential for its applicability to realistic scenarios of electric-field stimulation of cardiac tissue with a complex geometry. Qualitatively, the higher sensitivity of negative-curvature boundaries, and therefore its response to lower electric fields, could be confirmed in those simulations.
In a systematic study for circular boundaries, it was shown that there are quantitative differences in the field strength necessary for wave induction, which, for an experimentally relevant pulse duration, depend on the pulse shape. However, the existence of an optimal radius for circular tissue regions was found, though for slightly different values of the curvature, to be independent of the pulse shape. The differences in critical field strength between different stimulation wave forms could be explained with a shape-dependent time scale for the electric-field induced depolarization next to a tissue boundary. This time scale was found to be in agreement with the time scale on which the membrane potential approaches the steady-state solution in the low field strength approximation. Broadly speaking, high-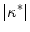 boundaries were found to depolarize on smaller time scales, leading to only small differences in the critical field strength between biphasic and monophasic pulses. At the same time, the short time scales result in an advantage of truncated exponential wave forms in terms of the average field strength necessary for wave induction, because the effect of the initial high field strength implied by the wave form is more pronounced. In contrast, longer time scales for small-
boundaries were found to depolarize on smaller time scales, leading to only small differences in the critical field strength between biphasic and monophasic pulses. At the same time, the short time scales result in an advantage of truncated exponential wave forms in terms of the average field strength necessary for wave induction, because the effect of the initial high field strength implied by the wave form is more pronounced. In contrast, longer time scales for small-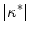 boundaries lead to a larger difference between biphasic and monophasic pulses, while simultaneously canceling out the advantageous effect of the exponential wave form.
boundaries lead to a larger difference between biphasic and monophasic pulses, while simultaneously canceling out the advantageous effect of the exponential wave form.
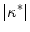 boundaries were found to depolarize on smaller time scales, leading to only small differences in the critical field strength between biphasic and monophasic pulses. At the same time, the short time scales result in an advantage of truncated exponential wave forms in terms of the average field strength necessary for wave induction, because the effect of the initial high field strength implied by the wave form is more pronounced. In contrast, longer time scales for small-
boundaries were found to depolarize on smaller time scales, leading to only small differences in the critical field strength between biphasic and monophasic pulses. At the same time, the short time scales result in an advantage of truncated exponential wave forms in terms of the average field strength necessary for wave induction, because the effect of the initial high field strength implied by the wave form is more pronounced. In contrast, longer time scales for small-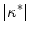 boundaries lead to a larger difference between biphasic and monophasic pulses, while simultaneously canceling out the advantageous effect of the exponential wave form.
boundaries lead to a larger difference between biphasic and monophasic pulses, while simultaneously canceling out the advantageous effect of the exponential wave form.In the experimental investigation presented in Sect. 3.3, the recruitment mechanism for intramural wave sources underlying LEAP was studied. The hypothesis was that the cardiovascular tree provides the heterogeneities in conductance giving rise to multiple pacing sites for LEAP, which act as control sites for spatio-temporal chaos during fibrillation. To test this hypothesis, isolated cardiac tissue preparations of canine atria and ventricles were artificially perfused and observed in-vitro using the technique of optical voltage mapping.
The theoretical wave source density was calculated from size distributions of the coronary vessels, which were obtained from 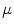 CT scans of the tissue preparations perfused with contrast agent. Based on the size statistics, in accordance with the results of Sect. 3.2, the asymptotic theory for circular heterogeneities developed by Pumir and Krinsky [2] was utilized to theoretically determine the fraction of (cylindrical) blood vessels activated at a certain electric field strength. A simplistic model was constructed connecting a specific wave source density in the bulk of the cardiac muscle to an observed activation time. In the in-vitro experiments, this proxy quantity was directly measured following the stimulation of quiescent tissue with short electric-field pulses.
CT scans of the tissue preparations perfused with contrast agent. Based on the size statistics, in accordance with the results of Sect. 3.2, the asymptotic theory for circular heterogeneities developed by Pumir and Krinsky [2] was utilized to theoretically determine the fraction of (cylindrical) blood vessels activated at a certain electric field strength. A simplistic model was constructed connecting a specific wave source density in the bulk of the cardiac muscle to an observed activation time. In the in-vitro experiments, this proxy quantity was directly measured following the stimulation of quiescent tissue with short electric-field pulses.
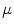 CT scans of the tissue preparations perfused with contrast agent. Based on the size statistics, in accordance with the results of Sect. 3.2, the asymptotic theory for circular heterogeneities developed by Pumir and Krinsky [2] was utilized to theoretically determine the fraction of (cylindrical) blood vessels activated at a certain electric field strength. A simplistic model was constructed connecting a specific wave source density in the bulk of the cardiac muscle to an observed activation time. In the in-vitro experiments, this proxy quantity was directly measured following the stimulation of quiescent tissue with short electric-field pulses.
CT scans of the tissue preparations perfused with contrast agent. Based on the size statistics, in accordance with the results of Sect. 3.2, the asymptotic theory for circular heterogeneities developed by Pumir and Krinsky [2] was utilized to theoretically determine the fraction of (cylindrical) blood vessels activated at a certain electric field strength. A simplistic model was constructed connecting a specific wave source density in the bulk of the cardiac muscle to an observed activation time. In the in-vitro experiments, this proxy quantity was directly measured following the stimulation of quiescent tissue with short electric-field pulses.Both the size distributions and the activation times as a function of the field strength were found to follow power laws, whose exponents could be connected analytically to each other, separately for atria and ventricles, with good quantitative agreement. Even better consistency could be reached by using the above model to predict activation times directly from the measured size distributions. The inverse relationship was used to construct hypothetical size distributions of circular heterogeneities which could be responsible for the observed activation times. Again, good quantitative agreement with the real size distributions of the cardiovasculature was found. These results [4] provide a strong empirical basis for the relevance of the cardiovascular tree as wave nucleation sites during LEAP in the considered field strength range.
Using the same experimental technique, but an improved and computer-controlled protocol, activation times were also measured in perfused ventricular preparations of pig hearts. Although size distributions of the coronary vessels were not available yet, the optical mapping experiments indicate that the power law behavior of the activation times is a universal feature across species and different pulse shapes, which suggests that LEAP efficacy should not depend fundamentally upon species or the technical implementation details of the defibrillator. Quantitatively, it was found that for pulse durations of 10 ms, the total injected current alone (or, equivalently, the mean electric field strength) determines the density of recruited wave sources, independent of the pulse shape.
4.2 Discussion and Outlook
The aim of Sect. 3.1 was to establish Lyapunov stability analysis as a new tool for the characterization of the dynamics in models of cardiac tissue or, more generally, excitable media. As outlined in the introduction, the study of the stability of activation patterns is an attempt to conceptually understand how undesired spatio-temporal activation patterns arise and to quantify the complexity of such dynamics. The work presented in the first subsections of Sect. 3.1 can be viewed as a methodological proof of principle in this context. It shows that the acquisition of Lyapunov spectra in numerical models of excitable media with a vast number of degrees of freedom is feasible and leads to meaningful results despite the infinite-dimensional phase space of the underlying PDE. Its main advantage over the linear stability analysis of fixed points is that it can be applied to arbitrary trajectories and does not require any considerable algorithmic effort. Although the computational demand increases with the number of perturbation modes integrated along with the system dynamics, by construction, reaction-diffusion systems are easily linearized, as the Jacobian of the (relatively low-dimensional) local dynamics can usually be calculated analytically, and diffusion acts in the same way as in the original system.
To systematically gain an understanding of the meaning of Lyapunov spectra for these systems, relatively simple scenarios in the Barkley and (smooth) Fenton-Karma model were considered in the beginning of Sect. 3.1, in particular to make the transition from existing results of the linear stability analysis of fixed points [5–7] and response functions [8, 9]. Future studies could be extended to other models of cardiac tissue, including spiral waves with non-circular cores and instabilities leading to breakup [10]. Moreover, deviations from the scenario of multiple independent spiral waves presented in Sect. 3.1.3 could reveal valuable information on the mechanisms governing the interaction between spiral waves in more realistic models of cardiac tissue. These could turn out to be important for strategies aiming at the termination of individual spiral waves, depending on whether they can be viewed as independent waves or have to be considered “entangled” in some way.
From a methodological point of view, one important aspect of the method is that destabilizing effects can already be detected before the modes actually become unstable, something that would not be possible by simply observing the dynamics: For example, in Fig. 3.12 (p. 103), for stable spiral waves, the rate with which the meandering modes are destabilized indicates, whether there is a danger of arriving at a bifurcation (in this case, the nature of the bifurcation could even be identified from the spatial structure of the corresponding Lyapunov vectors). Similarly, during spatio-temporal chaos, the subtle stabilizing effect of heterogeneities in excitability was already detectable via the Lyapunov dimension for small heterogeneities, but visible effects like spiral wave pinning or reduced number fluctuations of phase singularities were only observed for specific sizes of heterogeneities (cf. Fig. 3.19, p. 113). In the future, this predictive power of Lyapunov stability analysis could help to identify the critical directions in the usually large parameter space of detailed, physiological, cardiac models which make the dynamics more vulnerable to instabilities. Similarly, it could facilitate the search for possible countermeasures suppressing a developing instability or reducing the complexity of a turbulent state.
The results on the influence of heterogeneities presented in Sects. 3.1.5, 3.1.6 and 3.1.7 point to a whole new class of interesting but difficult questions regarding the proarrhythmic or antiarrhythmic effect of local changes in the properties of cardiac tissue. Similar to the effect of increased 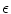 in the Bär-Eiswirth model (in a homogeneous medium), it is a generally accepted fact that reduced excitability in cardiac tissue is proarrhythmic [11]. The results presented here suggest that it is, in general, not possible to predict the effect of a local parameter change from a known behavior in a homogeneous medium. Thus, if excitability is reduced in a spatially heterogeneous manner in the heart, the effects might differ greatly from those observed for global changes of physiological conditions or expected on the basis of mean tissue properties. Furthermore, the results show that the effects could depend in a non-trivial manner on the length scale and the strength of the heterogeneity. As meandering for a single spiral wave was only observed for the step-wise heterogeneity considered in Sect. 3.1.5 but not for the random, smooth heterogeneities imposed in Sect. 3.1.6, the steepness in the change of properties towards the heterogeneous region apparently is another determining factor. Heterogeneity-induced complexity changes during spiral wave or chaotic activity could be of particular relevance for the termination of tachycardia or fibrillation in diseased hearts, when the natural heterogeneity is increased, either facilitating or impeding low-energy termination efforts. An investigation of such effects should be carried out by simultaneously considering the results of Sect. 3.3 and the effect the additional heterogeneity might have on wave source recruitment during electric-field stimulation.
in the Bär-Eiswirth model (in a homogeneous medium), it is a generally accepted fact that reduced excitability in cardiac tissue is proarrhythmic [11]. The results presented here suggest that it is, in general, not possible to predict the effect of a local parameter change from a known behavior in a homogeneous medium. Thus, if excitability is reduced in a spatially heterogeneous manner in the heart, the effects might differ greatly from those observed for global changes of physiological conditions or expected on the basis of mean tissue properties. Furthermore, the results show that the effects could depend in a non-trivial manner on the length scale and the strength of the heterogeneity. As meandering for a single spiral wave was only observed for the step-wise heterogeneity considered in Sect. 3.1.5 but not for the random, smooth heterogeneities imposed in Sect. 3.1.6, the steepness in the change of properties towards the heterogeneous region apparently is another determining factor. Heterogeneity-induced complexity changes during spiral wave or chaotic activity could be of particular relevance for the termination of tachycardia or fibrillation in diseased hearts, when the natural heterogeneity is increased, either facilitating or impeding low-energy termination efforts. An investigation of such effects should be carried out by simultaneously considering the results of Sect. 3.3 and the effect the additional heterogeneity might have on wave source recruitment during electric-field stimulation.
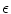 in the Bär-Eiswirth model (in a homogeneous medium), it is a generally accepted fact that reduced excitability in cardiac tissue is proarrhythmic [11]. The results presented here suggest that it is, in general, not possible to predict the effect of a local parameter change from a known behavior in a homogeneous medium. Thus, if excitability is reduced in a spatially heterogeneous manner in the heart, the effects might differ greatly from those observed for global changes of physiological conditions or expected on the basis of mean tissue properties. Furthermore, the results show that the effects could depend in a non-trivial manner on the length scale and the strength of the heterogeneity. As meandering for a single spiral wave was only observed for the step-wise heterogeneity considered in Sect. 3.1.5 but not for the random, smooth heterogeneities imposed in Sect. 3.1.6, the steepness in the change of properties towards the heterogeneous region apparently is another determining factor. Heterogeneity-induced complexity changes during spiral wave or chaotic activity could be of particular relevance for the termination of tachycardia or fibrillation in diseased hearts, when the natural heterogeneity is increased, either facilitating or impeding low-energy termination efforts. An investigation of such effects should be carried out by simultaneously considering the results of Sect. 3.3 and the effect the additional heterogeneity might have on wave source recruitment during electric-field stimulation.
in the Bär-Eiswirth model (in a homogeneous medium), it is a generally accepted fact that reduced excitability in cardiac tissue is proarrhythmic [11]. The results presented here suggest that it is, in general, not possible to predict the effect of a local parameter change from a known behavior in a homogeneous medium. Thus, if excitability is reduced in a spatially heterogeneous manner in the heart, the effects might differ greatly from those observed for global changes of physiological conditions or expected on the basis of mean tissue properties. Furthermore, the results show that the effects could depend in a non-trivial manner on the length scale and the strength of the heterogeneity. As meandering for a single spiral wave was only observed for the step-wise heterogeneity considered in Sect. 3.1.5 but not for the random, smooth heterogeneities imposed in Sect. 3.1.6, the steepness in the change of properties towards the heterogeneous region apparently is another determining factor. Heterogeneity-induced complexity changes during spiral wave or chaotic activity could be of particular relevance for the termination of tachycardia or fibrillation in diseased hearts, when the natural heterogeneity is increased, either facilitating or impeding low-energy termination efforts. An investigation of such effects should be carried out by simultaneously considering the results of Sect. 3.3 and the effect the additional heterogeneity might have on wave source recruitment during electric-field stimulation.One should bear in mind that spiral waves in the ventricles are organized around three-dimensional filaments that evolve in a medium of irregular shape, which adds considerable complexity to the problem. However, following the mathematical line of thoughts outlined in Sect. 2.2.6, it should in principle be possible to apply Lyapunov stability analysis to numerical simulations of cardiac activity on realistic geometries. In this way, the complexity of fibrillation and its influence on controllability by low-energy methods could be tested in a realistic scenario. Another possible application of Lyapunov analysis for realistic simulations could be based on the analogy of plane waves to the synchronization of coupled oscillators: The creation of a reentry pattern underlying tachycardia requires the break of the plane wave. This process could be viewed as a destabilization of synchronization between pathways in the heart which, under normal conditions, are activated in parallel. In view of the recent popularity of covariant Lyapunov vectors, another possible application of Lyapunov stability analysis is during spatio-temporal chaos. While in Sect. 3.1, most of the Lyapunov vectors (except for the meandering modes) were located in the degenerated subspace of the largest Lyapunov exponent, which is automatically covariant, general covariant Lyapunov vectors have been shown to allow for an independent definition of an effective physical dimension in other extended systems exhibiting spatio-temporal chaos [12] and their spatial structure was used to identify relevant length scales and locations in the system [13]. In view of the latter, it is therefore possible that a more detailed inspection of the Lyapunov spectrum and the spatial structure of covariant Lyapunov vectors in spatio-temporally chaotic excitable media (as considered in Sect. 3.1.7) could reveal the mechanism underlying the strong size dependence of the effect of heterogeneities. Additionally, they could contain information about the optimal number and location of control sites necessary to suppress chaos.
One way to noninvasively create such control sites in the tissue is via virtual electrodes in response to electric fields. The creation of these secondary sources at tissue boundaries was the subject of Sect. 3.2. A particular sensitivity to electric fields was predicted for negative-curvature boundaries, which correspond to convex tissue regions and therefore outer boundaries of the tissue. The most obvious consequence of the theoretical predictions is that, assuming the electric field is appropriately oriented, the activations that are observed for the lowest field strength, should come from certain locations on the endocardial surface, which has a particularly complex anatomical structure (see introduction). Depending on the concrete spatial arrangement and their attachment to the endocardial surface, trabeculae and papillary muscles can be caricatured as protrusions from the endocardial surface or as cylindrical tissue domains. The non-monotonic shape of the green curve in Fig. 3.27 (p. 130) singles out a particular size from these anatomical features, which is optimal in terms of electric-field sensitivity. The importance of structures that are linked to the bulk of cardiac tissue in distant places for the activation dynamics has already been shown for the Purkinje system, which was reported to have an increased excitability compared to the bulk of tissue due to it being a one-dimensional geometric structure [14]. The results therefore suggest that there are even more structures in the heart that, only due to their geometry, can be excited very easily. Optical mapping studies of the complex endocardial surface could verify this spatially heterogeneous response to electric fields.
With respect to low-energy control of cardiac activity, the results indicate that further significant energy reduction may be achieved by control strategies that aim at inducing wave emission from the above-mentioned structures. However, being located on the endocardium, they provide direct access to a very specific tissue region near the inner surface of the heart, only. Simulations including ongoing activity in the tissue and experiments will have to determine whether control sites on the endocardium could provide an effective way of controlling simpler arrhythmias than fibrillation, e.g., polymorphic or fast ventricular tachycardias, thereby filling the gap in between ATP and LEAP. Additional effects going beyond the scope of the framework presented here can be expected, as dynamical properties such as the action potential duration can be influenced by the presence of boundaries as well [15].
While most of the results presented in Sect. 3.2 are independent of the actual membrane kinetics, because the theory is based on a linearization around the resting state, the simulations for finite pulse duration and different pulse shapes in Sect. 3.2.13 indeed do depend on the specific model. The Fenton-Karma model was chosen because it has been shown to produce results comparable to more detailed, ionic, models. However, quantitatively, this comparability has only been shown for reentry patterns and restitution properties [16], i.e. tissue properties which are defined for propagating action potentials. It is therefore unclear, whether the subthreshold dynamics, which is important for the critical electric field strength determined in Sect. 3.2.13, is realistic, too. Indeed, one degeneracy of the model is that the membrane dynamics is completely passive below the excitation threshold 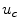 , except for the slow inward current, which activates slowly towards
, except for the slow inward current, which activates slowly towards 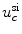 . This absolute passivity leads to the seemingly plausible and large underestimation by the asymptotic theory of the electric field necessary to activate circular boundaries of all curvatures in Fig. 3.35 (p. 143). If the sodium channels responsible for the fast inward current were modeled in a stochastic manner, the force driving the membrane potential back to its resting value would decrease towards the excitation threshold. This could lead to a narrowing of the gap between the critical field strength determined from the numerical simulation and that predicted by the analytical theory.
. This absolute passivity leads to the seemingly plausible and large underestimation by the asymptotic theory of the electric field necessary to activate circular boundaries of all curvatures in Fig. 3.35 (p. 143). If the sodium channels responsible for the fast inward current were modeled in a stochastic manner, the force driving the membrane potential back to its resting value would decrease towards the excitation threshold. This could lead to a narrowing of the gap between the critical field strength determined from the numerical simulation and that predicted by the analytical theory.
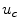 , except for the slow inward current, which activates slowly towards
, except for the slow inward current, which activates slowly towards 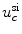 . This absolute passivity leads to the seemingly plausible and large underestimation by the asymptotic theory of the electric field necessary to activate circular boundaries of all curvatures in Fig. 3.35 (p. 143). If the sodium channels responsible for the fast inward current were modeled in a stochastic manner, the force driving the membrane potential back to its resting value would decrease towards the excitation threshold. This could lead to a narrowing of the gap between the critical field strength determined from the numerical simulation and that predicted by the analytical theory.
. This absolute passivity leads to the seemingly plausible and large underestimation by the asymptotic theory of the electric field necessary to activate circular boundaries of all curvatures in Fig. 3.35 (p. 143). If the sodium channels responsible for the fast inward current were modeled in a stochastic manner, the force driving the membrane potential back to its resting value would decrease towards the excitation threshold. This could lead to a narrowing of the gap between the critical field strength determined from the numerical simulation and that predicted by the analytical theory.Most of the results presented in Sect. 3.2 are based on theory and numerical simulations. However, it should be emphasized that there is growing experimental support for the theoretical framework in several aspects: The original theory, developed by A. Pumir and V. Krinsky to describe the effect of circular obstacles in the tissue [2], was not only successfully employed in Sect. 3.3 of this thesis to make experimentally relevant predictions for low-energy stimulation of cardiac tissue, but was also tested in a more direct way using cardiac cell cultures: In her PhD thesis, C. Richter measured critical electric field strengths for the activation of artificial circular obstacles as wave emitting sites in cardiomyocyte cell cultures of neonatal rats [17], thereby confirming the quantitative predictions of the theory (combined with results from [18]). The results of the generalized theory presented in this thesis contain two more predictions which are in line with experimental results: Firstly, the high sensitivity of negative-curvature boundaries was qualitatively confirmed by the cell culture experiments presented in Sect. 3.2.5. Further cell culture studies with carefully-prepared artificial boundaries of known curvature could take this verification to a quantitative level or indicate directions of improvement. Secondly, the reduced time scale for depolarization next to high-curvature circular boundaries found in Sect. 3.2.13 is consistent with a recent study by A. Kondratyev et al., who found a considerably shorter time scale for the rise of the membrane potential in cell cultures of neonatal rat myocytes, if depolarized and hyperpolarized straight boundaries are in close proximity [19]. Thus, a qualitatively similar mechanism seems to be in effect for curved boundaries.
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


