by Philips Healthcare to support the delineation of structures of interest, i.e. the organs at risk [32]).
Computational anatomical phantoms have been reported in the literature since the 1960s. In combination with Monte Carlo methods these computational models are used to simulate complex radiation interactions and energy depositions in the human body. Xu et al. [91] reported 121 different computational phantoms used in radiation protection dosimetry, imaging, radiotherapy etc. until 2009. A general overview of computational phantoms used in radiation dosimetry can be found in [94].
10.2.1 Characterization of Computational Motion Phantoms
Since the late 1990s the incorporation of physiology-dependent organ deformations, like heart-beat or respiratory motion, in computational phantoms is an active and growing area of research. The advantages of computational phantoms in contrast to physical phantoms are realism, flexibility and precision. Computational phantoms provide a ground truth to assess and validate medical image processing algorithms with respect to anatomical variations and with respect to respiration- or heart-beat-driven organ deformations. Furthermore, the models of physiological organ motions in the phantoms can be used as prior knowledge for motion estimation algorithms provided that these models are realistic and general.
Regarding the representation of anatomical structures, computational phantoms can be categorized into three types:
(1)
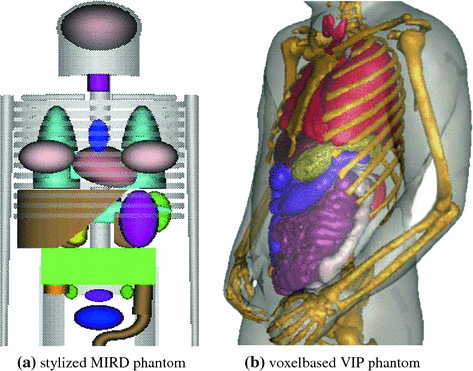
In stylized mathematical representations the organ geometries are represented by simple geometrical shapes. Due to the mathematical definition, these models can easily be manipulated to reflect anatomical variations and organ motion. However the lack of realism makes these models unsuitable for applications in radiotherapy planning. An early model of this type is the mathematical Medical Internal Radiation Dosimetry (MIRD) phantom developed at the Oak Ridge National Laboratory (ORNL) in the 1960s [74] (see Fig. 10.1a). In the following decades a number of gender-, age-, and race-spezific stylized phantoms were developed by different groups in the world [13, 40, 96]. A prominent example of such a model for applications in medical imaging is the 3D and 4D mathematical cardiac torso phantom (MCAT) with gated patient organ information [66].
(2)
Voxel-based representations are based on tomographic images acquired from real individuals. These models consist of segmented images with each voxel labeled with tissue type (e.g. air, bone, soft tissue) and/or anatomical information (lung, leg, liver). Xu [91] reported a total number of 74 phantoms constructed from tomographic data. One of the most detailed and well-known models is the VIP-Man phantom [93] generated from cross sectional photographs of the Visible Human Male cadaver [75] (see Fig. 10.1b). Voxel-based phantoms are very realistic, but they are limited in their abilities to model anatomical variations and organ motion. Furthermore, the necessary segmentation of anatomical structures takes a great amount of work.
(3)
In boundary representation models (BREPs) the outer surface of the anatomical structures are represented by NURBS surfaces or polygon meshes. BREP models are generated from tomographic image data by transforming the voxel representations into smooth surface models. BREPs are able to provide more realistic models of the anatomy and cardiac and respiratory motions than stylized mathematical models, and on the the other hand they offer more flexibility than voxel representations by enabling analytical descriptions of organ deformations and variations. Consequently, most prominent examples of 4D computational phantoms, as the 4D NCAT, 4D XCAT and 4D VIP-Man phantoms [66, 70, 97], belong to this category of representations (see Fig. 10.2).
10.2.1.1 Representation of Respiratory Motion in Computational Phantoms
While organ motion became a critical issue in medical imaging research and radiation therapy, the incorporation of motion information into the computational phantoms was forced. An example for including motion information into stylized phantoms is the 4D MCAT phantom developed for nuclear imaging research, specifically to study the effects of involuntary motion on SPECT and PET [55]. Besides a higher level of realism compared to the MIRD phantom, 4D MCAT models the beating heart and respiration. In this phantom, respiration was modeled by altering the parameters of the geometric models defining diaphragm, lungs, and ribs combined with a translation of heart, liver, stomach, spleen, and kidney.
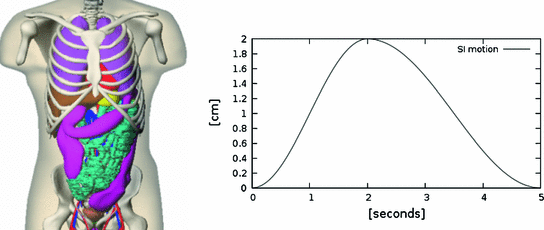
Examples for BREP motion models are the 4D NCAT phantom, 4D XCAT phantom and 4D VIP phantoms [66–68, 90]. These phantoms consist of NURBS-based descriptions of organ surfaces and a software tool to convert the surfaces back to voxelized representations (e.g. simulated CT or SPECT images). NURBS are a very flexible mathematical description and the shape of the NURBS surface can be altered by applying transformations to the associated control points. The modeling of the respiratory motion is based on a respiratory gated 4D CT data set of a normal volunteer. A general motion model for each organ was formulated by tracking landmark points in different regions in the 4D CT data and the derived transformations are applied to the control points of the organ surfaces. By using transformation parameters that are functions of the time 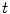 , the control points are extended from 3D to 4D space. For example, in the 4D XCAT and 4D NCAT phantom the motion amplitude of the diaphragm is defined by the function:
, the control points are extended from 3D to 4D space. For example, in the 4D XCAT and 4D NCAT phantom the motion amplitude of the diaphragm is defined by the function:
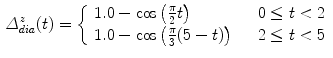
for a respiratory phase of 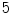 s (
s (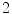 s inhale,
s inhale, 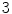 s exhale) and a motion amplitude of
s exhale) and a motion amplitude of 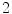 mm (see Fig. 10.2). By altering the parameters of this function, duration and amplitude of respiratory motion can be changed. Due to missing biophysical mechanics in the surface-based modeling approach, the organ transformations are adjusted laboriously to reflect motion dependencies, to avoid surface intersections and to work in concert. For example, the deformation of the lung surface depends on the motion of diaphragm and ribs, or the motion of sternum and skin depends on the rib motion.
mm (see Fig. 10.2). By altering the parameters of this function, duration and amplitude of respiratory motion can be changed. Due to missing biophysical mechanics in the surface-based modeling approach, the organ transformations are adjusted laboriously to reflect motion dependencies, to avoid surface intersections and to work in concert. For example, the deformation of the lung surface depends on the motion of diaphragm and ribs, or the motion of sternum and skin depends on the rib motion.
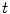 , the control points are extended from 3D to 4D space. For example, in the 4D XCAT and 4D NCAT phantom the motion amplitude of the diaphragm is defined by the function:
, the control points are extended from 3D to 4D space. For example, in the 4D XCAT and 4D NCAT phantom the motion amplitude of the diaphragm is defined by the function: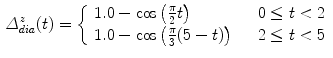
(10.1)
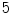 s (
s (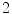 s inhale,
s inhale, 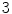 s exhale) and a motion amplitude of
s exhale) and a motion amplitude of 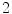 mm (see Fig. 10.2). By altering the parameters of this function, duration and amplitude of respiratory motion can be changed. Due to missing biophysical mechanics in the surface-based modeling approach, the organ transformations are adjusted laboriously to reflect motion dependencies, to avoid surface intersections and to work in concert. For example, the deformation of the lung surface depends on the motion of diaphragm and ribs, or the motion of sternum and skin depends on the rib motion.
mm (see Fig. 10.2). By altering the parameters of this function, duration and amplitude of respiratory motion can be changed. Due to missing biophysical mechanics in the surface-based modeling approach, the organ transformations are adjusted laboriously to reflect motion dependencies, to avoid surface intersections and to work in concert. For example, the deformation of the lung surface depends on the motion of diaphragm and ribs, or the motion of sternum and skin depends on the rib motion.10.2.2 Applications of Computational Motion Phantoms in Radiation Therapy
Early developments in computational phantoms (in the 1960s–1980s) are mostly related to health care physics with the goal to provide recommendations and guidance on radiation protection. So, many stylized and voxel-based phantoms were generated according to the definition of the reference man by the International Commission on Radiological Protection (ICRP) [41]. Mostly, these phantoms are integrated with Monte Carlo methods to simulate radiation transport inside the body and to analyze the energy and patterns of radiation interactions.
In medical radiological imaging applications of computational phantoms are related to the evaluation of image reconstruction algorithms [58, 98], and image quality optimization [24, 31]. 4D motion phantoms were used for the demonstration of imaging artifacts related to cardiac and respiratory organ motions [71] and for the development of reconstruction techniques in 4D PET [42, 87] and 4D CBCT [7].
In radiation therapy, computational motion phantoms were used for the investigation of the spatial and temporal distribution of radiation in the patient body and to gain insight into methods for the management of organ motions. Three effects play a major role in radiation delivery to moving organs: dose blurring, interplay effects and dose deformation [10]. Dose blurring (or smearing) takes place at the field edges where the dose delivered to a point in the patient is smeared or reduced by the motion of this point in and out of the radiation beam resulting in an enlarged beam penumbra. It should be noted that the blurring results as a consequence of both intra- and inter-fractional movements. The interplay effect can occur if the treatment delivery involves moving parts, such as multileaf collimators in IMRT. The third motion effect, dose deformation, is related to the variation of the spatial dose distribution due to the motion of interfaces between structures of different densities. Simulation studies based on computational motion phantoms integrated with 4D Monte Carlo methods [47, 59] have been used for the investigation of these effects because they provide a precise and realistic ground truth with varying motion parameters, like lesion localization, amplitude or frequency of breathing. Zhang et al. [97] used the 4D VIP phantom to study the dosimetric effects of respiratory gating and 4D motion tracking for conformal treatment and IMRT treatment. McGurk et al. [47] investigated IMRT dose distributions as a function of diaphragm motion, lesion size and lung density using the 4D NCAT phantom.
Examples for other applications of computational phantoms in radiation therapy are risk assessment for RT-induced secondary cancer [61, 92], optimal selection of external beam directions [84], or assessment of organ doses in IGRT due to the use of kilovoltage cone-beam computed tomography (kV CBCT) and mega-voltage computed tomography (MV CT) [21].
10.2.3 Limitations of Computational Motion Phantoms
As shown in the last sections, computational phantoms designed to investigate the interaction of radiation with the human body have a remarkable long way. Numerous anatomically realistic computational phantoms were generated since the 1980s, however, the number of realistic computational phantoms incorporating organ motion is limited.
Computational motion phantoms developed so far suffer from limitations that degrade the applicability of these models in radiotherapeutic scenarios. First, the generation of these models is very time-consuming, requiring laborious steps for segmentation, surface modeling and incorporation of organ motion. Then, anatomy and motion information of these models are based on example data. Although some phantoms allow to alter parameters like body size and weight [24], an adaptation of these models to the individual patient anatomy is laborious and time-consuming. Furthermore, they do not have the ability to realistically simulate motion variations that may occur within the same individual or within a population [95]. Third, the motion-related deformation, displacement and interaction of organs is defined geometrically. This geometric definition does not fully take into account inner-organ deformations and the biophysical organ contact mechanics. For example, the respiration-related motion of abdominal organs is represented by a translation in the 4D NCAT phantom and the inner-lung deformation appears to be simplified (see Fig. 10.3).
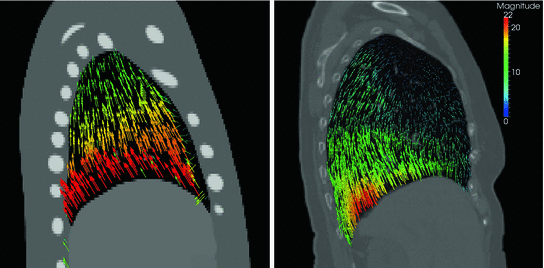

Fig. 10.3
Visualization of deformation fields showing the lung motion between end-inspiration and end-expiration. Left deformation field generated with the 4D NCAT phantom. Right deformation field estimated with DIR based on patient-specific 4D CT data (right)
In this context, Xu et al. identified two main directions in future research related to computational motion phantoms [95]: (1) the efficient generation of individual, patient-specific models and (2) the incorporation of biophysical modeling techniques to allow for realistic physics-based organ deformations. First steps to generate patient-specific computerized phantoms were presented by Segars et al. and Tward et al. by applying diffeomorphic registration algorithms to map a computational phantom to patient-specific data sets [69, 79]. Using this technique it is possible to create a detailed patient-specific model within 1–2 days. Biophysical modeling techniques were discussed in Chap. 4. As pointed out there, biophysical models provide powerful tools to simulate respiratory mechanics, however, recent studies show that in terms of accuracy and applicability these models were outperformed by DIR algorithms in motion estimation for individual 4D image data.
In the rest of this chapter, we will discuss an alternative approach to generate respiratory motion models that have the potential to overcome some limitations of classical computerized anatomical phantoms.
10.3 Generation of Population-Based Motion Models
Computational motion phantoms discussed in Sect. 10.2 consist of a single reference data set or a small number of reference data sets build from example image data. In contrast, population-based motion models aim to represent anatomical variations and motion variations in a population of 4D images. These models consist of a “mean” representation and a variation model describing variations in the population. In medical image processing, this concept is used commonly for image segmentation and classification with statistical shape models [26].
By the increasing accessibility of 4D imaging techniques in the clinic, 4D patient data is more and more available, and the generation of population-based models of organ motion becomes feasible. As shown in Sect. 10.2, the generation of a single full-body motion model with a high level of anatomical detail is a time-consuming and laborious work. Population-based models rely on automatic algorithms to process a considerable amount of image data in the patient pool. With the availability of automatic segmentation and registration algorithms in the last years, the generation of such models was possible at least for a fraction of the body and a small number of organs, e.g. lung and/or liver [18, 38, 73].
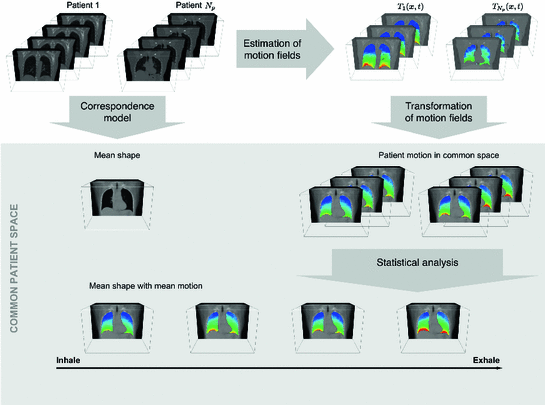

Fig. 10.4
Principal idea of statistical inter-patient models: Given is a set of 4D images from different patients, the motion information is extracted from the 4D images, and correspondence between the different patient anatomies is established to define a common coordinate space. The computed motion fields are transformed into the common coordinate space and a statistical model of the motion information in the data sets is computed
Four steps are needed to generate population-based motion models: (1) acquisition of a set of 4D images, (2) the motion information is extracted from the 4D images, and (3) correspondence between the different images is established to (4) compute a statistical model of motion information in the data sets.
The 4D images can be acquired from different patients or from the same patient in repeated sessions. Figure 10.4 visualizes the principal idea of statistical inter-patient models. For intra-patient models the same four steps have to be performed and the correspondence model has to account for pose variations of the patient in the scanner.
In contrast to the geometrical definition of organ motion in stylized or BREP-based phantoms (see Sect. 10.2.1.1), the population-based approach generates a statistical description of the organ motion including a mean and variance. In the context of radiation therapy, such a model has the potential to allow for the estimation of uncertainties introduced by inter- and intra-fractional respiratory motion variability (see Sect. 10.4.3).
10.3.1 Variability of Respiratory Motion
Day-to-day and breath-to-breath variations of respiratory motion form an important problem in RT. To cope with such inter- and intra-fractional motion variations, a number of approaches were developed to relate internal motion to external surrogate signals, as skin motion (e.g. [65, 82]) or tidal volume and air-flow [43]. Those models were discussed in Chap. 9 in detail. The majority of these models use a single 4D data set representing a single breathing cycle and therefore, the representation of intra- and inter-fractional variations is limited. If repeatedly acquired 4D images are available for the patient, a population-based intra-patient model can be build from the ensemble of motion data sets and can therefore cover a broader range of motion patterns.
However, the availability of multiple 4D image data sets for a single patient is very limited, and the questions raises whether motion information of different patients can be combined to generate prior knowledge about respiratory lung motion. In Fig. 10.5, the magnitude of respiratory lung motion between maximum inhale and maximum exhale is visualized color-coded for different patients. As shown in this figure, there is an anatomical variation regarding shape and size of the lungs and a variation in magnitude and pattern of respiratory motion, but the overall pattern of respiratory motion of different patient is similar: large deformations near diaphragm and small deformations near the tip of the lung. Thus, inter-patient population-based modeling approaches rely on the assumption, that breathing dynamics works similarly for all patients and useful statistical information can be generated.
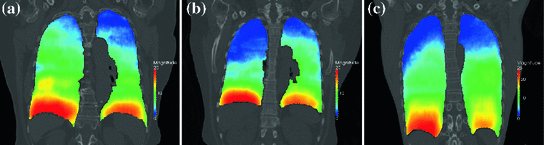

Fig. 10.5
Examples of computed breathing motion displacement fields. The magnitude of the estimated lung motion between end expiration and end inspiration is visualized color coded (in mm). The lung geometry and motion amplitude differ between patients, motion patterns appear to be similar
Accordingly, population-based models can be roughly divided into models derived from ensembles of 4D images of the same patient or from ensembles of 4D images from different patients. For models of the first category, 4D images have to be acquired repeatedly for one patient, for example 4D CT data set repeatedly acquired during the course of treatment were used in [38], or 4D CT images and additional 4D MR images can be acquired before the treatment alternatively [8, 14, 36]. For models of the second category, 4D images of different patients are combined to one motion model with the advantage that no additional effort, costs and irradiation dose is needed for each patient, and the pool of available data for model generation growth continuously. All steps shown in Fig. 10.4 have to be performed for both types of models. However, in the case of subject-specific models rigid or affine transformations can be used to compensate for different positions of the subject in the CT or MR scanner, whereas establishing correspondence between different subjects is a challenging task due to anatomical variations and missing correspondences in the presence of pathological structures.
10.3.2 Estimation of Motion Fields
Given is a pool of 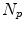 4D images (from one or different patients) to generate the population-based motion model. Each 4D image in the pool consists of a sequence of
4D images (from one or different patients) to generate the population-based motion model. Each 4D image in the pool consists of a sequence of 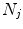 3D images
3D images 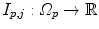 (
(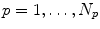 ) acquired at different phases
) acquired at different phases 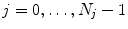 of the breathing cycle, as introduced in Chap. 2.
of the breathing cycle, as introduced in Chap. 2.
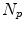 4D images (from one or different patients) to generate the population-based motion model. Each 4D image in the pool consists of a sequence of
4D images (from one or different patients) to generate the population-based motion model. Each 4D image in the pool consists of a sequence of 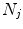 3D images
3D images 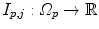 (
(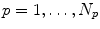 ) acquired at different phases
) acquired at different phases 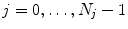 of the breathing cycle, as introduced in Chap. 2.
of the breathing cycle, as introduced in Chap. 2.For each 4D data set, the motion represented in the images has to be estimated. Registration-based algorithms for motion estimation are discussed in Chaps. 4–7. Depending on the choice of registration method, different representations of the motion information are generated. Intensity-based registration approaches (Chaps. 6 and 7) compute dense motion fields where deformations are given for each voxel. Surface- and feature-based registration approaches as introduced in Chap. 5 generate point-based representations where displacements are given for distinct feature-points or sampled points on the organ surface only. However, both representations can be transferred into each other by sampling the dense motion field at a subset of voxels or by an interpolation of sparse motion fields (see Chap. 5.4).
The computed motion fields for the 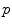 -th 4D image define transformations
-th 4D image define transformations 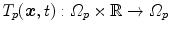 of the specific coordinate system
of the specific coordinate system 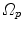 modeling the motion-related organ deformation for a time
modeling the motion-related organ deformation for a time 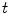 . In most approaches, these transformations are given only for discrete time-points
. In most approaches, these transformations are given only for discrete time-points 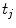 associated with a state
associated with a state 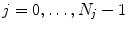 in the breathing cycle. In surface- or landmark-based representations, the deformations are known only for distinct points.
in the breathing cycle. In surface- or landmark-based representations, the deformations are known only for distinct points.
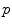 -th 4D image define transformations
-th 4D image define transformations 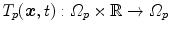 of the specific coordinate system
of the specific coordinate system 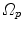 modeling the motion-related organ deformation for a time
modeling the motion-related organ deformation for a time 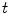 . In most approaches, these transformations are given only for discrete time-points
. In most approaches, these transformations are given only for discrete time-points 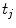 associated with a state
associated with a state 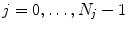 in the breathing cycle. In surface- or landmark-based representations, the deformations are known only for distinct points.
in the breathing cycle. In surface- or landmark-based representations, the deformations are known only for distinct points.As discussed in Chap. 9, in most approaches, the organ deformations are expressed with respect to a baseline image for a reference point in the breathing cycle, e.g. with respect to 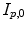 , and
, and 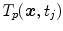 describes the organ deformation between breathing phase 0 and phase
describes the organ deformation between breathing phase 0 and phase 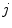 . The transformation
. The transformation 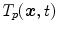 is usually represented by displacement vectors
is usually represented by displacement vectors 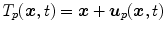 (defined voxel-wise or for distinct points only) and the statistical analysis of organ deformations is based on the displacement vectors
(defined voxel-wise or for distinct points only) and the statistical analysis of organ deformations is based on the displacement vectors 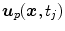 at discrete phases
at discrete phases 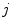 . Other representations of organ deformations are possible. McClelland et al. presents a time-continuous motion representation of
. Other representations of organ deformations are possible. McClelland et al. presents a time-continuous motion representation of 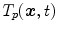 based on a B-spline approximation [46]. Ehrhardt et al. proposes the use of diffeomorphisms for motion representation and statistics [18], and Klinder et al. compares the application of explicit point coordinates, displacements, and fourier descriptors for motion modeling [39]. The different representations have different advantages and disadvantages and at present, it is not known in advance which is the most suitable representation for a given problem. We will discuss the differences in point-based representations by displacement vectors and voxel-based representations by diffeomorphisms in more detail in Sects. 10.4.1 and 10.4.2. Examples for population-based motion models and their applied motion estimation algorithms and motion representations are summarized in Table 10.1.
based on a B-spline approximation [46]. Ehrhardt et al. proposes the use of diffeomorphisms for motion representation and statistics [18], and Klinder et al. compares the application of explicit point coordinates, displacements, and fourier descriptors for motion modeling [39]. The different representations have different advantages and disadvantages and at present, it is not known in advance which is the most suitable representation for a given problem. We will discuss the differences in point-based representations by displacement vectors and voxel-based representations by diffeomorphisms in more detail in Sects. 10.4.1 and 10.4.2. Examples for population-based motion models and their applied motion estimation algorithms and motion representations are summarized in Table 10.1.
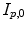 , and
, and 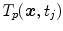 describes the organ deformation between breathing phase 0 and phase
describes the organ deformation between breathing phase 0 and phase 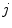 . The transformation
. The transformation 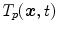 is usually represented by displacement vectors
is usually represented by displacement vectors 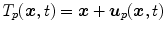 (defined voxel-wise or for distinct points only) and the statistical analysis of organ deformations is based on the displacement vectors
(defined voxel-wise or for distinct points only) and the statistical analysis of organ deformations is based on the displacement vectors 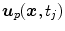 at discrete phases
at discrete phases 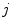 . Other representations of organ deformations are possible. McClelland et al. presents a time-continuous motion representation of
. Other representations of organ deformations are possible. McClelland et al. presents a time-continuous motion representation of 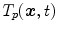 based on a B-spline approximation [46]. Ehrhardt et al. proposes the use of diffeomorphisms for motion representation and statistics [18], and Klinder et al. compares the application of explicit point coordinates, displacements, and fourier descriptors for motion modeling [39]. The different representations have different advantages and disadvantages and at present, it is not known in advance which is the most suitable representation for a given problem. We will discuss the differences in point-based representations by displacement vectors and voxel-based representations by diffeomorphisms in more detail in Sects. 10.4.1 and 10.4.2. Examples for population-based motion models and their applied motion estimation algorithms and motion representations are summarized in Table 10.1.
based on a B-spline approximation [46]. Ehrhardt et al. proposes the use of diffeomorphisms for motion representation and statistics [18], and Klinder et al. compares the application of explicit point coordinates, displacements, and fourier descriptors for motion modeling [39]. The different representations have different advantages and disadvantages and at present, it is not known in advance which is the most suitable representation for a given problem. We will discuss the differences in point-based representations by displacement vectors and voxel-based representations by diffeomorphisms in more detail in Sects. 10.4.1 and 10.4.2. Examples for population-based motion models and their applied motion estimation algorithms and motion representations are summarized in Table 10.1.Table 10.1
Population-based respiratory motion models used for applications in radiation therapy
Year | Reference | Organ and data | Motion estimation algorithm | Motion representation | Correspondence model | Statistical model |
|---|---|---|---|---|---|---|
2004 | Sundaram et al. [76] | Lung (2D+t MR) | Intensity-based registration | Voxel-based, displacement vectors | Explicit, non-linear registration between all subjects | Average lung motion model |
2007 | von Siebenthal et al. [73] | Liver (4D MRI) | Intensity-based registration | Point-based, displacement vectors at landmarks inside liver | Implicit, manual fitting of a liver model and landmark extraction, rigid alignment of all data sets before statistical analysis | PCA (liver drift model) |
2008 | Ehrhardt et al. [19] | Lung (4D CT) | Intensity-based registration | Voxel-based, displacement vectors | Explicit, non-linear registration to an atlas, affine alignment of motion vectors | Mean motion |
2009 | Klinder et al. [38] | Lung (4D CT) | Surface-based registration | Point-based, displacement vectors at mesh positions | Implicit, fitting a surface mesh to all data sets, affine alignment of motion vectors | PCA (intra- and inter-patient) |
2009 | Nguyen et al. [51] | Liver (4D CT) | FEM-based registration (MORFEUS) | Point-based, displacement vectors at the nodes of FE mesh | Implicit, fitting a FE mesh to all subjects, rigid alignment of motion vectors | Mean motion |
2010 | He et al. [25] | Lung (4D CT) | Joint segmentation and registration framework | Point-based, displacement vectors at landmark positions | Explicit, non-linear registration to a template image, affine alignment of motion vectors | K-PCA |
2011 | Ehrhardt et al. [18] | Lung (4D CT) | Diffeomorphic, intensity-based registration | Voxel-based, diffeomorphism represented by static velocity field | Explicit, diffeomorphic registration to an atlas, non-linear alignment of motion vectors | Mean motion (diffeomorphic) |
2012 | Preiswerk et al. [54] | Liver (4D MRI) | Intensity-based registration | Point-based, displacement vectors at feature points inside the liver | Implicit, manual fitting of a liver model and landmark extraction, rigid alignment of motion vectors | PCA |
10.3.3 The Correspondence Problem
The motion-related organ deformation of each subject (data set) is described within its own reference frame. This reference frame is defined by the imaging process, i.e. the computed transformations 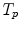 and
and 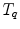 of two subjects
of two subjects 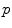 and
and 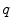 are defined with respect to the underlying image spaces
are defined with respect to the underlying image spaces 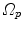 and
and 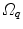 . This is the case too, if the same subject is imaged twice due to the different positions of the subject in the CT or MR scanner.
. This is the case too, if the same subject is imaged twice due to the different positions of the subject in the CT or MR scanner.
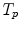 and
and 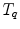 of two subjects
of two subjects 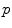 and
and 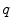 are defined with respect to the underlying image spaces
are defined with respect to the underlying image spaces 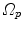 and
and 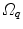 . This is the case too, if the same subject is imaged twice due to the different positions of the subject in the CT or MR scanner.
. This is the case too, if the same subject is imaged twice due to the different positions of the subject in the CT or MR scanner.To analyze the spatiotemporal variability in a population, we need to compare the deformation of organ-shapes over time and across subjects. In order to compare two deformation functions 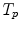 and
and 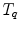 anatomical correspondence between the organ shapes has to be defined, i.e. the comparison of
anatomical correspondence between the organ shapes has to be defined, i.e. the comparison of 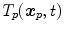 and
and 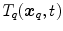 only makes sense if
only makes sense if 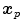 and
and 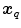 refer to identical anatomical localizations. Furthermore, a temporal correspondence is needed this means
refer to identical anatomical localizations. Furthermore, a temporal correspondence is needed this means 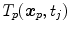 and
and 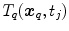 have to refer to the same breathing state for given
have to refer to the same breathing state for given 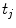 . Several choices can be made to define temporal consistency, e.g. by (i) mapping selected time points in the breathing cycle (e.g. end-expiration) and regular partitioning in between (phase-based sorting), or by (ii) mapping according to the percentage lung volume change (amplitude-based sorting), or by (iii) mapping according to a morphological configuration, e.g. diaphragm position. The choice depends on the application purpose of the breathing model and on quantities that can be measured during application. Here, we assume that the temporal consistency is ensured during the image acquisition, e.g. by sorting into corresponding bins for all subjects (see Chaps. 1–3), or in a preprocessing step, e.g. by using a method described by Sundaram et al. [76, 77].
. Several choices can be made to define temporal consistency, e.g. by (i) mapping selected time points in the breathing cycle (e.g. end-expiration) and regular partitioning in between (phase-based sorting), or by (ii) mapping according to the percentage lung volume change (amplitude-based sorting), or by (iii) mapping according to a morphological configuration, e.g. diaphragm position. The choice depends on the application purpose of the breathing model and on quantities that can be measured during application. Here, we assume that the temporal consistency is ensured during the image acquisition, e.g. by sorting into corresponding bins for all subjects (see Chaps. 1–3), or in a preprocessing step, e.g. by using a method described by Sundaram et al. [76, 77].
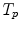 and
and 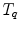 anatomical correspondence between the organ shapes has to be defined, i.e. the comparison of
anatomical correspondence between the organ shapes has to be defined, i.e. the comparison of 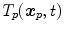 and
and 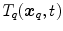 only makes sense if
only makes sense if 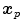 and
and 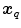 refer to identical anatomical localizations. Furthermore, a temporal correspondence is needed this means
refer to identical anatomical localizations. Furthermore, a temporal correspondence is needed this means 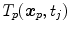 and
and 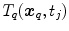 have to refer to the same breathing state for given
have to refer to the same breathing state for given 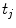 . Several choices can be made to define temporal consistency, e.g. by (i) mapping selected time points in the breathing cycle (e.g. end-expiration) and regular partitioning in between (phase-based sorting), or by (ii) mapping according to the percentage lung volume change (amplitude-based sorting), or by (iii) mapping according to a morphological configuration, e.g. diaphragm position. The choice depends on the application purpose of the breathing model and on quantities that can be measured during application. Here, we assume that the temporal consistency is ensured during the image acquisition, e.g. by sorting into corresponding bins for all subjects (see Chaps. 1–3), or in a preprocessing step, e.g. by using a method described by Sundaram et al. [76, 77].
. Several choices can be made to define temporal consistency, e.g. by (i) mapping selected time points in the breathing cycle (e.g. end-expiration) and regular partitioning in between (phase-based sorting), or by (ii) mapping according to the percentage lung volume change (amplitude-based sorting), or by (iii) mapping according to a morphological configuration, e.g. diaphragm position. The choice depends on the application purpose of the breathing model and on quantities that can be measured during application. Here, we assume that the temporal consistency is ensured during the image acquisition, e.g. by sorting into corresponding bins for all subjects (see Chaps. 1–3), or in a preprocessing step, e.g. by using a method described by Sundaram et al. [76, 77].10.3.3.1 Anatomical Correspondence
Statistical motion analysis in a pool of 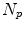 4D data sets necessitate to establish correspondence between all subjects. One approach is to extract corresponding landmark positions in all subjects, as proposed by Siebenthal et al. and Arnold et al. for a liver motion model [2, 73]. Klinder et al. propagate a structurally identical deformable surface mesh to all patient data sets [38]. This surface mesh was generated by averaging lung segmentations of training data sets [9] and is used for lung segmentation and motion estimation simultaneously. Nguyen et al. generate a finite element mesh of the liver from combined binary mask of training data sets. The finite element mesh is fitted to each patient data sets using a FEM-based deformable surface registration [51]. We refer to those approaches by implicit correspondence, because identical sets of features (landmarks or surface meshes) are propagated to each 4D data set in the population, and correspondence is given by the mapping of corresponding features. But implicit correspondence alone is not sufficient for a statistical analysis. As shown in Fig. 10.6, the orientation of structures inside the image space influences the direction of the displacement vectors. Therefore, it is necessary to bring the 4D images in the population into a common coordinate system before a statistical analysis.
4D data sets necessitate to establish correspondence between all subjects. One approach is to extract corresponding landmark positions in all subjects, as proposed by Siebenthal et al. and Arnold et al. for a liver motion model [2, 73]. Klinder et al. propagate a structurally identical deformable surface mesh to all patient data sets [38]. This surface mesh was generated by averaging lung segmentations of training data sets [9] and is used for lung segmentation and motion estimation simultaneously. Nguyen et al. generate a finite element mesh of the liver from combined binary mask of training data sets. The finite element mesh is fitted to each patient data sets using a FEM-based deformable surface registration [51]. We refer to those approaches by implicit correspondence, because identical sets of features (landmarks or surface meshes) are propagated to each 4D data set in the population, and correspondence is given by the mapping of corresponding features. But implicit correspondence alone is not sufficient for a statistical analysis. As shown in Fig. 10.6, the orientation of structures inside the image space influences the direction of the displacement vectors. Therefore, it is necessary to bring the 4D images in the population into a common coordinate system before a statistical analysis.
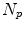 4D data sets necessitate to establish correspondence between all subjects. One approach is to extract corresponding landmark positions in all subjects, as proposed by Siebenthal et al. and Arnold et al. for a liver motion model [2, 73]. Klinder et al. propagate a structurally identical deformable surface mesh to all patient data sets [38]. This surface mesh was generated by averaging lung segmentations of training data sets [9] and is used for lung segmentation and motion estimation simultaneously. Nguyen et al. generate a finite element mesh of the liver from combined binary mask of training data sets. The finite element mesh is fitted to each patient data sets using a FEM-based deformable surface registration [51]. We refer to those approaches by implicit correspondence, because identical sets of features (landmarks or surface meshes) are propagated to each 4D data set in the population, and correspondence is given by the mapping of corresponding features. But implicit correspondence alone is not sufficient for a statistical analysis. As shown in Fig. 10.6, the orientation of structures inside the image space influences the direction of the displacement vectors. Therefore, it is necessary to bring the 4D images in the population into a common coordinate system before a statistical analysis.
4D data sets necessitate to establish correspondence between all subjects. One approach is to extract corresponding landmark positions in all subjects, as proposed by Siebenthal et al. and Arnold et al. for a liver motion model [2, 73]. Klinder et al. propagate a structurally identical deformable surface mesh to all patient data sets [38]. This surface mesh was generated by averaging lung segmentations of training data sets [9] and is used for lung segmentation and motion estimation simultaneously. Nguyen et al. generate a finite element mesh of the liver from combined binary mask of training data sets. The finite element mesh is fitted to each patient data sets using a FEM-based deformable surface registration [51]. We refer to those approaches by implicit correspondence, because identical sets of features (landmarks or surface meshes) are propagated to each 4D data set in the population, and correspondence is given by the mapping of corresponding features. But implicit correspondence alone is not sufficient for a statistical analysis. As shown in Fig. 10.6, the orientation of structures inside the image space influences the direction of the displacement vectors. Therefore, it is necessary to bring the 4D images in the population into a common coordinate system before a statistical analysis.
Fig. 10.6
Transformation of motion fields between two patient coordinate systems 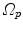 and
and 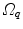 . Beside the anatomical correspondence, an adjustment and reorientation of the motion vectors is performed with Eq. (10.2) to account for position, size, and shape variations
. Beside the anatomical correspondence, an adjustment and reorientation of the motion vectors is performed with Eq. (10.2) to account for position, size, and shape variations
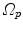 and
and 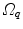 . Beside the anatomical correspondence, an adjustment and reorientation of the motion vectors is performed with Eq. (10.2) to account for position, size, and shape variations
. Beside the anatomical correspondence, an adjustment and reorientation of the motion vectors is performed with Eq. (10.2) to account for position, size, and shape variationsIn contrast, explicit correspondence is defined by mapping functions 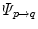 and
and 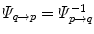 between the reference frames
between the reference frames 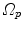 and
and 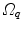 computed by registration algorithms. Because deformations in 4D image sequences are often expressed with respect to the baseline image
computed by registration algorithms. Because deformations in 4D image sequences are often expressed with respect to the baseline image 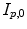 , several approaches applying correspondence between 4D image sequences of different subjects by a 3D registration of baseline images
, several approaches applying correspondence between 4D image sequences of different subjects by a 3D registration of baseline images 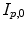 and
and 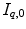 [12, 18, 56]. Some explicit correspondence methods select one target to which all other subjects are registered or deformed, e.g. [25]. This, however biases the registration result to the selected shape. Different strategies were proposed to minimize this bias, e.g. by selecting a subject that lies closest to the mean shape [52], or by evolving a mean shape [23, 29]. Other explicit approaches aim to take into account the full temporal information to register two 4D image sequences. Peyrat et al. [53] proposes a 4D–4D registration by computing deformations between any pair of scans of two different subjects at the same time-point simultaneously via a multi-channel co-registration. A more general approach proposed by Durrleman et al. does not require that subjects are scanned the same number of times or at the same time points, and computes spatial and temporal correspondences simultaneously [16].
[12, 18, 56]. Some explicit correspondence methods select one target to which all other subjects are registered or deformed, e.g. [25]. This, however biases the registration result to the selected shape. Different strategies were proposed to minimize this bias, e.g. by selecting a subject that lies closest to the mean shape [52], or by evolving a mean shape [23, 29]. Other explicit approaches aim to take into account the full temporal information to register two 4D image sequences. Peyrat et al. [53] proposes a 4D–4D registration by computing deformations between any pair of scans of two different subjects at the same time-point simultaneously via a multi-channel co-registration. A more general approach proposed by Durrleman et al. does not require that subjects are scanned the same number of times or at the same time points, and computes spatial and temporal correspondences simultaneously [16].
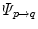 and
and 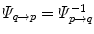 between the reference frames
between the reference frames 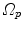 and
and 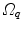 computed by registration algorithms. Because deformations in 4D image sequences are often expressed with respect to the baseline image
computed by registration algorithms. Because deformations in 4D image sequences are often expressed with respect to the baseline image 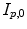 , several approaches applying correspondence between 4D image sequences of different subjects by a 3D registration of baseline images
, several approaches applying correspondence between 4D image sequences of different subjects by a 3D registration of baseline images 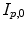 and
and 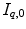 [12, 18, 56]. Some explicit correspondence methods select one target to which all other subjects are registered or deformed, e.g. [25]. This, however biases the registration result to the selected shape. Different strategies were proposed to minimize this bias, e.g. by selecting a subject that lies closest to the mean shape [52], or by evolving a mean shape [23, 29]. Other explicit approaches aim to take into account the full temporal information to register two 4D image sequences. Peyrat et al. [53] proposes a 4D–4D registration by computing deformations between any pair of scans of two different subjects at the same time-point simultaneously via a multi-channel co-registration. A more general approach proposed by Durrleman et al. does not require that subjects are scanned the same number of times or at the same time points, and computes spatial and temporal correspondences simultaneously [16].
[12, 18, 56]. Some explicit correspondence methods select one target to which all other subjects are registered or deformed, e.g. [25]. This, however biases the registration result to the selected shape. Different strategies were proposed to minimize this bias, e.g. by selecting a subject that lies closest to the mean shape [52], or by evolving a mean shape [23, 29]. Other explicit approaches aim to take into account the full temporal information to register two 4D image sequences. Peyrat et al. [53] proposes a 4D–4D registration by computing deformations between any pair of scans of two different subjects at the same time-point simultaneously via a multi-channel co-registration. A more general approach proposed by Durrleman et al. does not require that subjects are scanned the same number of times or at the same time points, and computes spatial and temporal correspondences simultaneously [16].It is obvious that anatomical correspondence for intra-patient models is easier to define, whereas inter-patient registration has to deal with high-dimensional transformations and varying anatomies. A further shortcoming of current methods for inter-subject correspondences is that the accuracy of these methods is widely unknown. Although, a number of attempts exists to assess accuracy and robustness of registration techniques for intra-patient registration and motion estimation, e.g. the MIDRAS and EMPIRE10 studies [11, 49] (see Chap. 8), similar evaluation studies for inter-subject registration are missing. One reason is the difficulty to define an accurate ground truth: due to the anatomical variability, definition of a sufficiently large number of corresponding landmarks between subjects is a challenging task. The assessment of inter-patient registration methods is an ongoing topic of research, but available evaluations suggest an accuracy in the order of the inter-observer variability [27, 37].
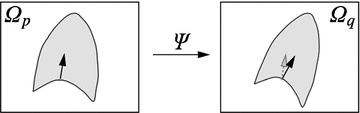
10.3.3.2 Transformation of the Motion Fields 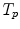
The computed motion fields have to be transformed into a common coordinate system before a statistical analysis to eliminate subject-specific orientation information (see Fig. 10.6). A general formulation is given as follows: Given a transformation 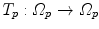 and a homeomorphism
and a homeomorphism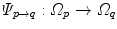 between the coordinate systems
between the coordinate systems 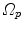 and
and 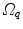 , then
, then 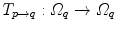 is the topologically conjugate of
is the topologically conjugate of 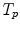 , if
, if
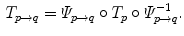 < div class='tao-gold-member'>
< div class='tao-gold-member'>




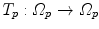 and a homeomorphism
and a homeomorphism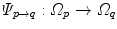 between the coordinate systems
between the coordinate systems 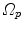 and
and 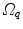 , then
, then 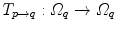 is the topologically conjugate of
is the topologically conjugate of 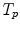 , if
, if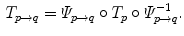
Only gold members can continue reading. Log In or Register to continue
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree