Fig. 10.1
GRE pulse sequence with resulting magnetization displayed at the bottom
What Is the FID?
Once the externally-applied RF signal has ended, H1 spins will realign such that the net magnetic moment (M) is parallel to B0. During relaxation these H1 spins lose energy by emitting their own RF signal, which is referred to as the free-induction decay (FID) response signal. These FIDs are measured by the receive coils placed around the body. The strength of the FID is dependent on the proton density of the tissue being imaged, the longitudinal relaxation time (T1), and the transverse relaxation time (T2). In theory, T2 can be measured directly as the mono-exponential decay rate of the signal in a perfectly homogeneous magnetic field. By purposely applying magnetic field gradients, for example by slightly increasing the magnetic field experienced by the left side of the patient’s body compared to the right side, the signal is forced to decay more quickly. Subsequent reversal of the gradient direction from left-right to right-left causes the formation of echoes (Fig. 10.1: Signal). The frequency components of these echoes contain information about spatial location, i.e. information regarding how much signal originated from the left versus right side of the patient’s body, and therefore can be used to build an image.
What Are Echoes?
Unlike in a traditional spin-echo pulse sequence that uses 180° refocusing pulses, a gradient echo pulse sequence requires a bipolar readout gradient. This is achieved by first applying a dephasing gradient followed by the frequency-encoding readout gradient. The dephasing stage is inverse in sign and half the area of the frequency encoding gradient (see Fig. 10.1: Gx). This is designed such that the first half of the frequency-encoding gradient inverts the dephasing created by the negative lobe, and the peak of the echo occurs at the middle of the readout gradient (i.e. echo time (TE), Fig. 10.1: Signal).
Spoiled Gradient Echo Imaging (SPGR, FGRE, etc.)
The T1 and T2 times in the tissues involved in cardiac imaging are generally in the range of tens to hundreds of milliseconds. This means there is significant signal remaining in the transverse plane for repetition times normally used in cardiac imaging. In order to allow for fast cardiac imaging using GRE pulse sequences, the remaining magnetization should be ‘spoiled’ so it does not contaminate subsequent phase encoding steps. This can be accomplished either with gradient spoiling, which allows for shorter overall TR, or RF spoiling, which can facilitate T1 weighting throughout the image acquisition.
Gradient Spoiling (Shortens TR)
Gradient spoiling is commonly used in cardiac imaging to destroy the residual transverse magnetization following each readout (Fig. 10.2). This is necessary to prevent transverse magnetization from previous RF pulses from contaminating subsequent readouts (known as stimulated echoes). The downside of gradient spoiling is the dephased spins no longer contribute to subsequent MR signals. Since the T1 and T2 of myocardium and blood are long, and TR is short, low flip angles are necessary to prevent loss of signal due to gradient spoiling [1].
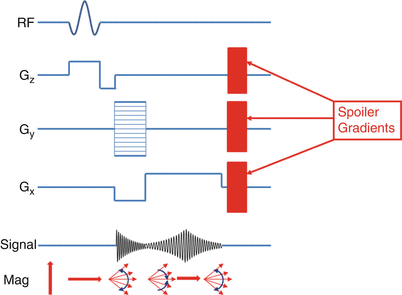

Fig. 10.2
Spoiled GRE pulse sequence showing spoiler gradients added at the end of each RF pulse
RF Spoiling
RF spoiling can also be referred to as RF pulse phase cycling. This takes advantage of the fact that the RF pulse can be played at any phase (i.e. direction in the x-y plane) and the refocusing occurs at that phase location. Therefore, if the RF pulse is played at a random phase, the likelihood that a stimulated echo will rephase at the same location is greatly reduced. In most practical applications the RF pulses played in a series of TRs are pseudo-random, incrementing phase quadratically to provide better spatially and temporally invariant spoiling than either gradient spoiling or completely random RF spoiling [2].
Signal Equation
The signal for a spoiled-GRE sequence depends on sequence-selectable variables (TR, TE, and flip angle (α)), along with three variables intrinsic to the tissue being imaged (T1, T2*, and spin density [H]). We have introduced a new term, T2*, rather than T2 since the spoiled-GRE sequence does not account for field inhomogeneities as a spin-echo sequence would. Assuming we have reached a steady-state (see below) and have achieved perfect spoiling, the signal (S) of a spoiled-GRE sequence is given in Eq. 10.1
![$$ S=k\left[H\right]\frac{ \sin a\left(1-{e}^{-TR/{T}_1}\right)}{\left(1-\left( \cos a\right){e}^{--TR/{T}_1}\right)}{e}^{-TE/{T}_2*} $$](/wp-content/uploads/2016/07/A315651_1_En_10_Chapter_Equ1.gif)
where k is a scaling factor. The first term (k[H]) accounts for spin-density effects, the second term contributes to the T1 weighting of the image, and the third term contributes to T2* weighting. From this, it is clear to see how α, TR, and TE contribute to T1 and T2* weighting in spoiled-GRE sequences. As α decreases, the T1 effect is reduced (1-e−TR/T1 term cancels), and we are left with [H] and T2*. If TR is long and TE is minimized, we are left with a proton-density weighted image. As the TE is increased, the amount of T2* weighting is increased. Conversely, as TR is decreased the amount of T1 weighting actually increases (e−TR/T1 term becomes large). Finally, if the TE is kept short (minimize T2*) and TR is short as well, α can be used to increase T1 weighting as is given below [3].
![$$ S=k\left[H\right]\frac{ \sin a\left(1-{e}^{-TR/{T}_1}\right)}{\left(1-\left( \cos a\right){e}^{--TR/{T}_1}\right)}{e}^{-TE/{T}_2*} $$](/wp-content/uploads/2016/07/A315651_1_En_10_Chapter_Equ1.gif)
(10.1)
To obtain the maximum signal, the optimal flip angle, called the Ernst angle (αE), can be calculated by setting dS/dα = 0 above.
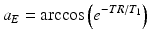
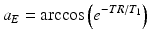
(10.2)
Saturation and In-Flow Effects
Using the explanation of spoiled-GRE signal and optimal flip angle above, it is easy to see how an aggressively high flip angle would tend to saturate the resulting spoiled-GRE signal. This saturation is more noticeable with shorter repetition times as are used for cardiac imaging. Basically, the acquisition is not allowing enough T1 recovery between high flip angle RF pulses, so the majority of the MR signal is being spoiled, thus no longer contributing to subsequent MR signals.
The preceding derivation assumes everything within the imaging space has reached a steady-state. A more detailed description of steady-state imaging is provided below. For the discussion on inflow effects let’s assume we are operating in a steady-state regime, which means the Mz signal returns to a consistent level between RF pulses. Now, assume there is inflowing blood from another part of the body, which has not been exposed to these RF pulses, and thus enters the imaging plane with a higher starting Mz than in-slice tissue. This results in a portion of the imaging plane not being in steady-state which manifests itself as signal inhomogeneities throughout the image (see blood pool in Fig. 10.3). The severity of this artifact is related to the tissue characteristics and imaging parameters chosen. The more saturated the steady-state signal (increased α, decreased TR), the larger the difference in Mz between steady-state and inflowing tissue, the more heterogeneous the signal appears [4].
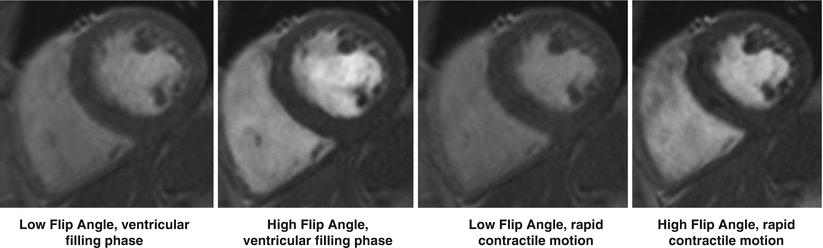

Fig. 10.3
Effects of high flip angle on spoiled GRE cine imaging. Note the heterogeneous blood signal during ventricular filling phase (left) due to inflowing spins. Right: myocardial heterogeneity due to rapid cardiac motion during relaxation
Time to Steady State and the Role of Dummy Heartbeats
Performing spoiled GRE imaging requires the transverse and longitudinal magnetization to have achieved a steady state. This limits the fluctuation in magnetization from one RF pulse to the next. The time it takes to reach a steady state depends on the MR parameters chosen (TR and flip angle) and inherent tissue properties such as T1.
To determine how many dummy RF pulses are required to reach steady-state, an experiment of repeated measures (RF pulses) can be performed empirically for a given set of tissue parameters. For example, the number of RF pulses required to reach 95 % of steady-state spoiled GRE signal for myocardium (T1 = 1,000 ms, T2 = 45 ms), with a TR/TE/flip angle of 10/2/15°, is 87 RF pulses (87 × 10 ms = 870 ms). For a patient with normal sinus rhythm (60–70 bpm), this would be one heartbeat worth of dummy pulses [5].
Dummy heartbeats can be included at the start of an acquisition to drive the spoiled GRE signal to steady-state prior to data acquisition. This is realized in the example described above. In this case a single heartbeat of dummy RF pulses would be sufficient to reach 95 % of the steady state signal. The number of dummy heartbeats can be adjusted as well due to differences in tissue T1, flip angle, TR, and patient heart rate. The accepted steady state tolerance may be decreased (from 95 % above, to 85 %), to prevent increasing overall scan time.
SNR Considerations for Rapid Imaging
Some compromises become necessary to perform rapid clinical cardiac MRI, for example, sacrifices in SNR in order to acquire the necessary data in a timely manner. Most of the acceleration techniques have a similar goal: to decrease the number of phase-encoding lines (and hence, RF pulses) required to reliably reconstruct an image. Non-symmetric fields of view or matrix dimensions can reduce the number of phase encoding steps required with no inherent loss in SNR. However, acquiring only a portion of k-space, either through partial Fourier acquisition, or acceleration techniques such as GRAPPA or mSENSE, inherently alters the noise signature throughout the image and reduces SNR. Both of these techniques undersample the phase-encoding data during acquisition, and estimate the missing data during reconstruction. The resulting post-processed lines are created using these acquired lines. Therefore, the fewer true k-space lines acquired, the lower the overall SNR (reduced signal and increased noise).
Effect of Chemical Shift and Off-Resonance Effects
The Larmor frequency of a given H1 spin can be calculated empirically from the gyromagnetic ratio (γ) and the B0 field strength. However, H1 spins behave differently depending on their chemical environment. For example, the Larmor frequency commonly associated with H1 spins is calculated from water molecules. Chains of fatty acids have a different chemical environment, and hence a slightly different gyromagnetic ratio. This causes H1 spins in fat to resonate at a slightly different frequency from water (220 Hz at 1.5 T, 440 Hz at 3.0 T).
This can be imagined as two wheels spinning at slightly different rates. The signal received by the scanner is combined of spins in fat and in water, but the scanner expects to receive a signal at the water H1 Larmor frequency. Recall, frequency encoding gradient is used to record the excited spins from the imaged volume. If the H1 spins in fat are precessing at a slightly different frequency, they will be localized to a slightly different position, or “shifted” along the frequency-encoding direction (Fig. 10.4).


Fig. 10.4
MRI phantom showing chemical shift artifact (F fat, W water). With the frequency encoding direction from bottom to top, the fat tube (F) appears to be shifted 1–2 pixels higher than the water tubes. In reality, all tubes are in line
Obviously the mis-localization of fat can be problematic if it obscures anatomy, or worse, is confused with pathology (i.e. fat within the myocardium). Therefore, adjustments in receiver bandwidth can reduce the amount of chemical shift that occurs in an image. As an example, assume 1.5 T and a fat/water difference of 220 Hz. If our readout bandwidth is 220 Hz/pixel, then the fat will shift a full pixel in the frequency encoded direction, potentially confounding image interpretation. If the bandwidth were increased to 440 Hz, this shift would only be 0.5 pixels and the effect on image interpretation can be reduced [6].
Along the same lines as chemical shift artifacts, off-resonance effects can cause similar artifacts. In fact, chemical shift artifacts can be considered one specific type of off-resonance effect. In general, anything which causes a spin to precess at a resonant frequency which is different from its Larmor frequency can cause an off-resonance artifact. Off-resonance effects occur wherever a magnetic field gradient is present within the body. This could either be from intrinsic properties in the body (i.e. the “magnetizability” of tissue), or extrinsic sources such as eddy currents (produced from switching gradient coils on/off) or concomitant gradients (magnetic field changes orthogonal to applied magnetic field gradients). Overall, these effects result in a loss of signal in certain areas of the image due to a majority of H1 spins no longer precessing at the expected frequency. These can manifest themselves as spatial distortion (images appear warped), signal loss (at interfaces between tissue and lung), blurring, or overall signal heterogeneity (similar tissue appears bright or dark throughout the image) [7].
Parameter Selection (BW, FA/Ernst Angle, TE, TR, Scan Time, etc.)
When setting up a clinical cine CMR study, certain trade-offs come into play when optimizing spatial and temporal resolution, SNR, scan time, breath-hold capability, and overall image quality. As described below, the top requirement of cine MRI would be to capture the fastest phases of cardiac motion during contraction and relaxation of the ventricle. This requires high temporal resolution on the order of about 20 cine frames per cardiac cycle. If the temporal resolution is too low the tradeoff is missing peak systole causing an overall underestimation of ejection fraction, blurring of myocardium during cardiac motion, and inability to visualize wall motion abnormalities.
The required temporal resolution can be calculated by taking the patient’s average R-R interval, divide by 20 cine frames, and this produces the required temporal resolution. For example, a heart rate of 75 bpm is ~850 ms interval, if 20 cine frames are required, than the temporal resolution should be at least 42.5 ms. More details on setting optimal temporal resolution are included below.
Another way to optimize signal in a spoiled GRE image are to calculate the Ernst angle, which was described in Eq. 10.2 above. TE and TR need to be minimized in order to allow for increased imaging speed and reduction in breath-hold duration. Increasing the bandwidth can reduce the chemical shift artifact. The trade-off of increasing the bandwidth is a decrease in SNR. Finally, spatial resolution needs to be of a level where one can reliably delineate the border between the blood pool and myocardium, and the myocardial wall itself. Sacrificing spatial resolution for reduced scan time may limit the number of imaging voxels present across the myocardium, which may cause blurring of the myocardium during the most vigorous cardiac motion.
Balanced Steady-State Free Precession (bSSFP)
One method to overcome the limitations of spoiled GRE imaging is, instead of destroying transverse magnetization after each RF pulse, the magnetization can be “recycled” to increase SNR and image contrast between blood and myocardium. The approach, referred to as balanced steady state free precession (bSSFP) imaging, can be thought of as a hybrid of a GRE image and a spin-echo image. The RF pulses are played at a flip angle which oscillates from pulse to pulse, the spacing between RF pulses is double the echo time, and imaging gradients are perfectly matched between RF pulses. This results in magnetization that perfectly refocuses at each TE and eliminates the loss of signal seen in spoiled GRE imaging (Fig. 10.5) [8].
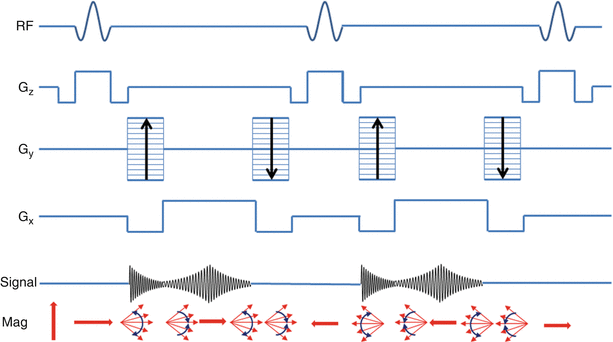

Fig. 10.5
bSSFP pulse sequence showing RF pulses, balanced gradients for slice encoding (Gz), phase encoding (Gy), and frequency encoding (Gx). Relative signal during each readout event (Signal), and resulting magnetization from each pulse sequence component (Mag)
bSSFP imaging has become the predominant cine imaging technique in most patients due to its high SNR, fast imaging speed, reduced flow dependency, and excellent blood to myocardium contrast. There are some caveats to these advantages. High flow velocity, metallic structures, and B0 inhomogeneities can cause severe artifacts in bSSFP imaging. Because the magnetization is refocused there is a “history” present with the H1 spins. Specifically, since spins are continually being refocused, if a spin is out of phase with other spins, the refocusing occurs at an arbitrary orientation, leading to signal loss. This is why artifacts from high velocity blood or metal implants are propagated through the image (see Video 10.1).
Signal Equation
The signal for a bSSFP sequence depends on sequence-selectable variables (TR, TE, and flip angle (α)), along with three variables intrinsic to the tissue being imaged (T1, T2, and M0). The steady-state equation for bSSFP signal is given in Eq. 10.3 below.
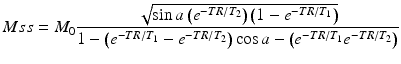 < div class='tao-gold-member'>
< div class='tao-gold-member'>




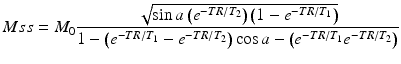
Only gold members can continue reading. Log In or Register to continue
Stay updated, free articles. Join our Telegram channel

Full access? Get Clinical Tree


