Risk stratification is a mainstay of current cardiovascular care. Its practical relevance to therapeutic decision making depends, however, on the often unverified assumption that higher risk patients experience greater treatment benefit. The truth of this assumption depends, in turn, on the particular set of variables in the putative risk prediction model, the pathophysiology of the underlying disease, and the associated goal(s) of therapy. If the operative set of risk predictors is incomplete (ignoring variables affected by treatment) or inconsistent (including variables unaffected by treatment), this will influence the relation between pretreatment risk and post-treatment benefit in complex ways having material clinical consequences. In conclusion, the clinical appropriateness of risk stratification must not be assumed. Instead, risk stratification guidelines specific to a particular disease and a particular treatment should be founded on prospective empiric validation.
Diseases desperate grownBy desperate appliance are relieved … — Hamlet (Act IV, Scene iii)
The thoughtful clinician takes it to be self-evident that the intensity of therapy should be proportionate to the risk of disease. Ever since Bigger coined the term “risk stratification” to characterize this intuitive process, the concept has become something of a mantra for rational, evidence-based clinical management, especially in the field of cardiovascular medicine, in which it plays a central role in a number of authoritative clinical practice guidelines. As a result, practitioners currently rely on risk prediction models for a pair of very different purposes: to predict clinical outcomes in individual patients and to predict the effects of treatment on those outcomes.
We previously described serious clinical limitations of the risk stratification paradigm stemming from its failure to account for the dynamic nature of clinical infirmity. Specifically, just as the physical trajectory of an object depends on its current magnitude of displacement with respect to time (velocity) and the instantaneous rate of change in that velocity (acceleration), the prognostic trajectory of a patient depends on the current level of infirmity with respect to time (risk) and on the instantaneous rate of change in that risk (hazard). Simply stated, one’s clinical course depends on how sick one is and how quickly one is getting better or worse. In this context, some therapeutic interventions (such as revascularization for ischemic heart disease) are directed more at the immediate mitigation of risk, while others (antithrombotic agents or statins) are directed more at the subsequent mitigation of hazard. These distinctions are central to the appliance of statistical prediction models to clinical practice–logistic regression versus Cox regression, for example.
From this perspective, risk assessment alone is an insufficient basis for therapeutic decision making. Instead, treatment is more appropriate, even when risk is low, if the hazard is positive (one is getting sicker), and treatment is less appropriate, even when risk is high, if the hazard is negative (one is getting better). In this essay, we extend this perspective to demonstrate several additional prerequisites of risk stratification relative to therapeutic management.
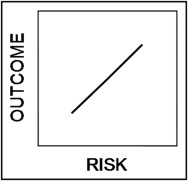
Let us begin by constructing a generalized model to predict the occurrence of adverse events associated with some putative clinical condition over a particular interval of time. Assume that there is a large set of empiric factors, {X}, that collectively predict the events and that we base our model on a conveniently small subset of these factors, {x}. For any patient, then, the model describes a complex relation between the observed frequency of an event (outcome) and its expected probability given the subset of factors (risk). If we are clever in our choice of the variables representing outcome and risk, we can make the relation between them perfectly linear, such that outcome = a × risk + b. This stereotypical risk prediction model is illustrated in Figure 1 .
The Global Registry of Acute Coronary Events (GRACE; http://www.outcomes-umassmed.org/grace/ ) and the Thrombolysis In Myocardial Infarction (TIMI; http://www.mdcalc.com/timi-risk-score-for-stemi ) scores, summarized in Table 1 , are well known examples of such risk prediction models. Both demonstrate similar performance (in terms of area under the receiver-operating characteristic curve and goodness of fit) in patients with ST-segment elevation myocardial infarction; the GRACE score is superior to the TIMI score, however, in patients with non–ST-segment elevation myocardial infarction patients.
| GRACE | TIMI |
|---|---|
| Age | Age |
| Heart rate | Diabetes/angina/hypertension |
| Blood pressure | Blood pressure |
| Serum creatinine | Killip class |
| Killip class | Body weight |
| Cardiac arrest | Anterior ST-segment elevation/left bundle branch block |
| ST-segment deviation | Time to treatment |
| Enzymes |
Models such as these have come to be widely used in clinical practice as a rational way to quantify prognostic risk, to justify the referral of higher risk patients to more aggressive treatment, and to assist in the elicitation of informed patient consent for such treatment. Current American College of Cardiology and American Heart Association practice guidelines thereby recommend early percutaneous coronary intervention in so-called high-risk ST-segment elevation myocardial infarction patients.
Recent observations, however, are inconsistent with the underlying premise that pretreatment risk implies post-treatment benefit. To confirm the validity of any such guideline, then, what we really need to know is the empiric relation between predicted risk and observed outcome in a stratified spectrum of patients with and without the treatment under consideration. As important as the quantitative assessment of risk might be for its own sake, and as useful as prediction models such as TIMI and GRACE might be for making these assessments, we cannot simply assume ipso facto that patients at higher risk necessarily experience greater therapeutic benefit. Figure 2 illustrates several alternative possibilities.
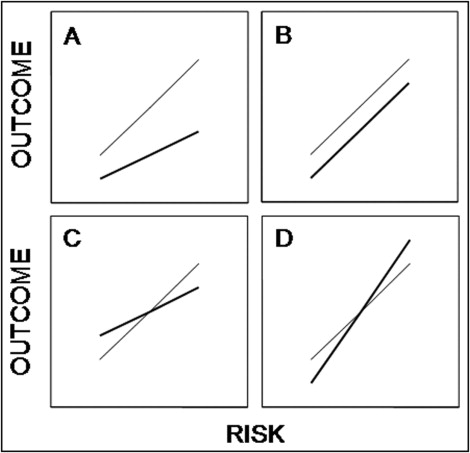
In Figure 2 A, post-treatment outcome at any magnitude of risk is improved relative to pretreatment outcome. Moreover, because the slope of the post-treatment risk curve is smaller than that for the pretreatment risk curve (a post < a pre ) and the intercept for the 2 relations is the same (b post = b pre ), the relative risk reduction associated with treatment is constant and independent of risk, while the absolute risk reduction increases as a linear function of risk. Thus, the greater the risk, the greater the treatment benefit, thereby justifying the use of this model for purposes of risk stratification and therapeutic decision making. It is generally agreed, for example, that the relative risk reduction associated with using statins for the prevention of cardiovascular events in stable patients is independent of rest levels of low-density lipoprotein cholesterol, a well-established predictor of risk. Accordingly, patients with higher levels of low-density lipoprotein cholesterol are considered more appropriate candidates for statin treatment than patients with lower levels. So far, so good.
Although we tend to think that this simple schema mirrors most of our treatment decisions, this need not be the case. In Figure 2 B, for example, things are very different. Although the relation between risk and outcome is positive before and after treatment, the slopes of the curves are now the same (a post = a pre ), causing the post-treatment curve to parallel the pretreatment curve, while the intercept of the post-treatment curve is smaller than that of the pretreatment curve (b post < b pre ). As a result, the absolute risk reduction is now constant over the entire range of risk, and the relative risk reduction actually decreases as risk increases. Such a model might be suited to risk stratification but not to tailored therapeutic decision making. Thus, because drug-eluting stents are associated with a finite risk for late stent thrombosis independent of baseline risk factors, current guidelines recommend that all patients receiving these stents be treated with prolonged antiplatelet agents, not just those at high risk.
To understand how similarly well validated models of risk prediction can lead to these confusing situations, we need to look more closely at the variables that make up the models. A variable that predicts risk need not predict therapeutic benefit. For the model represented in Figure 2 A, however, it stands to reason that one or another of the variables included in the subset {x} from which the model was constructed is improved by the treatment. In this case, for example, we might presume that our model includes a measure of ischemia as an index of risk and that our treatment is capable of relieving ischemia, thereby proportionately lowering the risk. For the model represented in Figure 2 B, treatment does not improve any of the variables included in the subset {x} but instead improves some other unmodeled variable making up the parent set {X} from which the subset {x} was derived. Such exclusions might occur because the critical unmodeled variable is, as yet, unrecognized or immeasurable.
Neither TIMI nor GRACE, for example, includes variables that might reasonably be considered to serve as proxies for the severity or extent of myocardial ischemia or the amount of blood flow in the culprit artery. Consequently, empiric models such as these might accurately quantify the magnitude of risk, but they cannot be expected to quantify the effect of any treatment directed at the restoration of flow or the relief of ischemia. If they do, it is only a matter of happenstance, not of design.
Even more complex relations can be expected if the treatment affects included and excluded variables in the risk model in opposite ways. Major interventions such as valve replacement surgery, cardiac transplantation, and defibrillator implantation might well evince such complex risk-benefit relations. In Figure 2 C, for example, treatment improves a variable included in the model (e.g., high-density lipoprotein cholesterol) but worsens a variable not included in the model (e.g., blood pressure). As a result, absolute and relative reductions in risk occur only above some threshold defined by the intersection of the pretreatment and post-treatment curves. In Figure 2 D, the opposite is the case. Treatment causes a variable included in the model to worsen but simultaneously causes a variable not included in the model to improve. Consequently, risk is reduced only below some threshold.
Is this all a needless pedantic exercise, or do such arcane situations really exist? To answer this question, just look back at Table 1 . Although GRACE and TIMI are well-validated and widely regarded risk stratification models, note that each includes variables not shared by the other (cardiac enzymes in GRACE and time to treatment in TIMI), and both include variables (such as age, serum creatinine, and body weight) that cannot be improved by the putative treatment (in this case, percutaneous coronary intervention). One might reasonably argue, in fact, that therapeutically irrelevant variables such as these should never be included in risk stratification models intended to guide treatment decisions, despite their independent statistical power. In this context, age would be appropriate for inclusion in a model used to select patients for surgical therapy, because it is a well-established determinant of operative risk, but would be inappropriate for inclusion in a model used to select patients for preventive medical therapy unless it is a proved determinant of therapeutic benefit.
Accordingly, variable selection is best guided by the underlying disease-specific pathophysiology and the patient-specific goal(s) of therapy. Consider coronary artery disease, as an example, for which we might choose to direct our therapeutic efforts in a given patient either at the atherosclerotic plaque (inflammation), the stenotic vessel (ischemia), impaired pump performance (heart failure), electrical dysfunction (arrhythmia), platelet aggregation (thrombosis) or some combination thereof. These 5 alternatives make for a total of 2 5 or 32 distinct therapeutic goals. Even the most sophisticated risk models cannot be expected to deal with such diversity. No wonder many of us rely instead on the predigested wisdom of packaged practice guidelines.
Even if we restrict ourselves, however, to a single therapeutic goal, and to a limited set of its most relevant predictors, differences from model to model will still persist. What are we to make of a pair of equally calibrated models when the first predicts high risk and the second predicts low risk in the very same patient (because some relevant predictor in the first model is abnormal while some other equally relevant predictor in the second model is normal)? Is there any rational basis by which we might choose either model over the other? Or should we simply average them together?
We were not able to identify the patient-by-patient correlation between TIMI and GRACE needed to answer these questions through a search of published medical research. We did, however, uncover a report by Lemeshow et al documenting the correlation between alternative models used to predict mortality in intensive care patients. Among 11,320 such patients, the calibration and discrimination of these alternative models were remarkably similar in the overall population, and more recent studies have shown them to be similar too in subgroups with cardiac disease and acute myocardial infarction. Nevertheless, the lack of agreement between the paired sets of predictions at the level of the individual patient was striking ( Figure 3 ) . Because the 2 models are so well calibrated, however, each of the discordant predictions remains equally valid conditioned on its attendant observations. In cases such as this, even the most sophisticated reclassification metrics are not likely to distinguish between them without consideration of additional factors such as cost and convenience. Likewise, alternative models for predicting mortality in patients referred for transcatheter aortic valve implantation show similar degrees of discordance at the patient level. Perhaps a combined model incorporating all the variables in each would perform better than either alone, but that too would require prospective validation. Other than practicality, then, there is no basis for preferring either model, or either prediction, over the other. As the saying goes, “You pays your money and you takes your choice.”





