Fig. 3.1
Schematic illustration of the principles governing the movement of ions through membranes. The membrane separating the two sides of the container is permeable to ion X+ but not to ion Y−. In the top row, where there are no impermeant ions, the steady state is a state of chemical and electrical equilibrium (as illustrated in the right panel). In contrast, when impermeant ions are present, as in the examples depicted in the bottom row, the steady state (as illustrated in the rightmost panel) is the condition at which the electrical gradient counterbalances the chemical gradient
If, instead, we also add an equal amount of negative ions (Y−) to which the membrane is not permeable, then we do not disturb the electrical equilibrium (since the net charge on either side is zero), but we create a chemical un-equilibrium for both types of ions (Fig. 3.1c). In this case, the positive ions will cross the membrane, forced by their concentration gradient, as before. In contrast, the negative ions, in spite an identical concentration gradient, will be unable to move because the membrane does not contain Y−-selective channels. The result would be the creation of an electrostatic imbalance, which was not present before, because there are now more negative charges on the left side of the membrane (Fig. 3.1d). The final steady-state of this system is depicted in Fig. 3.1e, where some of the permeant ions have moved back to the left side, so that the electrical un-equilibrium counterbalances the chemical un-equilibrium to create a resting steady-state.
Hence, it becomes evident that there are always two forces acting on the ions, one generated by the difference in concentration and the other by the difference in electrical charges across the two sides of the membrane. The electrical gradient (voltage) required to counterbalance the chemical gradient (concentration difference) resulting in a net flow = 0, is called the equilibrium potential for that particular ion and is described by the famous Nernst equation:
![$$ {\mathrm{E}}_{\mathrm{X}}=\mathrm{R}\mathrm{T}/\mathrm{z}\mathrm{F}\; \log {}_{\mathrm{e}}{\left[{\mathrm{X}}^{+}\right]}_{\mathrm{o}}/{\left[{\mathrm{X}}^{+}\right]}_{\mathrm{i}} $$](/wp-content/uploads/2016/07/A319559_1_En_3_Chapter_Equ1.gif)
Where R is the gas constant, T is the temperature in degrees Kelvin, z is the charge of the ion, and F is the Faraday (the amount of charge in coulombs carried my a mole of monovalent ions). For monovalent ions at room temperature (~20 °C), the Nernst equation is reduced to:
![$$ {\mathrm{E}}_{\mathrm{X}}=58\; \log {}_{10}{\left[{\mathrm{X}}^{+}\right]}_{\mathrm{o}}/{\left[{\mathrm{X}}^{+}\right]}_{\mathrm{i}} $$](/wp-content/uploads/2016/07/A319559_1_En_3_Chapter_Equ2.gif)
Hence, if we take the case of potassium ions (K+) as an example and we measure the K+ concentrations on both sides of the membrane, we can calculate that, for concentrations [K+]o = 5 and [K+]i = 140 nM, the equilibrium potential for K+, will be: 58 log10 5/140 = −84 mV. That means that if the membrane potential (Vm) is set at −84 mV (there are ways to do that experimentally, with the voltage-clamp method), there would be no net flow of K+ across the membrane. Or, in other words, potassium ions would be at equilibrium.
(3.1)
(3.2)
3.1.2 Resting Potential
The principles just discussed regarding the two forces (electrostatic and chemical) acting on the ions also apply in real cells, except that in this case there are multiple ions present, and real membranes have different permeabilities for the various ions. In the previous example with the hypothetical membrane, the unequal distribution of ions on the two sides was artificially imposed for the purpose of explaining the principles, and the membrane was either completely permeable to one type of ions (as in X+) or completely impermeable (as in Y−). In real cells the unequal distribution is created primarily (1) by the differential permeability of cell membranes for different types of ions (including the presence of non-permeant ions inside the cell); and secondarily (2) by the presence of energy-consuming ion pumps, or transporters.
1.
The differential permeability arises as a result of the presence of selective ion channels, i.e. specialized proteins that form aqueous pores across the membrane, through which specific ions can flow. Furthermore, as we shall see in the following section, the membrane permeability can change dramatically as a function of the membrane potential (Vm). At rest, the membrane exhibits high permeability to K+, i.e. many potassium channels are in an open state. In contrast, membranes at rest exhibit very low permeability to Na+ and Cl−, as most sodium and chloride channels are closed. The relationship between membrane potential and ionic concentrations is given by the Goldman-Hodgkin-Katz (GHK) equation:
![$$ {\mathrm{V}}_{\mathrm{m}}=\mathrm{R}\mathrm{T}/\mathrm{z}\mathrm{F}\; \log {}_{\mathrm{e}}\left[\left({\mathrm{K}}_{\mathrm{o}}+\left[{\mathrm{P}}_{\mathrm{Na}}/{\mathrm{P}}_{\mathrm{K}}\right]{\mathrm{Na}}_{\mathrm{o}}+\left[{\mathrm{P}}_{\mathrm{Cl}}/{\mathrm{P}}_{\mathrm{K}}\right]{\mathrm{Cl}}_{\mathrm{i}}\right)/\left({\mathrm{K}}_{\mathrm{i}}+\left[{\mathrm{P}}_{\mathrm{Na}}/{\mathrm{P}}_{\mathrm{K}}\right]{\mathrm{Na}}_{\mathrm{i}}+\left[{\mathrm{P}}_{\mathrm{Cl}}/{\mathrm{P}}_{\mathrm{K}}\right]{\mathrm{Cl}}_{\mathrm{o}}\right)\right] $$](/wp-content/uploads/2016/07/A319559_1_En_3_Chapter_Equ3.gif)
Therefore, the permeabilities (P) for each ion, in combination with the intracellular and extracellular ionic concentrations determine the final value of the membrane potential. There are, of course, other ions present besides the three just described (Na+, Cl−, and K+), but these are either present at very low concentrations, or there are no ion channels that permit them to cross the membrane. Hence, they contribute very little to the Vm and can be ignored for present purposes. Thus, when the Na+ and Cl− channels are closed, i.e. when PNa and PCl are close to zero, and the membrane is permeable only to potassium, the GHK equation reverts to the Nernst equation, as discussed before (Eq. 3.1).
( 3.3)
2.
Besides the passive flow along electrochemical gradients through ion channels, the membranes also contain energy-driven pumps or transporters, which use the energy from adenosine triphosphate (ATP) to overcome the barrier imposed by the lipophilic nature of the plasma membrane. Such pumps or transporters are proteins that physically grab ions from one side of the membrane and transport them to the other. These pumps are essential for the establishment of concentration gradients of various inorganic ions across the plasma membrane. Many of them are electroneutral, but some are electrogenic, i.e. they contribute to the membrane potential, since their activity results in a net flow of ions across the membrane. One such pump is the sodium-potassium pump, or Na+/K+ adenosine triphosphatase (ATPase), which transports three sodium ions out of the cell for every two potassium ions pumped in (Fig. 3.2). Hence, this specific pump helps to maintain the negative levels of the membrane potential [1].
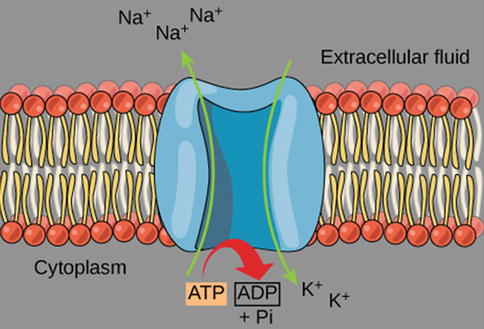
Fig. 3.2
Graphic illustration of the Na±-K± pump. The protein spans the plasma membrane of all animal cells and is an antiporter enzyme that pumps sodium out of cells, while pumping potassium into cells, against their concentration gradient using ATP as an energy source. The protein is a sodium dependent ATPase. Because the transport ratio is 2 K+ pumped in for 3Na+ pumped out, the Na+-K+ pump is an electrogenic antiporter, as it contributes to maintaining the negativity of the resting potential. An antiporter is a cotransporter and integral membrane protein involved in secondary active transport of two or more different molecules or ions across a phospholipid membrane, in opposite directions (Illustration reproduced with permission from: OpenStax College. ATP: Adenosine Triphosphate [OpenStax-CNX Web site]. 28 Jan 2013. Available at: http://cnx.org/content/m44427/1.3/)
This unequal distribution of charged particles on the intracellular and extracellular sides of the plasma membrane creates the voltage difference know as the “resting potential”. The resting potential, which in most cells is usually around −75 mV, can be viewed as a form of stored energy and lies at the basis of all cellular excitability. The resting potential is exactly large enough to balance the ion flow caused by the various permeant ions with their different concentration gradients and membrane permeabilities. At this voltage the net charge flow is zero and the membrane is at a resting steady-state, but not at equilibrium (Fig. 3.1e).
3.1.3 Action Potential
The plasma membrane of all excitable cells, including neurons and cardiac tissue, contains voltage-gated channels that are responsible for these cells’ non-linear response to depolarization and the generation of the AP. These channels can be in a closed or an open state, and the transition between the two is regulated in different ways (Fig. 3.3): in some channels the probability of opening is determined by the voltage difference across the membrane (voltage-gated channels), in others by the binding of a specific molecule on the channel (ligand-gated channels), and some may be activated by conformational change of the membrane itself (stretch-activated channels).
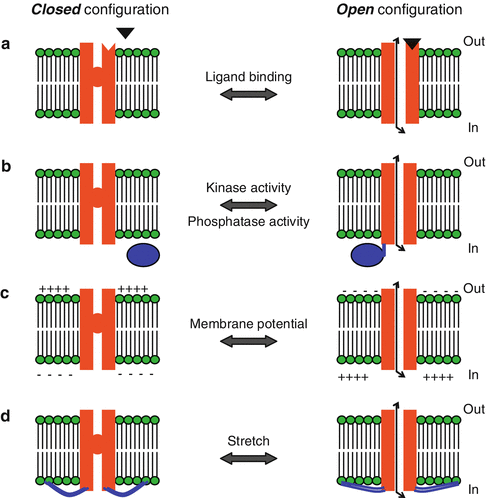
Fig. 3.3
Mechanisms of channel gating. (a) In ligand-gated channels, a molecule (black triangle) binds to the extracellular side of the channel protein and causes a conformational change that leads to channel opening. An example of a ligand-gated channel is the γ-aminobutyric acid (GABA)A receptor, where the binding of GABA on the channel leads to the opening of a Cl− channel. (b) Channel gating can also occur by phosphorylation or dephosphorylation of the channel protein, caused by the activity of kinases or phosphatases, respectively. (c) Gating in voltage-gated channels occurs through local changes in membrane potential, which lead to conformational change in the channel protein. (d) There are also channels that are activated by physical stretching of the membrane. In these, the channel protein is linked to the cytoskeleton (blue lines) and the gating is mechanical (Illustration modified with permission from: http://employees.csbsju.edu/)
The most important channels for the generation of the action potential are the voltage-gated channels, which open when the membrane potential reaches a certain value, and either remain open for as long as the voltage remains within a certain range, or close after a given time period (temporally regulated inactivation). All channels are selectively permeable to one or few types of ions and once open allow the specific ion(s) to move through it according to their electrochemical gradient, as described in the previous section.
To examine the sequence of events that leads to the generation of an AP we can refer to Fig. 3.4. At rest, the membrane potential is at a hyperpolarized level (−75 mV). This value may vary as it reflects the particular combination of ion channels present on the membrane, but is usually between −80 and −70 mV. When small hyperpolarizing stimuli are applied to the cell, the membrane potential becomes hyperpolarized to values below the resting potential (blue traces). When small depolarizing pulses are applied the membrane becomes depolarized accordingly (green traces). However, with a larger depolarizing pulse the membrane potential reaches the threshold level and a couple of action potentials are generated (red trace).
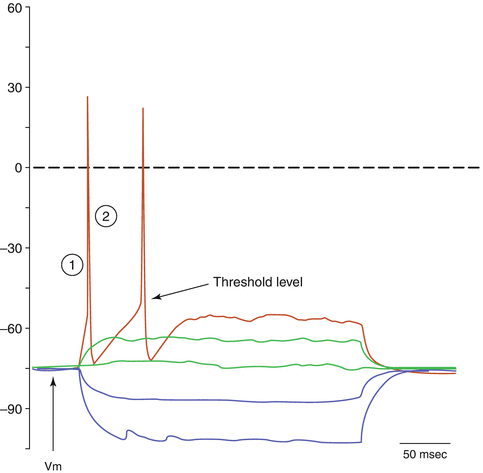
Fig. 3.4
Current-clamp whole cell recordings obtained from a cultured neuron. Three hundred millisecond-long hyperpolarizing and depolarizing current pulses are applied to the cell body and the change in membrane voltage is recorded. The resting potential is −75 mV
The upstroke of the action potential (indicated by circle-1 in Fig. 3.4) reflects the opening of the voltage-gated Na+ channels, which were almost completely closed at rest. Once open, the conductance for sodium ions is dramatically increased and Na+ rushes in, down its electrochemical gradient. This will cause further depolarization of the membrane, which will exceed the zero value and will tend towards the equilibrium potential for sodium (ENa = about +35 mV). The depolarization cannot exceed this level since at ENa, sodium ions are at electrochemical equilibrium and the net flow across the membrane will be zero – even if all Na+ channels were open. The reason that the depolarization does not quite reach the level of ENa is two-fold: (1) On one hand the voltage-gated sodium channels are temporally regulated and will have started to become inactivated, causing the conductance for Na+ to go back to resting levels and thus preventing further inflow. The inactivated state is different from the closed state, in that it is a state from which the channel cannot open. (2) At the same time K+ channels, which are also voltage sensitive but with slower kinetics, will have started to open and K+ will have started to move outwards along its concentration gradient, which is no longer counterbalanced by the electrical gradient as when the cell was at rest. The downstroke of the AP (indicated by circle-2 in Fig. 3.4) reflects the delayed opening of potassium channels and the outflow of K+ along its electrochemical gradient. After the return to baseline (or even below baseline in cells that exhibit an afterhypolarization) the cell will enter a refractory period, which is determined by the rate of recovery from inactivation of the Na+ channels. Until the termination of the (absolute) refractory period, no AP can be generated. The time course of the sequence of events that underlie the AP, and thus the duration of an individual AP, varies between cells. In most neurons and axons the entire sequence of events is over in a few milliseconds. In other cells, as in certain cells of the pituitary gland, APs may last for tens of milliseconds, whereas in cardiac muscle they can be hundreds of milliseconds long, as described in the next section.
3.2 Cardiac Conduction System
3.2.1 Electrical Properties of the Heart
The cells of the heart, like neurons or striated muscle fibers, are excitable and generate APs. The cardiac tissue consists of two types of muscle cells: (1) cells that initiate and conduct impulses; and (2) cells that, in addition to conducting impulses, respond to stimuli by contracting. Figure 3.5 illustrates APs found in different types of cardiac cells. Two types of impulses occur in the heart: the fast response AP occurs in atrial and ventricular myocardial cells; while the slow response AP occurs in (i) the sinoatrial (SA) node, which is the natural pacemaker region of the heart, and (ii) the atrioventricular (AV) node, which is the specialized tissue that conducts the cardiac impulse from the atria to the ventricles, but can also act as a pacemaker [2].
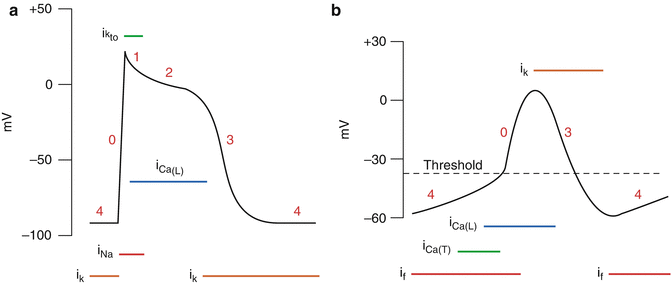
Fig. 3.5
(a) Fast response action potential, as found in ventricular myocytes. (b) Slow-response action potentials, as found in sinoatrial node cells (Illustration reproduced with permission from: www.cvphysiology.com)
As with most cells of the other tissues of the body (discussed in previous paragraphs), the intracellular K+ concentration of myocardial cells ([K+]i) exceeds the concentration outside the cell ([K+]o). The reverse gradient exists for Na+, Cl−, and Ca2+. Several types of potassium channels are present in cardiac muscle cell membranes [3], and the specific K+ channel which is active (i.e. open) at rest is the voltage-gated channel that conducts the inwardly rectifying K + current (IK i ). Inwardly rectifying potassium channels are a specific subset of potassium-selective ion channels. A channel that is “inwardly rectifying” is one that passes current (in this case potassium ions) more easily in the inward direction (into the cell) than in the outward direction (out of the cell). These channels, by mediating a small depolarizing K+ current at negative membrane potentials, help establish the resting membrane potential [4]. As for most cells, conductance for K+ (gK) in a resting myocardial cell is about 100 times higher than the conductance for Na+ (gNa).
3.2.1.1 Fast-Response Action Potentials
The characteristics of fast response APs are shown in Fig. 3.5a. When the cell is electrically stimulated (typically by a current from an adjacent cell), a sequence of events is set in motion, involving the influx and efflux of ions. When the resting membrane potential is depolarized to the threshold level of about −65 mV, the cell membrane properties change dramatically and Na+ enters into the myocardial cells through specific voltage-gated Na + channels (upstroke, depolarization, phase 0). The Na+ channels open very rapidly (in 0.1 msec), resulting in an abrupt increase of gNa. Once open, the Na+ channels inactivate and gNa rapidly decreases. The Na+ channels remain inactivated until the membrane begins to repolarize. Phase 0 is followed by a brief period of limited repolarization (phase 1) reflected in the notch between the end of the upstroke and the beginning of the plateau. This repolarization is the result of activation of a transient outward current carried mainly by potassium ions.
The plateau phase (phase 2) of the cardiac AP is sustained by a balance between inward movement of Ca2+ and outward movement of K+. Ca2+ enters in the cell via voltage-gated L-type Ca 2+ channels. These channels are activated when Vm reaches −20 mV and, like the sodium channels, inactivate slowly thus providing a long lasting Ca2+ inflow. Opening of Ca2+ channels results in an increase in Ca2+ conductance (gCa). Because [Ca2+] inside the cells is much less than outside, the increase of gCa promotes the influx of Ca2+ throughout the plateau. During the peak of the upstroke gK decreases (Fig. 3.5a), thus preventing the excessive loss of K+ during the plateau.
The process of final repolarization (phase 3) starts at the end of the plateau phase, when efflux of K+ from the myocardial cells begins to exceed Ca2+ influx, with several outward K+ channels contributing to the repolarization of the myocardial cell [5–7].
< div class='tao-gold-member'>
Only gold members can continue reading. Log In or Register to continue
Stay updated, free articles. Join our Telegram channel
Full access? Get Clinical Tree
